三相自励异步发电机稳态运行外特性的分析计算

尹小恩 周崐 贺天元

（海军驻湖南地区军事代表室，湖南 411101）

1 引言

异步电机发电时，需在定子出线端并联合适大小的电容同时要使发电机的转速不低于临界值。近年来，水能、风能、太阳能等绿色能源用作一次能源进行发电越来越多，在绿色能源充足的地区，采用异步发电机发电是一种可行的方案，这使得异步发电机的研究与应用得到重视[1]。

三相异步发电机带对称负载稳态运行时，发电机的自身参数值、机端并接自励电容值，所带负载大小和电机电压、电流、频率等物理量需要满足一定的平衡关系。对称稳态运行的分析计算通常是从折算到基值频率下的发电机等值电路出发，令等值电路回路阻抗或节点导纳为零、即它们的实部和虚部分别为零，联立方程求解[2-5]。

采用使等值电路的回路阻抗或者节点导纳为零的方法进行稳态分析时，因为回路阻抗或节点导纳表达式是所求变量5次以上的高次方程，对应的分析方法一般是 Newton-Raphson法[2,3]或优化计算方法[4]。Newton-Raphson法具有较高的精度与较快收敛速度，但在求解过程计算量大且稳定性差，初值选得不合适极易使迭代过程发散；优化计算方法编程和数值计算相对简单，但在优化过程中有可能找不到全局最优点而求不出方程的解。本文采用的迭代方法是一种简单实用的直接迭代计算方法，通过适当的方法降低方程的次数，使之针对2次方程而不是传统方法中5次以上方程，与文献[5]不同，本文使用回路阻抗分析法。在用新的方法分析异步发电机的外特性时，迭代过程中只需进行简单的计算，收敛速度快，且具有很好的通用性。考虑到异步发电机定子电流频率随负载的变化而变化，本文研究的外特性包含端电压随负载变化和定子电流频率随负载变化两条特性。

2 分析方法与迭代计算过程

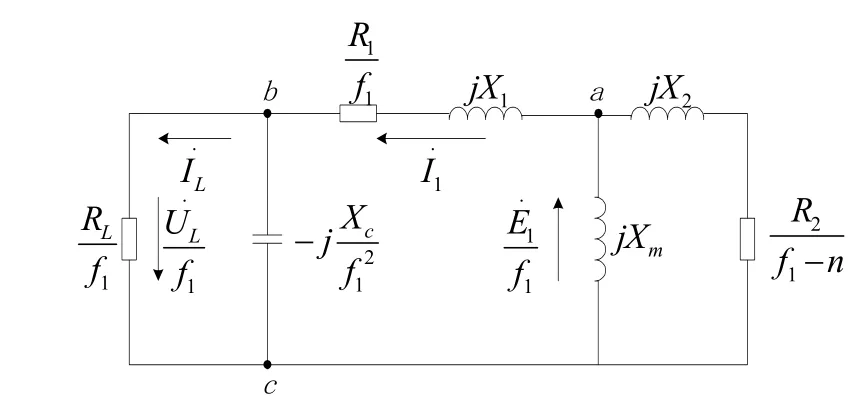
图1 异步发电机稳态运行等值电路

图1是异步发电机带电阻性负载稳态运行时折算到基值频率下的等值电路，其中各参数及变量均为标么值。为简化分析作如下的假设：

1) 除激磁电抗受饱和程度的影响以外，其它参数在迭代过程中均为常数；

2) 认为定、转子漏电抗相等；

3) 忽略铁心损耗的影响。

迭代方法以回路阻抗法为基础，由图1可得回路方程为

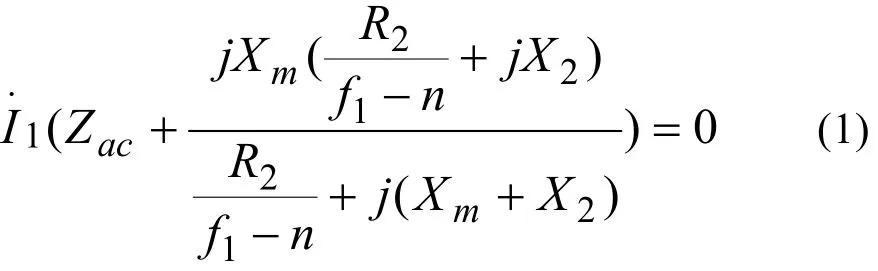
其中

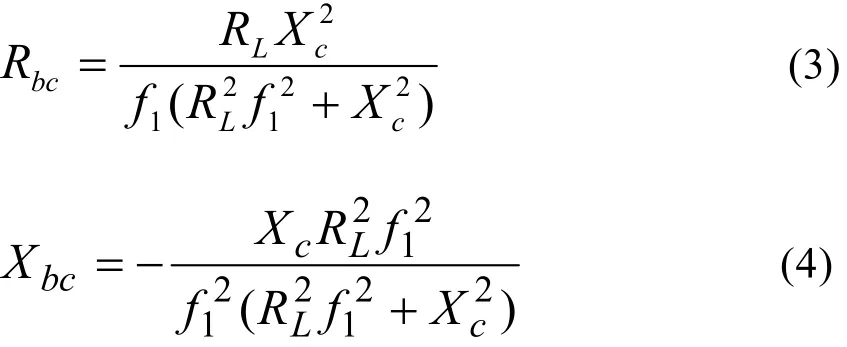
因为≠ 0，若使公式(1)成立，则有

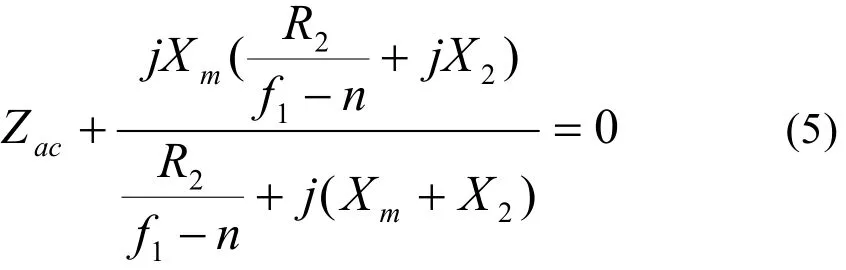
上式中阻抗为零对应其实部和虚部分别为零，即

把方程组(6)中的两个方程均化为激磁电抗 Xm的表达式

为分析方便，现定义异步发电机转差率为

把式(8)代入方程组(7)并消去激磁电抗得

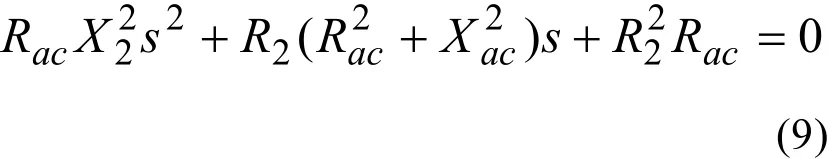
实际上，异步电机作为发电机稳态运行时的转差率为一个很小的负数，因而解式(9)得s的表达式

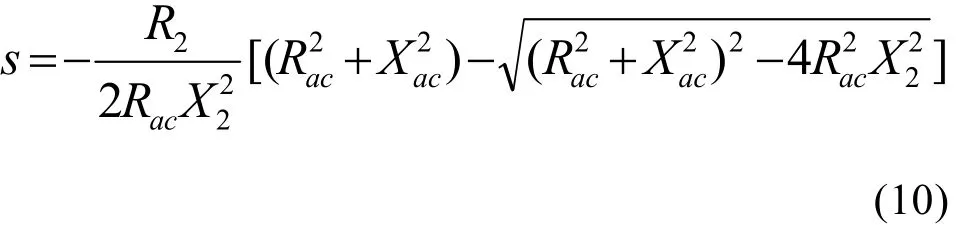
上式是转差率的表达式。由式(3)与(4)可知，Rac与Xzc随定子频率、即随转差率变化，若要根据式(11)得出转差率，必须通过迭代法求解。

迭代过程如下：

1) 给出频率 f1的初始迭代值，一般情况下取f10=n。

2) 用公式(3)、(4)计算 Rac、Xac。

3) 通过公式(11)求解 s，进而由公式(8)得到频率f1的值并作为下一次迭代初值。

4) 计算f1迭代值的增量，若增量小于一个足够小的规定常数ε，则迭代结束。

上述迭代过程只涉及到简单的计算，与传统的异步发电机稳态运行分析中所采用的牛顿-拉夫逊迭代法相比，编程与计算大大简单，且所编的程序具有很强的通用性。

现把迭代得到的f1、s代入公式(7)计算Xm，若 Xm小于未饱和值，即可由磁化曲线得到对应的E1。在给定转子转速n、自励电容容抗Xc和负载电阻RL，且电机其它参数已知的情况下，可根据图1的等值电路计算负载电流、机端电压、输出功率等，进而得到整个外特性。

3 计算结果与讨论

本文采用的样机为参考文献[2]中的电机，额定数据和参数如下：UN=230 V，IN=8.2 V，PN=2.2 kW，nN=1500 r/min，fb=50 Hz，p=2，定子边△接。计算过程电机参数中均采用标么值，R1=0.062，R2=0.07，X1=X2=0.093。

E1与 Xm的曲线通过同步实验测得，为线性化得到近似的关系为：

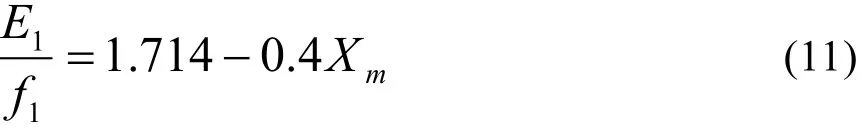
3.1 外接电容的影响

图2是在 n=1、电容值(实际值)分别等于44µF，50 µF，54 µF 时的一组外特性，其中电容等于50 µF时还给出了实验数据，实验数据同样取自参考文献[2]，试验数据与理论计算值的一致性说明了本文所采用分析方法的正确性。在输出功率相同的情况下，3条近似平行的实曲线说明端电压 UL与随电容值的增加而增加，而 3条在低输出功率区几乎重合的虚曲线说明电容值的变化对定子电流频率基本上没有影响。根据这些曲线还可以看出下面两点，一是随着电容值的增大，发电机的最大输出功率Pomax增加；二是在相同的UL下，电容值越大，输出功率Pout就越高。由于输出电流的限制使得当Pout增大到Pomax后，随着负载电阻的减小，UL迅速下降。进一步分析可知，提高自励电容值可以提高发电机的端电压和最大输出功率，但自励电容值不宜取得过大，否则自励电压会出现深度饱和的现象，励磁电流太大，铁耗大增而使电机运行效率下降。

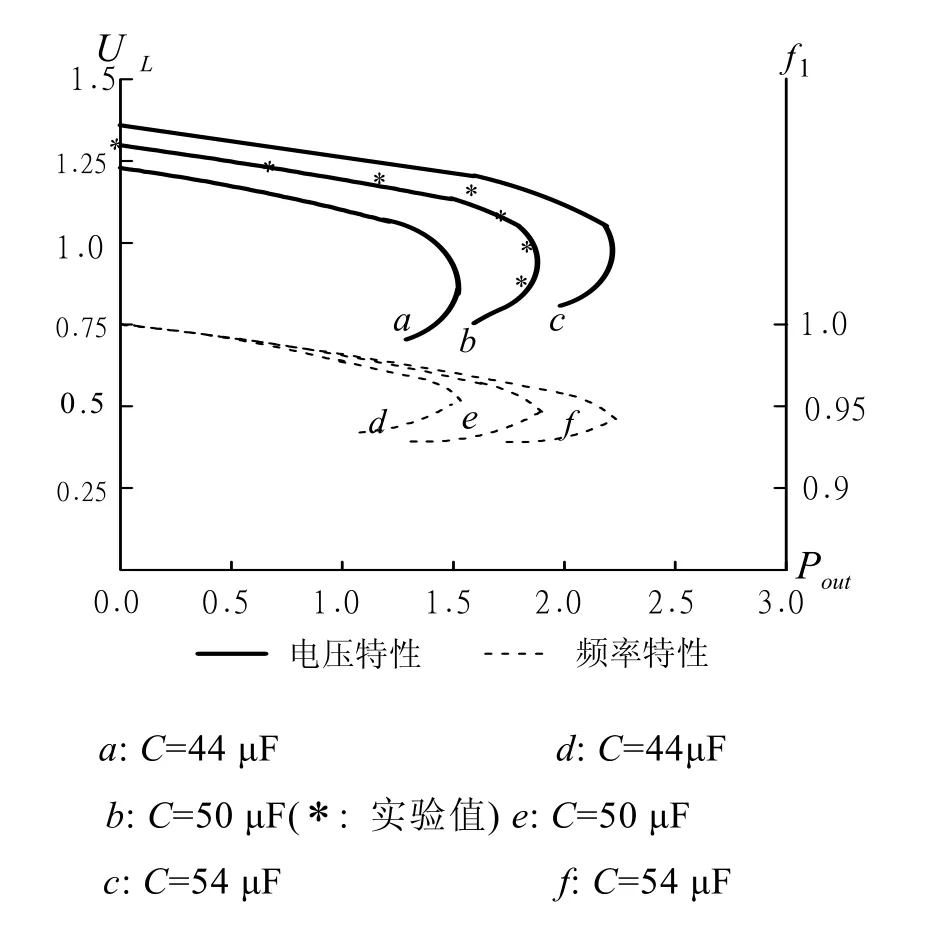
图2 外接电容对外特性的影响

3.2 转速的影响

在C＝50 µF，转子转速为基值转速k倍时，图3中给出了转速对外特性影响的曲线。从图3中看出，在相同输出功率情况下，UL和f1几乎与转速成比例增加，但端电压变化范围大，而频率变化范围小，所以说转速是对外特性影响较大的一个量。

图3 转速的影响

4 结论

本文采用了迭代的方法进行了外特性的计算，该方法的计算机算法编程简单且具有一定的通用性。在给定的励磁电容、转速和负载下，通过计算激磁电抗与输出频率，进而得到整个外特性。迭代过程只需进行简单的代数计算，在保持很高精度的情况下，一般只需几步即可得到所需的结果。

多组曲线表示了不同参数对于外特性的影响。励磁电容、转速的增加（或减少）会使相同负载下的输出电压显著的增加（或减少），电容、转速、转子电阻是对频率变化敏感的参数。

：

[1]杨顺昌. 笼型感应电动发电机的应用前景及电磁设计特点. 电工技术学报, 1994, 9(3): 11-14.

[2]S. S. Murthy, O. P. Malik, A. K. Tandon. Analysis of self-excited induction generators. IEE Proc., Pt. C.1982, 129(6): 260-265.

[3]李光友, 王建民, 孟传富, 等. 利用并串联电容自励恒压的异步发电机及其分析. 电工电能新技术,1997, (4): 53-56.

[4]Alolah A L, Alkanhal M A. Optimization-based steady state analysis of three-phase self-excited induction generator. IEEE Trans. on EC, 2000, 15(1): 61-65.

[5]T. F. Chan. Analysis of self-excited induction generators using an iterative method. IEEE Trans. on EC, 1995,10(3): 502-507.