基于动力论的尘埃等离子体充电方程研究
陈惠敏 石雁祥 苏金善 孙 毅 张保花
(1.昌吉学院物理系,新疆 昌吉831100;2.伊犁师范学院物理与电子信息学院,新疆伊宁835000)
1.引 言
尘埃等离子体可简单定义为在一般等离子体中考虑尘埃粒子作用的等离子体。
尘埃等离子体理论是20世纪80~90年代在国际上出现的一门新型理论。它建立在一般等离子体理论基础上但考虑了尘埃粒子的作用。由于在天体物理、航空航天、大气环境、微波通信、微电子器件制造等一些重要的科学技术领域存在着与尘埃等离子体有关的问题,尘埃等离子体理论及相关的应用研究开始受到越来越普遍的重视。
尘埃等离子体与一般等离子体最大的不同在于尘埃粒子的充放电作用。并由此导致尘埃等离子体的很多物理性质与一般等离子体不同。尘埃粒子充电方程是描述尘埃等离子体充放过程的基本方程。而充电频率(电荷驰豫速率)是描述这一物理过程的基本物理量。有关尘埃粒子充电问题的研究已经发表了多篇文献[1-11]。其中,Jana和 Tsytovich分别根据各自不同的方法给出了充电频率的两种不同表达式[1,2]。在研究尘埃等离子体微波散射及尘埃等离子体中各种纵波问题时,不同的文献引入了不同的充电频率表达式。然而,对两种表达式之间的关系至今尚没有给出明确的说明。本文在动力论基础上研究尘埃粒子充电问题,导出尘埃粒子充电方程,给出了充电频率表达式。证明了两种充电频率表达式是考虑不同近似条件得到的。
2.理论分析
2.1 尘埃粒子充电电流的OLM理论
我们考虑浸在非磁化电子—离子等离子体中的有限尺寸的尘埃粒子。因为电子的热速度远大于离子的热速度,电子到达尘埃粒子表面比离子快。因此,尘埃粒子获得的电子比离子多很多,结果它的表面电势变成负值。当然,原来的电子电流和离子电流会受尘埃粒子表面电势的影响,因为它们依赖等离子体和尘埃粒子的相对速度。当表面电势是负的时候,电子就会被排斥而离子被吸引,即由电子携带的尘埃粒子电流降低而由离子携带的尘埃粒子电流增加。
采用轨道受限运动(the orbit-limited motion,OLM)方法来计算等离子体粒子j(电子或离子)对尘埃粒子的充电电流Ij。考虑等离子j体粒子从无限远的距离接近半径为rd带电量为qd的尘埃粒子的情况,如图1。当带电粒子进入德拜球时,它会受到尘埃粒子的影响,由于库仑电场的作用,它的路径会发生变化。假设Vj和Vjg分别是等离子体粒子与尘埃粒子刚好擦过时前后的速度,显然,对于一个确定的速度,小于碰撞参数bj时,等离子j体粒子j就会与尘埃粒子相碰。其充电碰撞的碰撞截面是=。
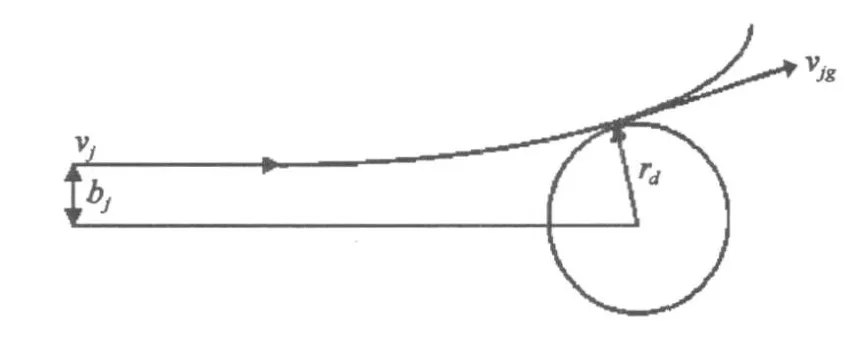
图1 等离子体粒子j与带电尘埃粒子之间的摩擦碰撞(qj<0,qd<0)
由于带电粒子受有心力作用,角动量和能量守恒定律要求
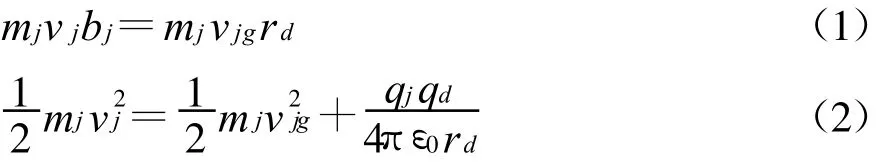
尘埃粒子的带电量qd=Cφd,φd=φg-φp是尘埃粒子势φg与等离子体势φp之间的电势差。在等离子体中,球形尘埃粒子的电容C=rdexp(-rd/λD)。对于德拜半径λd≫rd的情况,C≈rd。联立求解(1)式和(2)式并考虑到关系式qd=rdφd可以得到

若距尘埃粒子为无限远的等离子体粒子j的速度分布是fj(vj),则由j类等离子体粒子产生的尘埃充电电流Ij是

式中,Vjmin是与尘埃粒子碰撞的等离子体粒子的最小速度。Vjmin的值可分两种情况讨论:当qiφd<0时,等离子体粒子和尘埃粒子相互吸引,Vjmin=0;而当qjφd>0时,等离子体粒子和尘埃粒子由于库仑力作用而相互排斥,只有那些动能大于相互作用势能的充电粒子才能接近尘埃粒子而对其充电,在这种情况下Vjmin可表示为[6]
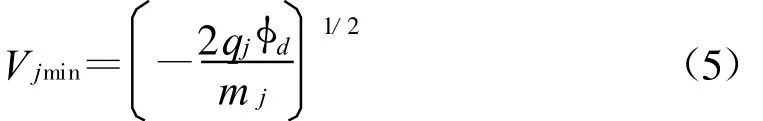
进一步假设等离子体粒子的速度分布服从Maxwell分布,即[12]

式中,nj是等离子体粒子浓度。把式(5)、(6)代入式(4),用球坐标表示并进行积分可以得到充电电流为
当qjφd<0 时 ,当qjφd>0 时 ,
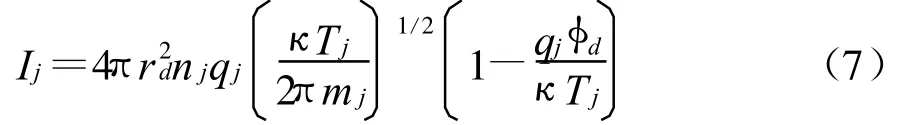
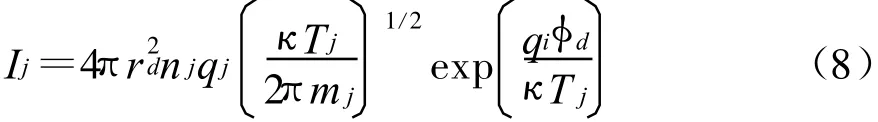
2.2 充电平衡条件和电中性条件
当粒子停止充电并达到稳定状态时的尘埃粒子表面电势称为平衡电势。尘埃粒子的充电平衡电势可由充电平衡条件和准中性条件得到。若已知尘埃粒子的半径,进一步还可得到尘埃粒子的带电量。
由于离子质量远大于电子质量,离子的热运动速度要远小于电子的热运动速度,因而,在充电过程初期,离子的充电电流Ii要远小于电子的充电电流Ie,充电使尘埃粒子带上了负电。由于尘埃粒子表面带负电,对于电子qjφd>0;对于离子qiφd<0,由式(7)和式(8)可知,电子和离子的充电电流分别可写为

假定了离子是一次电离的,即对于离子qj=e(e=1.6×10-19C)。随着充电的继续,带负电的尘埃粒子开始排斥电子同时吸引离子,这使得离子的充电电流开始增加,电子的充电电流开始减小。当Ii=Ie时,尘埃粒子处于充电平衡状态。在多种带电粒子对尘埃粒子充电的情形,充电平衡条件可以写为

由于尘埃粒子的带电,尘埃等离子体的电中性条件与一般等离子体不同,其表现形式为ne+Zd nd=ni,即

式中:Zd是尘埃粒子电荷数;nd是尘埃粒子浓度。当Zd nd/ni≪1,尘埃粒子是孤立的,此时ni≈ne。随着尘埃粒子浓度增大,尘埃粒子间距减小,尘埃粒子之间的库仑相互作用将会逐渐增大,当Zdnd/ni与1可以比拟时,尘埃粒子不能被看作是孤立的。对于非孤立尘埃粒子,其表面电势φg与等离子体电势φp之差小于孤立尘埃粒子时的情形,因此其尘埃粒子的电量也小于孤立尘埃时的情形。这是由于当尘埃粒子增多时,虽然尘埃粒子总体会占有更多的电子,但每个尘埃粒子分得的电子却会减少。
3.理论推导
3.1 尘埃粒子充电方程
在电子和离子对尘埃粒子充电的过程中,由于受到尘埃等离子体中纵波的影响,充电电流也会产生波动,结果会引起尘埃粒子表面电量的起伏。假定不存在波动时,尘埃粒子带电量的平衡值为qd0,则纵波的影响使尘埃粒子带电量围绕qd0起伏,表示为qd0+qd1,qd1是尘埃粒子受纵波影响产生的电量起伏值,qd1远小于qd0。充电频率νch描述了尘埃粒子表面电量恢复到平衡值时的快慢程度。对于由电子﹑一次电离的离子以及尘埃粒子组成的尘埃等离子体,充电平衡时,由充电平衡条件式可得
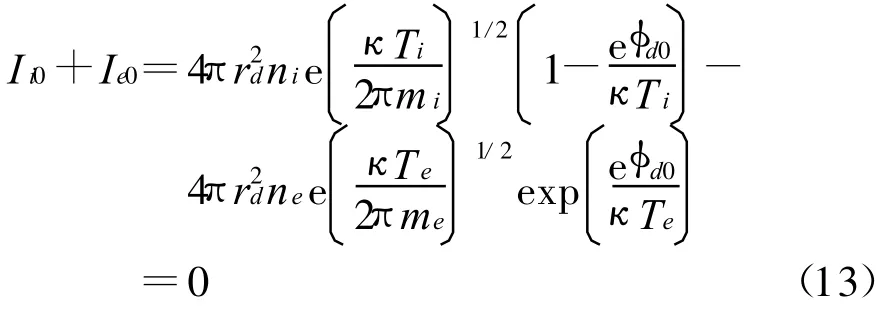
用|Ie0|表示充电平衡时电子和离子的充电电流,则

有纵波存在时等离子体j粒子的分布函数为

fj0是未受扰动时j粒子的分布函数。fj1表示分布函数的微扰。
纵波存在时的充电截面为
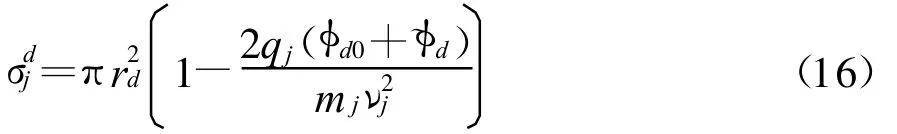
式中:φd0是充电平衡时的尘埃粒子电势与等离子体背景电势之差;˜φd是围绕平衡电势变化的浮动电势。于是,有扰动时的充电电流为

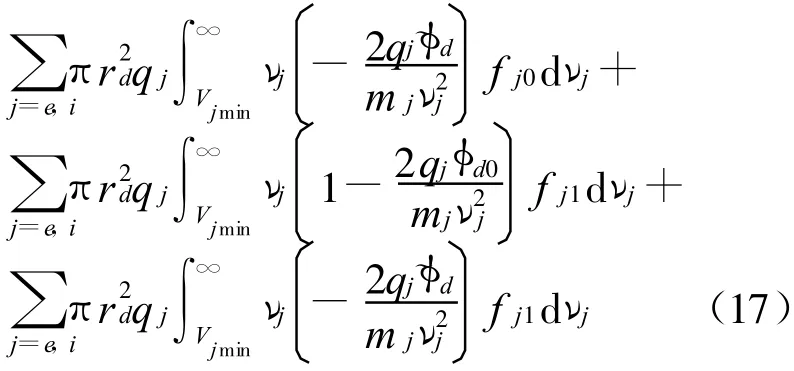
式中
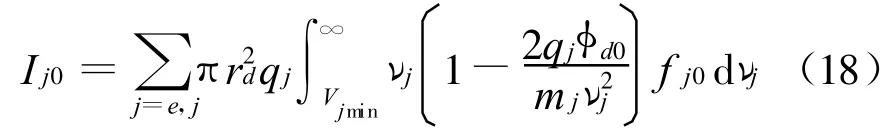
为没有扰动时的充电电流。式(17)其余三项分别代表充电截面变化、分布函数变化对扰动电流的贡献,以及充电截面变化及分布函数变化共同引起的扰动电流。
3.2 尘埃粒子的充电频率
考虑到fα1≪fα0,φd≪φd0,式(17)等式右边最后一项为二阶小量,可以忽略。于是

式中
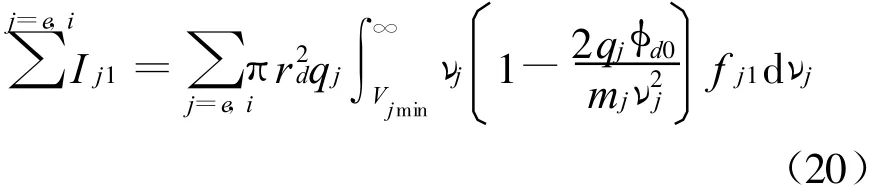
代表分布函数变化对扰动电流的贡献。
在忽略尘埃粒子运动速度的情形下,尘埃电量qd与充电电流的关系为

将尘埃粒子电量写为qd=qd0+qd1。qd0为充电平衡时的尘埃电量,它不随时间发生变化。将式(19)代入式(21),并考虑式(13)得

式(22)右端第二项的求和包括电子e和离子i。以下讨论式(22)右边积分,将式(6)代入该积分可得
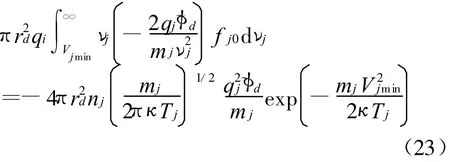
对于电子,将=代入上式
得
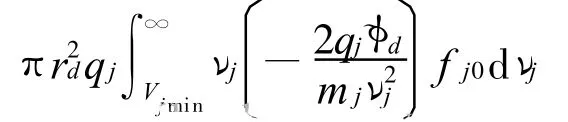

对于离子,qjφd<0,将Vjmin=0代入式(23)得
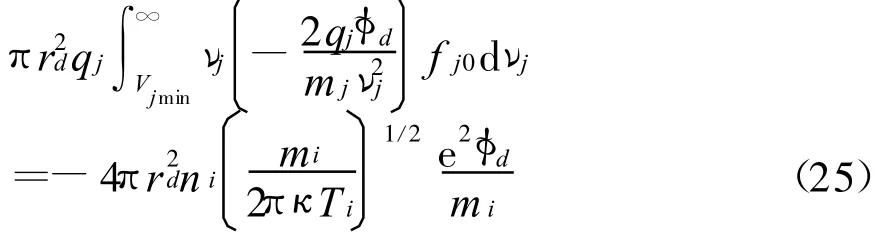
考虑到式(14),可得
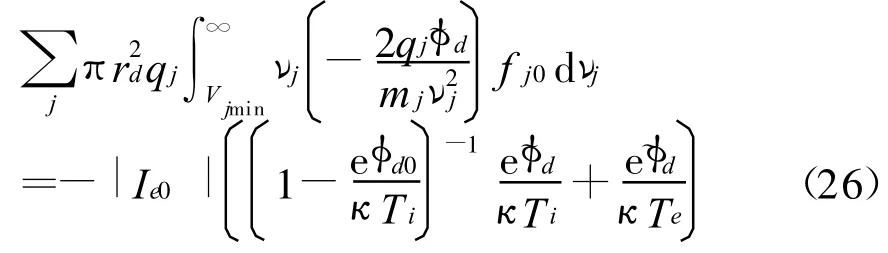
设尘埃粒子电容为C,则,将式(26)代入式(22)得

式中,νch是充电频率[2],在一些文献里也被称为电荷弛豫速率[8-11]
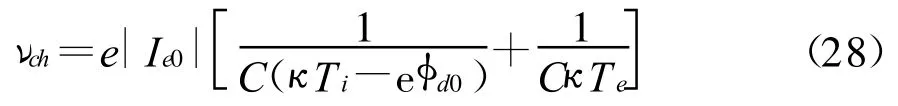
通常也将式(27)写为

式(29)即为充电方程的常见形式[8]。
假设尘埃粒子带负电,并设电荷数为Z,则φd0=-Ze2/rd,将式(14)|Ie0|的具体形式代入式(28),得
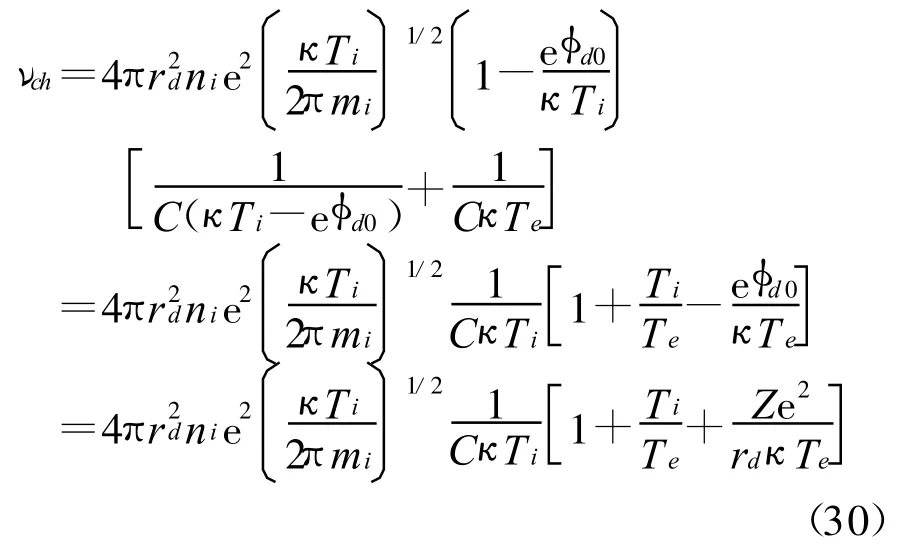

这正是文献[2]给出的结果。式(28)和式(31)常出现在以往的文献中,但各种文献对两者的关系没有做出说明,这里给出进一步的说明。
4.结 论
尘埃等离子体与等离子体最大的不同在于尘埃粒子的充电作用。在动力论基础上推导尘埃粒子充电方程,给出的充电频率具有统一形式表达式,文献中给出的两种不同形式的充电频率是在不同近似条件下给出的。
[1] JANA M R,SEN A,KAW P K,et al.Collective effects due to charge-fluctuation dynamics in a dusty plasma[J].Phys.Rev.E,1993,48(4):3930-3933.
[2] TSYTOVICH V N,HAVNES O.Charging processes,Dispersion properties and anomalous transport in dusty plasma[J].Comments Plasma Phys.Controlled Fusion,1993,15(5):267-280.
[3] HAVNEs O.Charges on dust particles[J].Adv.Space Res.,1984,4(9):75-83.
[4] GOREE J.Ion trapping by a charged dust grain in a plasma[J].Phys.Rev.Lett.,1992,69(2):277-280.
[5] ALLEN J E.Probe theory-theorbital motion approach[J].Phys.Scr.,1992,45:497-503.
[6] MA J X,YU M Y.Langmuir wave instability in a dusty plasma[J].Phys.Rev.E,1994,50:2431-2433.
[7] BARKAN A,D'ANGELO N,MERLINO R L,et al.Charging of dust grains in a plasma[J].Phys.Rev.Lett.,1994,73(23):3093-3096.
[8] SHUKLA P K,MAMUN A A,Introduction to dusty plasma physics[M].London:IOP Publishing Ltd,2002.
[9] 石雁祥,葛德彪,吴 健.环境压强对固体火箭喷焰电导率的影响[J].电波科学学报,2008,23(6):1115-1118.SHI Yanxiang,GE Debiao,WU Jian.Influence of pressure of environment on conductivity of solid rocket exhaust plume[J].Chinese Journal of Radio Science,2008,23(6):1115-1118.(in Chinese)
[10] 薛 昆,郭立新,吴 健,等.高纬极区电离层离子速度分布函数的多项式解[J].电波科学学报,2009,24(5):813-819.XUE Kun,GUO Lixin,WU Jian,et al.The polynomial solutions of the ion velocity distributions in the high-latitude auroral ionosphere[J].Chinese Journal of Radio Science,2009,24(5):813-819.(in Chinese)
[11] 石雁祥,王 菊,吴 健,等.对两种弱电离尘埃等离子体特征参量的定量估计[J].电波科学学报,2008,23(1):95-99.SHI Yanxiang,WANG Ju,WU Jian,et al.Characteristic parameters estimation of two weakly ionized dusty plasma[J].Chinese Journal of Radio Science,2009,24(5):813-819.(in Chinese)
[12] ALEXANDROV A F,BOGDANKEVICH L S,RUKHADZE A A,et al.Principles of Plasma Electrodynamics[M].Berlin:Springer,1984:59.

