基于改进物理光学法的电大目标双站RCS的预估
陈博韬 雷振亚 谢拥军2, 李晓峰 满铭远
(1.西安电子科技大学天线与微波技术国家重点实验室,陕西西安710071;2.北京航空航天大学电磁兼容实验室,北京100083)
1.引 言
随着隐身与反隐身技术的不断发展,谋求武器装备的隐身化已成为军事高新技术的热点之一。飞行器雷达隐身技术可显著降低敌方的探测概率,大幅提高飞行器隐蔽突防的能力和作战效能。目前隐身技术发展,对于飞行器目标单站散射特性分析和单站隐身布局设计是成熟有效的[1]。但是随着隐身与反隐身研究的深入,单站雷达的缺陷越来越突出,利用雷达组网来准确地发现目标成为发展的必然趋势,寻求一种准确快速的计算双站RCS的方法成为当务之急。
近年来,国内外学者纷纷采用各种不同的算法对复杂电大目标的双站电磁特性进行分析。有些学者采用了矩量法(MOM)与有限元(FEM)等低频方法,用以解决电大尺寸目标的双站散射问题,但是受到计算机内存过大及计算时间过长的限制。由于以上限制,出现了新型迭代推进方法[2-4]用于求解电大目标双站散射问题。时域场的迭代递推方法[2]和电流的迭代递推方法(CMT)[3],由于离散空间网格数量巨大和前、后向电流迭代时间需求较长的限制,并不适用于电大尺寸目标的求解;而空间场的迭代递推方法[4]虽然对于处理大角度问题的精确性更高,但在边界条件上的处理较为复杂,尤其在计算三维散射时引入的计算复杂度较高,另外计算时间与低频算法相比时间虽有所减少,其实时性还是难以实现;矩量法和物理光学法(PO)的混合方法处理目标单站RCS时比较有效,但是计算双站散射需要考虑电大尺寸的阴影面,仍然会存在内存和时间的限制[5];Crispin等学者利用单双站等效原理[6],结合图形电磁计算方法进行了双站RCS的计算,但是单双站等效原理仅仅在双站角远小于π的情况下是基本正确的,当双站角接近π时,该理论明显是错误的;另外有些学者则利用多边形面元的双站散射进行计算[7],由于只考虑了照明区域的电流贡献,而忽略了阴影区电流的贡献,同样导致了当双站角增大时,计算结果误差有所增大。因此,复杂电大目标的双站RCS计算虽已取得了初步成果[8-9],但在理论方法和试验方面都需要大力发展,尤其在大角度双站情况下缺乏有效的计算方法。
本文研究了电大目标双站RCS的改进物理光学方法。针对以往双站高频算法由于忽略阴影区电流影响,导致大双站角下计算误差有所增大的问题,提取电流步进法中的迭代算子,考虑阴影区面元间的耦合影响,对阴影面电流进行准确计算。与图形电磁计算方法相结合,推导出了改进的物理光学公式。对照明区,采用物理光学近似进行求解;对阴影区面元,按照入射波方向进行排序迭代求解,从而能够在考虑阴影面电流影响的基础上,快速有效地计算电大目标的双站RCS.
2.理论分析
考虑位于自由空间环境中的电大导体目标,如图1所示,S为导体目标表面,Ei是入射电场,由入射平面波将导体目标分为光照区和阴影区。

图1 目标双站修正计算模型
当处理复杂电大目标的双站RCS计算时,低频算法对计算内存和时间的需求已经远远超出现有一般计算机的计算能力。综合考虑计算效率、准确性和阴影面电流影响等因素,在利用电流步进法对阴影面电流进行准确计算的前提下,将它与高频算法相互结合进行计算分析还是合理的,可将总散射场表示为如下两类散射场的叠加:

2.1 图形数据实时预处理
在本文引入电流步进法计算复杂目标阴影区面元的电流值,并与图形电磁学相结合[10],对光照区的面元散射进行计算。因此,需预先对目标的阴影区、光照区面元进行划分,提取目标的几何信息进行存储[11],并对面元按照入射波的方向进行排序。
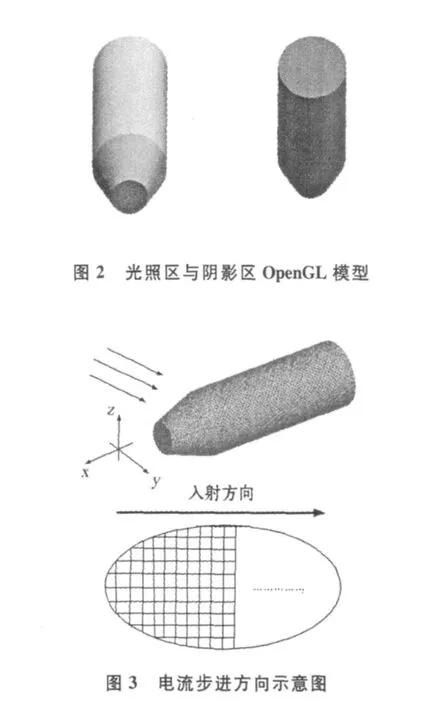
通过三维图形软件标准接口OpenGL来拟合电大导体的外形,采用硬件加速卡对目标以及背景象素进行显示,并实现自动消隐。按照像素的分辨率对面元进行剖分,同时利用光照模型实现导体目标的着色渲染,如图2所示。利用双缓存技术,可以对光照区和阴影区的面元的法矢量和深度缓存等几何信息进行实时读取,并利用深度缓存对面元按照入射波方向进行先后排序。
2.2 光照区面元的双站散射
当导体目标长度满足L>>λ时,可以将其作为众多独立的散射中心的叠加,利用物理光学方法来计算散射电场。在光照区金属体表面上,电流密度J满足的边界条件可以写为

对于面元部分,采用物理光学法进行分析,在得到表面感应电流后,用远区辐射积分来求解散射电场Es
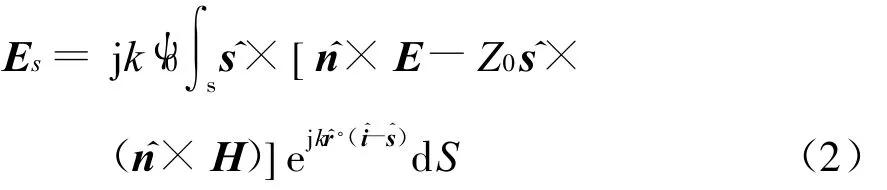
将远场边界条件代入式(2)中,可得到化简后的远区散射场为

式中:Ei0为入射电场强度;为多边形表面外法向单位矢量为入射磁场极化方向矢量。
式(3)中的积分在照明面∑上进行,当面元足够小时,其在屏幕上图象显示为一个象素,可以利用图形技术来依次提取像素的法矢量信息,对整个目标光照区的N个像素进行积分,就能够得到光照区的总散射场Esl

2.3 阴影区面元的双站散射
针对高频区复杂电大目标的阴影面,本文采用了图形电磁算法与电流步进法相结合的方法,来对阴影区的面元散射进行计算。电流步进法[3]是把严格的磁场积分方程进行前向/后向迭代求解并给出目标表面电流分布的一种方法。在初次前向步进过程中,每个面元上的原始电流设为零,每次计算一个面元上的电流,并将前面面元的结果代入后面面元的计算,直至最后一个面元,这样完成一次前向步进过程。在以后的步进过程中,面元上的原始电流是前面步进过程的计算结果。这种方法收敛的速度相当快,只需为数不多的迭代次数便可以使表面电流收敛至期望值。由电流步进法可以得到,在入射平面波激励下,散射体表面电流密度为

在高频区,目标光照区域的电流主要是由平面照射波的激励项引起的,阴影区域的面元电流主要是由光照面的电流耦合影响产生的。在传统的高频计算方法中,常常忽略阴影面的影响。虽然阴影区的电流非常小,但是在某些应用中它们对于散射的贡献是不可忽略的。在这种情况下,我们利用图形电磁学计算光照区的像素表面电流,之后提取电流步进法中的耦合项,用于计算阴影区面元在光照区耦合影响下的电流值。这样可以在利用电流步进法对阴影面电流进行准确迭代计算的同时,结合高频算法的优点,有效避免对整体目标花费大量的内存和时间进行求解。目标光照区的电流密度J已通过物理光学法得到,阴影区面元初始值设为零,然后按照入射波的方向排序进行迭代计算。根据式(5),阴影区面元的电流密度表达式可以写为

通过连续的前向/后向迭代直到收敛,得到阴影区面元电流值后,代入远区散射场公式(2)中,得到阴影区散射场Esd,复杂目标的双站 RCS可以表示为N个光照区面元散射场Esl与M个阴影区面元散射场Esd的叠加[12]
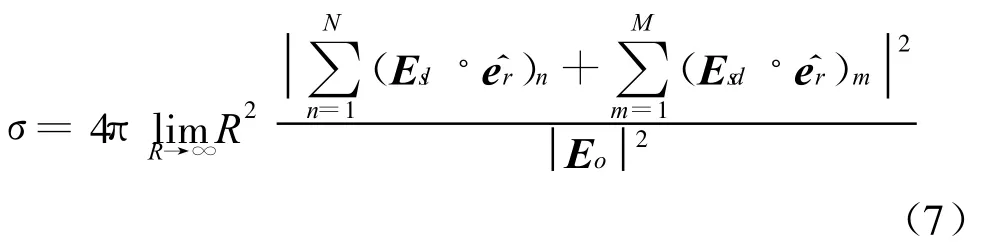
式中:σ表示复杂目标的RCS;R是从雷达到该散射中心的双程距离是接受装置电极化方向的单位矢量。
3.计算实例
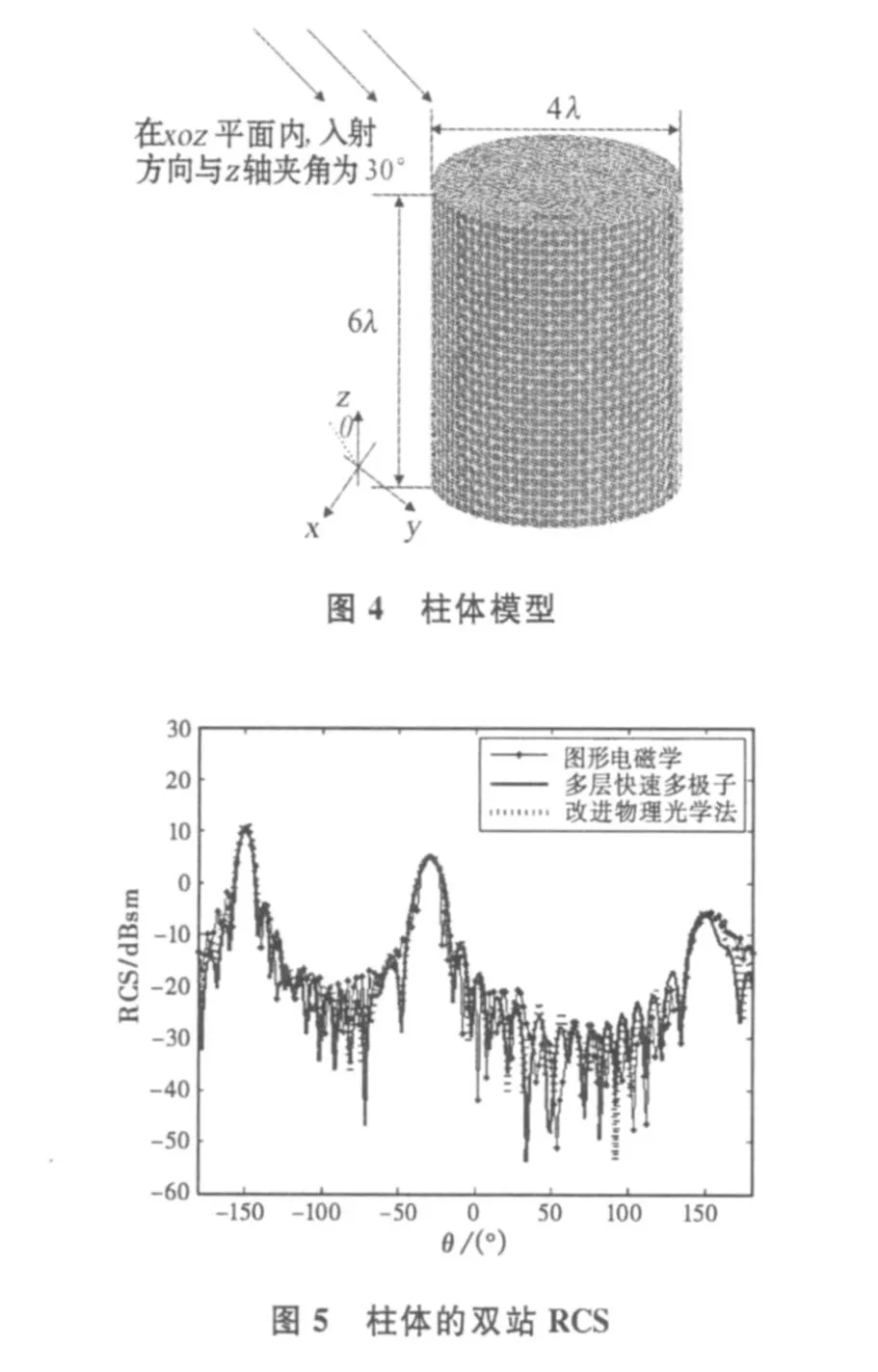
本文利用图形电磁学计算光照区的表面电流,提取电流步进法中的耦合项散射场对传统物理光学算法进行修正。众所周知,作为一种高效的数值计算方法,多层快速多极子方法具有良好的精度。为了验证改进物理光学法的有效性和准确性,下面以电大柱体为例,并与多层快速多极子以及传统的图形电磁学方法进行对比。如图4所示,柱体的半径为2λ,柱体的长度为6λ,入射波频率为 10 GHz。在xoz平面内,入射方向与z轴夹角为30°,极化方式为垂直极化,双站散射方向设为在xoz平面内环绕原点旋转一周。表1给出了各方法所用内存与计算时间,图5给出了各方法的计算结果。

表1 各方法所用内存与计算时间
从图5中可以看出,改进物理光学法能够准确地得到表面电流产生的散射场,与多层快速多极子方法的计算结果吻合较好。
如图6所示,现选取复杂圆台与圆柱组合体作为比较分析的计算模型,圆台的上底面半径为λ,高为2 λ,圆柱体的半径为2λ,柱体的长度10λ,入射波频率为10 GHz,垂直极化。在xoz平面,入射波方向与z轴夹角为30°,将计算结果与PO-MOM 的混合方法以及传统的图形电磁学结果进行比较验证,结果如图7。表2给出了各方法所用内存与计算时间。

图6 圆台与圆柱组合体模型
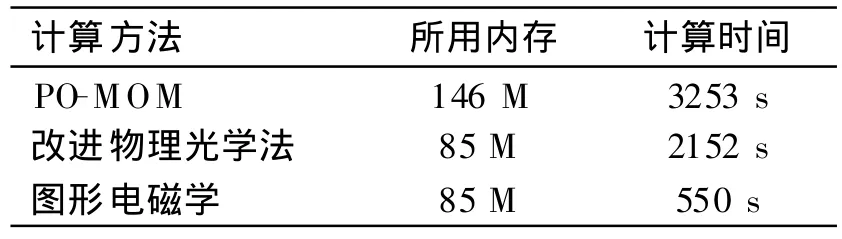
表2 各方法所用内存与计算时间
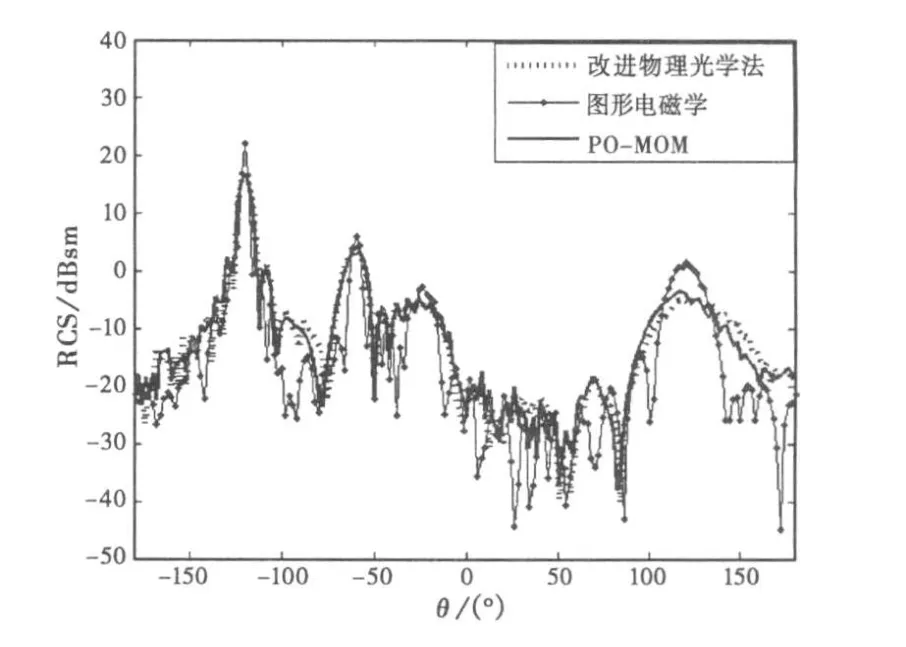
图7 圆台与圆柱组合体的双站RCS
从图7可以看到,仅仅利用传统图形电磁学考虑电大导体目标的电磁散射,结果还是存在一定误差的。将电流步进法引入阴影面表面电流计算中,与图形电磁学方法相结合,可以更为准确地计算电大复杂导体目标的 RCS,数值计算结果与POMOM方法的结果较好地吻合,在精度方面能够满足RCS计算要求,在时间上面具有一定的优势。综合以上两个计算实例可以说明:改进物理光学法比传统的图形电磁学法的计算准确性有极大提高,而所用计算机存储量比数值计算方法大大减小,计算时间也在很大程度上减少。随着电尺寸的增大,多层快速多极子方法所需存储量和计算量迅速增大。在计算简单电大加复杂电小尺寸目标单站RCS时,PO-MOM方法比较有效,但是处理双站问题需要考虑电大尺寸的阴影面,仍然会存在内存和时间的限制。尽管传统的图形电磁学法计算时间很短,但它较大的计算误差常常令其难以满足精度要求。相比之下,改进物理光学法结合高频算法的优点,既能有效避免对整体目标花费大量的内存和时间进行求解,又可以较好地满足计算精度要求。
4.结 论
本文研究了电大目标双站电磁散射的改进物理光学法。针对以往双站高频算法由于忽略阴影区电流影响,导致大双站角下计算误差有所增大的问题,提取电流步进法中的迭代算子,考虑阴影区不同面元的耦合影响,对阴影面电流进行准确计算,并与图形电磁计算方法相结合,推导出了修正的物理光学公式。对照明区采用物理光学近似进行求解;对阴影区面元,按照入射波方向进行排序迭代求解,从而能够在考虑阴影面电流影响的基础上,快速有效地计算复杂目标的双站RCS。
[1] 阮颖铮.雷达截面与隐身技术[M〛.北京:国防工业出版,1998:5-10.
[2] YEE K S.Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J].IEEE Trans.Antennas Propag,1966,14(3):302-307.
[3] ZAPOROZHETS A A,LEVY M F.Current marching technique for electromagnetic scattering computations[J].IEEE Trans.Antennas Propag,1999,47(6):1016-1024.
[4] ZAPOROZHETS A A,LEVY M F.Bistatic RCScalculations with the vector parabolic equation method[J].IEEE Trans.Antennas Propag,1999,47(11):1688-1696.
[5] DJORDJEVIC M,NOTARO B M.Higher order hybrid method of moments–physical optics modeling technique for radiation and scattering f rom large perfectly conducting surfaces[J].IEEE Trans.Antennas Propag,2005,53(2):800-813.
[6] QIN Dehua,WANG Baofa.Bistatic RCS prediction with graphical electromagnetic computing(GRECO)method for moving targets[J].Chinese Journal of Aeronautics,2002,15(3):161-165.
[7] 李建周,毛继志,许家栋.一体化双站散射图形算法[J].微波学报.2004,20(1):19-22.LI Jianzhou,MAO Jizhi,XU Jiadong.Integrative graphical electromagnetic computation for bistatic scattering[J].Journal of microwaves,2004,20(1):19-22.(in Chinese)
[8] CATEDRA F,DELGADO C,DIEGO I G.New physical optics approach for an efficient treatment of multiple bounces in curved bodies defined by an impedance boundary condition[J].IEEE Trans.Antennas Propag,2008,56(3):728-736.
[9] 黄沛霖,姬金祖,武哲.飞行器目标的双站散射特性研究[J].西安电子科技大学学报.2008,35(1):140-143.HUANG Peilin,JI Jinzu,WU Zhe.Research on the bistatic RCS characteristic of aircraft[J].Journal of Xidian University,2008,35(1):140-143.(in Chinese)
[10] RIUS J M,FERRANDO M,JOGRE L.High-Frequency RCSof complex radar targets in real-time[J].IEEE Trans.Antennas Propag,1993,41(9):1308-1460.
[11] LI Xiaofeng,XIE Yongjun,YANG Rui.High-frequency method for scattering from coated targets with electrically large size in half space[J].IET Microw.Antennas Propag,2009(l3):181-186.
[12] YOUSSEF N N.Radar cross section of complex targets[J].IEEE Proc,1989,77(5):722-734.

