高纬极区D、E层等离子体非相干散射谱研究
姬红兵 王 玮 李 林
(西安电子科技大学电子工程学院,陕西西安710071)
1.引 言
非相干散射雷达利用高空大气中等离子体热起伏的微弱信号来遥测高空大气的物理参数,能够对多种电离层等离子体的重要参数同时进行测量,而且测量区域可覆盖D区到两千公里左右的高度范围,已成为目前研究电离层结构与动力学过程的最强有力的地面探测工具。但是目前的非相干雷达实验处理数据仍是基于最基本的麦克斯韦分布理论,然而高纬极区出现的大规模对流电场和高能粒子的沉降,以及人工加热电离层等,都会导致等离子体分布函数偏离麦克斯韦分布。因此,早在上世纪80年代初期,Raman[1]等人就将非麦克斯韦函数分布的研究应用于极光区电离层散射谱的计算,首先给出了任意视线方向离子速度分布函数。国内的郑传青、吴健[2-3]等人对双麦克斯韦分布函数进行了修正,给出了速度函数的解析解形式。Suvanto[4]采用了一个巧妙的方法处理了柯西主值积分,从而对非相干散射谱进行了模拟。St-Maurice和Schunk[5-7]对多种碰撞模式下的速度分布函数进行了讨论,给出了弛豫碰撞下的积分解,以麦克斯韦,双麦克斯韦和环形麦克斯韦分布为权函数,给出了极化碰撞和共振电荷交换碰撞下的正交多项式解。徐彬、薛昆和吴健[8-11]等根据Grad[12]理论,将离子速度分布函数展开成正交级数的形式,讨论了以麦克斯韦分布为权函数展开的13矩近似和20矩近似的功率谱特征以及以双麦克斯韦分布为权函数展开的16矩近似的功率谱特征。在人工加热电离层方面,Satio[13]等最近又认为电子速度分布函数为kappa分布,而将离子速度分布函数看成是麦克斯韦分布。
由于徐彬和薛昆等在13矩近似下和16矩近似下的功率谱研究中,仅对速度分布函数引入碰撞,在功率谱计算中并没有考虑碰撞等因素[8,11],其理论仅适用于高纬极区F层的实际情况。在电离层的D、E层中,由于电离程度较弱,电子和离子与中性成分的碰撞较为剧烈,在研究高纬极区中低高度电离层等离子体的散射谱时,需要考虑碰撞的影响。本文根据Sheffield[14]碰撞等离子体非相干散射谱理论,采用离子13矩和16矩近似速度分布函数对碰撞等离子体散射谱进行模拟。计算了不同碰撞频率、不同电场、不同碰撞频率与回旋频率比值条件下的功率谱。一方面,通过与不考虑碰撞的结果进行对比,发现考虑碰撞的散射谱在碰撞频率增大时,波峰幅值和峰谷比均明显增大,谱向中心方向聚拢,波形变得愈加尖锐,且功率谱越趋于麦克斯韦分布,这一变化就越为明显。另一方面,将16矩近似的功率谱与13矩近似的功率谱进行对比,发现随着电场强度的增强,离子温度各向异性特征加剧,两者的功率谱差异随之增大。与13矩近似相比,16矩近似能够更加准确地描述以碰撞剧烈且温度各向异性显著为特征的高纬极区中低层等离子体。
2.离子速度分布函数
2.1 13矩近似
由于在高纬极区的电离层中,存在大的对流电场,因此,离子的速度分布函数严重偏离麦克斯韦分布,基于Grad理论的离子13矩近似分布可以较好地描述温度各向异性特征不明显的等离子体离子非麦克斯韦速度分布。
离子的速度分布函数通过玻耳兹曼方程得到,在弛豫碰撞模型下,假设等离子体是空间均匀并处于稳态,则此时玻耳兹曼方程可以表示为
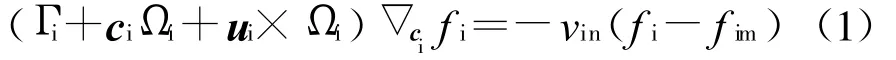
式中:Γi=ei E/mi,Ωi=ei B/mic,E和B都是环境场而忽略等离子体的自洽场,c是光速,ei是离子的带电量。简单起见,定义随机速度ci=v-ui,其中u i是离子的漂移速度,则根据Grad理论,离子分布函数为
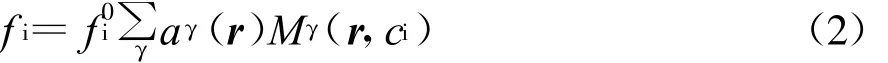
式中:Mγ是一系列完整的正交多项式;aγ是展开系数是麦克斯韦分布函数。
Grad理论以麦克斯韦函数为基展开,13矩近似中包括了粘滞项和热流矢量项的贡献,它可以用下式进行表示[15]

为了得到任意视线方向的分布函数,采用pqr坐标系来分析和讨论离子分布函数。XYZ和pqr坐标系的变换关系,如图1所示。

由此,可以得到任意视线方向上离子13矩近似下的速度分布函数为
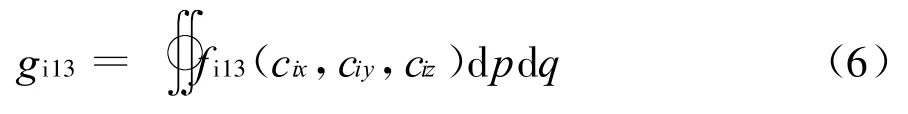
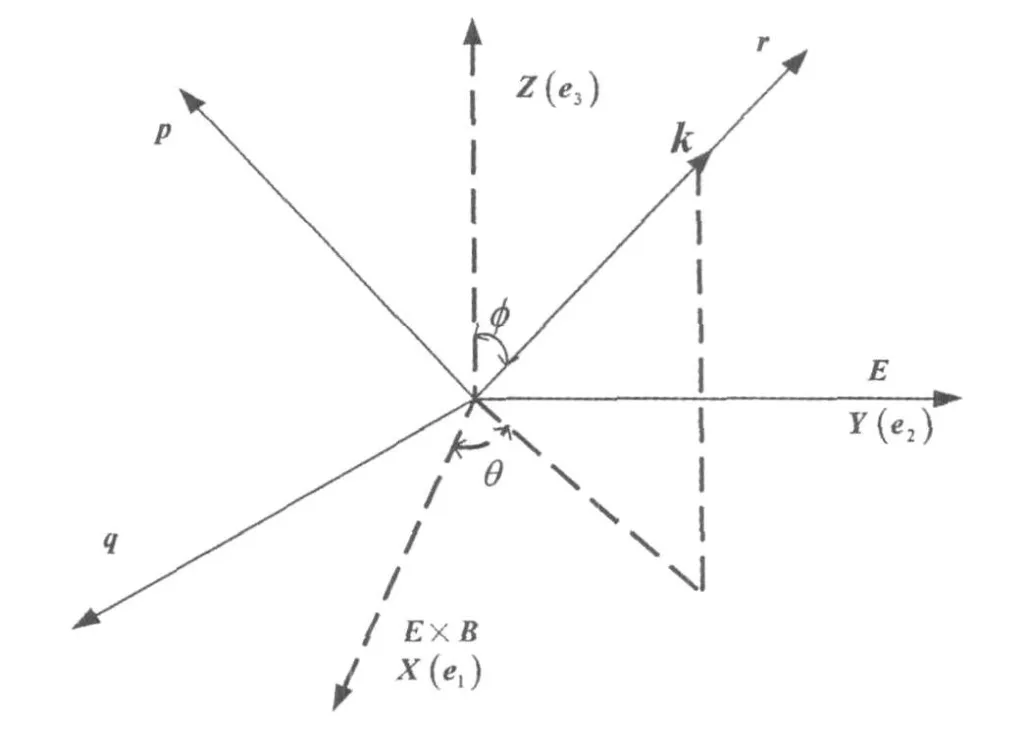
图1 XYZ坐标系和pqr坐标系的变换关系
2.2 16矩近似
由于13矩近似的权函数为麦克斯韦分布,使得该分布不适于描述温度各项异性特征显著的等离子体。此时,可以用基于双麦克斯韦分布函数展开的16矩近似来描述[15]。与13矩近似类似,16矩近似同样包含有热流矢量项和粘滞项的贡献,它可以表示为


式中,为双麦克斯韦分布函数分别为平行于磁场方向和垂直于磁场方向的离子温度,视线方向的离子温度需要使用有效温度Tif替换

将式(5)代入式(7),并对垂直于视线方向的两个坐标轴进行积分,可得到任意视线方向上离子16矩近似下的速度分布函数为
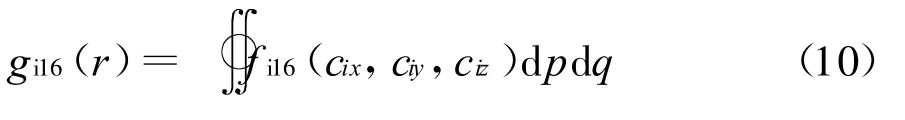
3.考虑碰撞的等离子体非相干散射谱
由于高纬极区电离层的D、E层电离程度较弱,电子和离子与中性成分的碰撞较为剧烈,为使理论分析的结果更加贴近实际,需要考虑碰撞的影响。
根据Sheffield的理论,任意速度分布下碰撞等离子体的非相干散射谱为
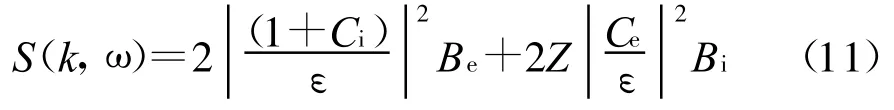
式中:k为波数;Z为离子电荷数;ε=1+Ci+Ce为径向介电常数;Ci和Ce分别为离子和电子的极化率;Bi和Be为考虑碰撞条件下,单个离子和电子引起的密度波动的功率谱,对于后向散射,其表达式分别为

式中:下标q表示离子或电子;e为电子电量;ne0和ni0为电子和离子密度;fi0和fe0为视线方向上离子和电子的速度分布函数;v为视线方向上的粒子速度;υq为粒子的有效碰撞频率。
求解功率谱的关键在于两种带有复奇点的积分运算
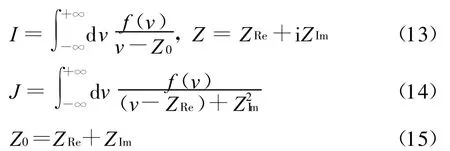
文献[16]中详细推导并给出了以上两种带有复奇点的积分运算结果

式中,∫表示柯西主值积分。
根据式(12)-式(17),这里不考虑人工加热电离层等非自然情况,假定电子服从麦克斯韦分布,即fe0=exp(-v2/a2)/a,则对于电子有
对于离子速度服从13矩近似分布,将式(6)代入式(12)可得

类似地,对于离子速度服从16矩近似分布,将式(10)代入式(12)可得
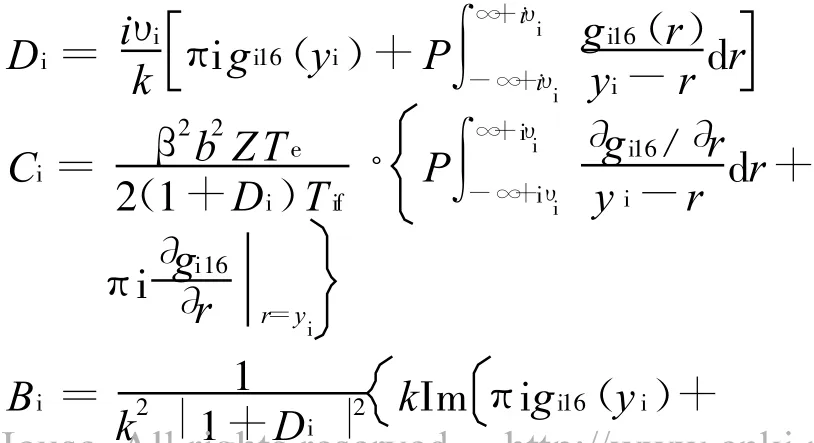
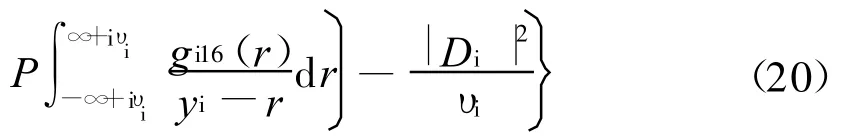
将式(18)、式(19)代入式(11),可得到13矩近似下的碰撞等离子体功率谱;类似地,将式(18)、式(20)代入式(11),即可得到16矩近似下的碰撞等离子体功率谱。
4.仿真实验与分析
假设高纬极区D、E层电离层中的主要成分是NO+离子,中性成分温度为1000 K,电子温度与离子温度比为1.5,电子和离子与中性成分的有效碰撞频率相等,αi表示碰撞频率和回旋频率之比。图2和图3给出了电场强度为E=40 mV/m时,根据Shffield不考虑碰撞的等离子体理论分别得到的16矩近似和13矩近似下的等离子体散射谱。

图4、图5分别给出了电场强度为E=40 mV/m,碰撞频率为8000 Hz时,16矩近似和13矩近似下等离子体功率谱随αi变化的结果。
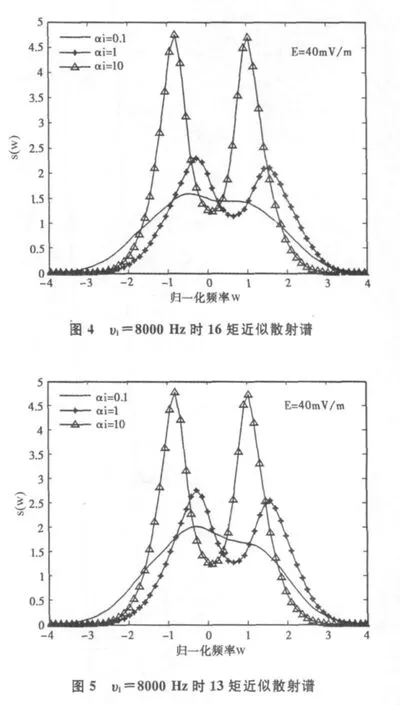
图6、图7分别给出了碰撞频率为5000 Hz,αi=1时,16矩近似和13矩近似的功率谱随电场强度变化的结果。
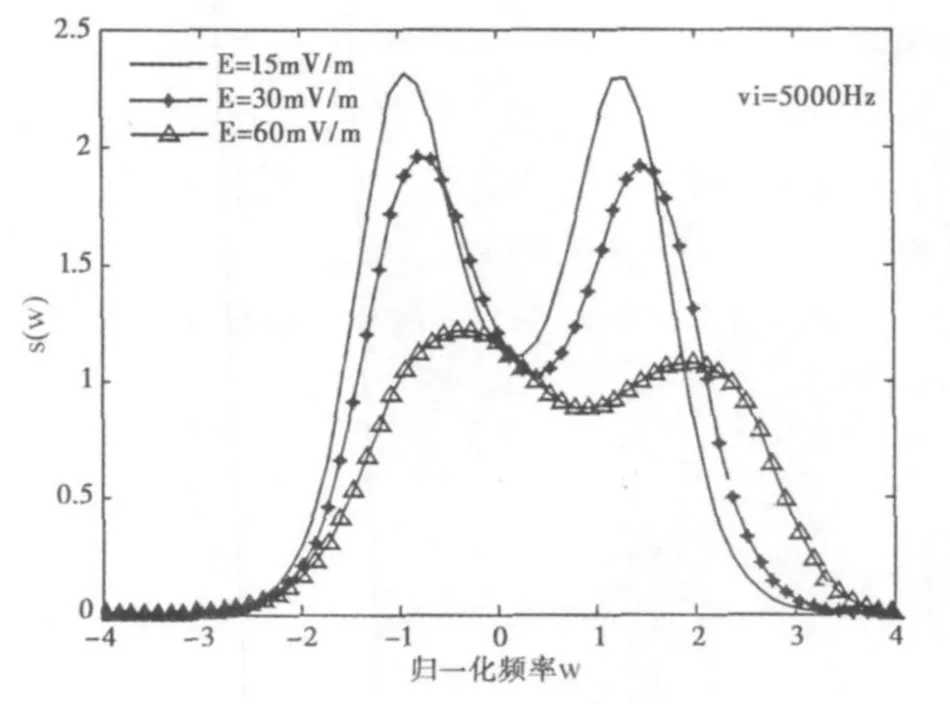
图6 不同电场强度下16矩近似散射谱
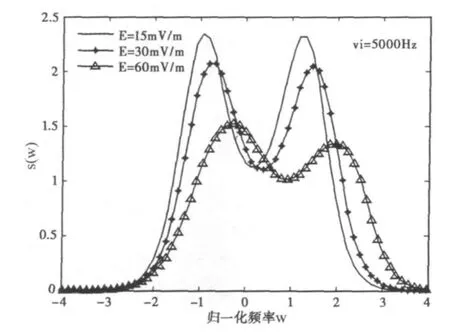
图7 不同电场强度下13矩近似散射谱
由图2、图3可以看出,不考虑碰撞的情况下,当αi较小时,功率谱发生漂移并且不对称现象明显,随着αi的增大,功率谱逐渐趋于麦克斯韦分布。
由图4、图5可以看出,当碰撞频率为8000 Hz时,碰撞频率对功率谱有着显著的直接影响,不同αi下的波峰幅值均有所增大,谱向中心聚拢,随着αi的增大,功率谱逐渐趋于麦克斯韦分布。当αi=10时,功率谱峰值最大,波形最尖锐,而当 αi分别为 1和0.1时,功率谱由于显著偏离麦克斯韦分布,波形相对平缓很多。可以看出:功率谱越靠近麦克斯韦分布,碰撞频率的直接影响就越大。
由图6、图7可以看出,当碰撞频率为5000 Hz时,随着电场强度的增强,两种离子速度功率谱均发生不对称漂移现象,电场越强,离子温度各向异性越明显,两者的功率谱差异就越大。这与徐彬、薛昆等[9]在不考虑碰撞条件下所给出的结论是一致的。
综上所述,通过对碰撞等离子体功率谱与不考虑碰撞的等离子体功率谱进行对比,发现在不考虑碰撞的功率谱计算中,最终是离子的碰撞频率与离子的回旋频率之比影响了离子的速度分布函数,从而又间接影响了功率谱。而在碰撞等离子体的功率谱计算中,不仅存在该比值的间接影响,粒子的有效碰撞频率也直接作用于功率谱。因此,一方面在弛豫模型下,随着离子碰撞频率与离子回旋频率比值的增大,功率谱愈加趋于麦克斯韦分布;另一方面,碰撞项的直接作用又使得谱峰增大,谱形变得尖锐,且谱宽变窄,谱向中心聚拢。
通过对13矩近似与16矩近似下不同电场强度的碰撞等离子体功率谱进行对比,可以得到与不考虑碰撞的情况相似的结论:由于16矩近似下,垂直于磁场方向的离子温度与电场强度成正比,温度各向异性的程度随着对流电场强度的增加而增大,两者的功率谱差异也随之增大。考虑到高纬极区中低高度的电离层中存在大规模对流电场,温度各向异性特征显著且碰撞剧烈。因此,基于双麦克斯韦分布展开的16矩近似可以得到比13矩近似更加接近实际的谱估计结果。
5.结 论
本文给出了离子13矩和16矩近似下碰撞等离子体的功率谱,与先前的文章相比,更加符合高纬极区D、E层的实际情况。此外,研究发现与13矩相比,16矩近似能够更加准确地描述以碰撞剧烈且温度各向异性显著为特征的高纬极区中低层等离子体。由于13矩近似和16矩近似都只考虑了粘滞项与热流矢量项的影响,且没有考虑平行电场,因此,为了能更好地估计实际的功率谱,需要提出更为合理的非麦克斯韦速度分布。
[1] VENKAT RAMAN R S,St-MAURICE JP,ONG R S B.Incoherent scattering of radar waves in the auroral ionosphere[J].Journal of Geophysical Research,1981,86(A 6):4751-4762.
[2] 吴 健.极光区离子分布函数视线方向上的解析解及其饱和现象[J].地球物理学报,1997,40(6):739-746.WU Jian.An analytical form of the raman et al.ion velocity distribution in auroral ionospheric F-region and the distribution saturation with increase of electric field[J].Chinese Journal of Geophysics,1997,40(6):739-746.(in Chinese)
[3] 郑传青,吴 健.高纬电离层中非麦克斯韦分布等离子体的非相干散射谱的模拟[J].地球物理学报,1994,37(4):433-439.ZHENG Chuanqing,WU Jian.Spectra of non-maxwellian plasma in the high-latitude ionosphere[J].Chinese Journal of Geophysics,1994,37(4):433-439.(in Chinese)
[4] SUVANTO K.Non-Maxwellian Ion Velocity Distributions in the Ionospheric F-Region[C].EISCAT technical note,1989.
[5] St-MAURICE J P,SCHUNK R W.Auroral ion velocity distributions using a relaxation model[J].Planet Space Sci,1973,21(7):1115-1130.
[6] St-MAURICE J P,SCHUNK R W.Use of Generalized Orthogonal Ppolynomial Solutions of Boltzmann's Equation in Certain Aeronomy Problems:Auroral Ion Velocity Distribution[J].J Geophy Res,1976,81(13):2145-2154.
[7] St-Maurice J P,Schunk R W.Auroral Ion Velocity Distributions for a Polarization Collision Model[J].Planet Space Sci,1977,25(3):243-260.
[8] 徐 彬,薛 昆,吴 健,等.具有13阶矩近似分布函数的等离子体的非相干散射谱[J].中国科学,2008,38(1):103-110.XU Bin,XUE Kun,WU Jian,et al.Incoherent Spectra of Plasma with 13-Moment Approximation for Velocity Distributions[J].Sciencein China Press,2008,38(1):103-110.(in Chinese)
[9] 薛 昆,徐 彬,吴 健,等.弛豫碰撞模型下非相干散射谱的计算[J].自然科学进展,2007,17(11):1565-1571.XUEKun,XU Bin,WU Jian,et al.The Computation of Incoherent Spectra in Relax Collision Model[J].Progress in Natural Science,2007,17(11):1565-1571.(in Chinese)
[10] 薛 昆,郭立新,吴 健,等.离子分布函数的20阶矩近似在非相干散射谱中的应用[J].地球物理学报,2009,52(4):878-886.XUE Kun,GUO Lixin,WU Jian,et al.Application of 20-Moment Approximation for Ion Velocity Distribution Function in Calculations of Incoherent Scatter Spectra[J].Chinese Journal of Geophysics,2009,52(4):878-886.(in Chinese)
[11] 薛 昆.高纬极区电离层非相干散射谱的理论和实验研究[D].西安:西安电子科技大学,2009.XUE Kun.Theoretical and Experiment Study on the Incoherent Scatter Spectra of High Latitude Auroral Ionosphere[D].Xi'an:Xidian Univesity,2009.
[12] GRAD H.Principles of the Kinetic Theory of Gases[M].Berlin:Springer Verlag,1958,205-294.
[13] SAITO S,FORME F R E,BUCHERT S C,et al.Effects of a kappa distribution function of electrons on incoherent scatter spectra[J].Ann.Geophysicae,2000,18:1216-1233.
[14] SHEFFIELD J.Plasma Scattering of Electromagnetic Radiation[M].New York:Academic Press,1975,113-128.
[15] St-MAURICE J P,SCHUNK R W.Ion velocity distribution in the high-latitude ionosphere[J].Reviews of Geophysics and Space Physics,1979,17(1):99-133.
[16] 徐 彬,吴振森,吴 健,等.碰撞等离子体的非相干散射谱[J].物理学报,2009,58(7):5104-5110.XU Bin,WU Zhensen,WU Jian,et al.Incoherent scatter spectrum of a collision plasma[J].Journal of Physics,2009,58(7):5104-5110.(in Chinese)
[17] 徐 彬,吴振森,吴 健,等.电离层加热期间非相干散射的反演[J].电波科学学报,2008,23(4):713-716.XU Bin,WU Zhensen,WU Jian,et al.Inversion of incoherent scatter spectra during ionosphere heationg[J].Chinese Journal of Radio Science,2008,23(4):713-716.(in Chinese)
[18] 吴永宏,吴 健,吴振森.非相干散射的一种非线性反演算法[J].电波科学学报,2008,23(1):74-78.WU Yonghong,WU Jian,WU Zhensen.Non-linear inversion algorithm for incoherent scattering[J].Chinese Journal of Radio Science,2008,23(1):74-78.(in Chinese)

