基于Excel的 水力学隐式方程求解与辅助绘图
鲍新华,卢文喜,李鸿雁,才文韬,谭剑锋
(吉林大学环境与资源学院,吉林 长春 130026)
在管路水力计算、明渠临界水深与均匀流水深计算、河道水面曲线计算、水跃共扼水深与水力消能计算、堰流计算以及某些经验公式(如沿程阻力系数)等水力计算中,经常遇到求解隐式方程问题。试算法(含辅助图解法)、标准曲线图解法是常用的一类传统方法[1~3]。这些传统方法虽有优点,但不足也是明显的。如试算法虽可以充分发挥计算者的经验判断,有时能给出比较接近结果的初值并较快得到结果,但由于求解常需要反复试算,有时配合辅助图解法还存在读数的精度误差。
Excel作为Office常用组件之一,在工程与管理行业的统计、计算方面得到了全面的应用,但在水力计算中用于求解隐式方程还不多见[4,5]。由于Excel的数据运算能力、图表功能和内含的单变量求解功能,将其引入水力学中求解隐式方程,与传统方法相比具有求解简单方便,通用性强的特点。
选用几个水力学隐式方程典型算例,应用Excel单变量求解、迭代求解和辅助做图功能,说明Excel用于水力学计算的简单与方便。
1 Excel单变量求解
1.1 均匀流水深h或底宽b求解
例1:数据选自文献[1]例5.3。已知等腰梯形断面渠道设计流量Q,底坡i,底宽b,边坡系数m和粗糙系数n,求均匀流水深h0。
从明渠均匀流基本公式入手,谢才系数采用曼宁公式,可以给出这种情况下的流量公式:

Excel单变量求解这一隐式方程基本过程为:在Excel工作表中A1∶F1单元格中输入变量符号(仅作为标识,不参与运算),A2单元格中输入上面的公式(注意公式以等号开始),B2∶E2输入相应已知数值。当光标在任意单元格时,从“工具—单变量求解”出现的对话框中选择输入“目标单元格”和“可变单元格”绝对地址,然后输入流量Q的目标值70后,见图1。按确定则有求解结果为(图 2)

图1 单变量求解均匀流水深过程
结果与文献[1]基本相同,但由于试算法的近似和辅助做图读数的误差,Excel单变量求解的精度显然要高些。

图2 单变量求解均匀流水深结果
1.2 非均匀流临界水深hk求解
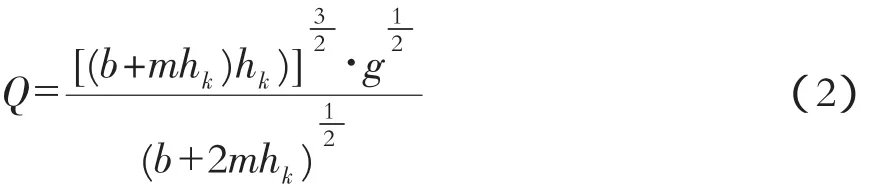
例2:数据选自文献[1]例6.3。采用上面类似的方法,Excel单变量求解上述隐式方程的临界水深 hk为 2.25 m(见图 3)。

图3 单变量求解等腰梯形断面临界水深hk
需要说明的是,求解前上述C2∶E2单元格的公式是按照公式(2)输入的。
从上面2例可以看出,与试算法(含辅助图解法)和标准曲线图解法相比,Excel单变量求解水力学隐式方程,可体现出2个优点:①求解过程简单,结果精度高。由于试算法需要多次反复试算,求解工作量较大。在不能大量试算的情况下,结果精度必然要受影响。试算的辅助图解法和标准曲线(需有标准曲线模板)图解,则有读数误差的影响。②对同一隐式方程,Excel单变量求解的工作表可以作为模板使用。参数不同,求解过程相同。由于隐式方程(如公式(1)或(2))是不变的,因此稍显麻烦的公式仅需输入一次,保留后就可以作为模板下次使用,使用时仅需要改变另一同类问题参数的数值再求解就可以了。特别是对同一隐式方程不同求解问题,只要使用的隐式方程不变,求解过程也是不变的。如在公式(1)中,在均匀流水深h和其它参数已知时求解底宽b,需要变化的只是可变单元格由h对应格变为b对应格而已(如例1中,可变单元格由F2变为B2),而这点变化对于求解并不增加任何工作量。
2 Excel迭代法求解
迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,也是隐式方程的另一种解法。这里我们主要采用简单迭代法[6]。简单迭代法在教材中均有少量介绍[1~3],由于求解多采用计数器或编程法进行,一定程度上限制了迭代法的应用。而将Excel工具引入水力学隐式方程迭代求解具有简单方便的特点。
水力学隐式方程采用迭代解法,首先应该根据隐式方程或方程的变形来确定迭代关系。隐式方程适当的变形可以有效减少迭代次数。其次是迭代初值的选择,好的初值依靠经验,不适当的初值可能导致不收敛情况的出现。再次是确定迭代结束的条件,通常可以迭代相对误差来控制。考虑到初值常以0值开始和一次迭代有时就可能满足精度要求的特例,取δ=更不失一般性。当迭代相对误差很小时,比如小于1%,则可以结束迭代。
2.1 均匀流水深h或底宽b求解
例3:仍以上面例1数据为例,迭代求解等腰梯形均匀流水深h0。
对公式(1)变形有:

采用Excel进行迭代计算如下:
打开Excel表,输入表头标识,即将已知参数Qi,b,m,n,h0i,h0i+1,相对误差 δ输入到单元格内,然后把已知参数值输入到下一行相应位置。在G2单元格(h0i+1单元格)内输入下列公式(即公式(3),注意单元格地址的绝对和相对引用)=($E$2*$A$2/($B$2^(1/2)))^(3/5)*(($C$2+2*F2*((1+$D$2*$D$2)^(1/2)))^(2/5))/($C$2+$D$2*F2)
取h0i=0为初值,在F2单元格内输入初值0,在F3单元格内输入=G2,,在H2单元格内输入=ABS(G2-F2)/G2⋆100,然后拖动填充柄对单元格G3和H2分别向下复制公式,公式复制的过程实际上就是Excel的迭代过程!迭代终止以相对误差小于1%作为结束标志,最终结果取满足要求时h0i+1单元格中的数值。从图4可以看出,本例仅迭代2次就达到了给定的精度要求,结果与前面单变量求解结果是一致的(见图2,4)。

图4 迭代法求解均匀流水深结果
在例1中,如果已知等腰梯形断面渠道设计流量Q,底坡i,均匀流水深h0,边坡系数m和粗糙系数n,求底宽b。则可以对式(3)变形有:

迭代求解方法与例3类似,此略。
2.2 沿程阻力系数λ求解
例4:例题取自文献[3],已知雷诺数Re=48 595,水流型态处于紊流光滑区,要求采用尼古拉兹光滑管公式计算沿程阻力系数λ。
尼古拉兹光滑管公式变形为迭代形式为
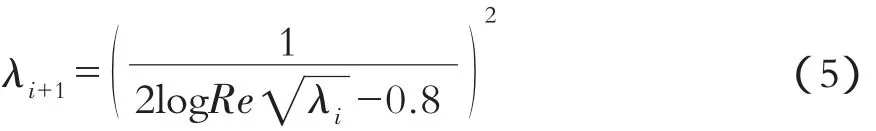
Excel迭代运算表见图5。取不同非零初值(对数函数自变量不能取零值),不同迭代初值对应结果见表1。

图5 迭代法求解沿程阻力系数λ
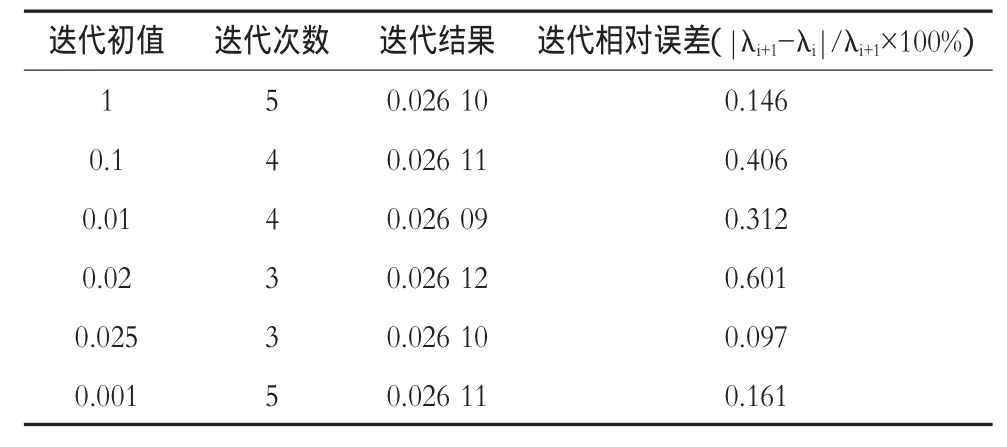
表1 沿程阻力系数λ迭代结果比较
从某种意义上看,水力学隐式方程的迭代解法类似有序的试算法,是从一个初始值出发,不断逼近精确解的过程。求解前一般先把方程变形为x=f(x)的形式(如公式(3~5)),采用 xi+1=f(xi)迭代式,采用简单迭代法来求解。通过笔者教学中对多数水力学隐式方程计算表明,一般简单迭代法多能收敛并得到满足精度的结果。
此外,观察表1,还应注意到迭代相对误差与结果的误差是有所区别的。例4中取λ=0.026 10作为结果精确值的话,表中有二个相同的结果与此一致(不考虑舍入误差),但它们的迭代相对误差是有区别的,而作为最终结果,其误差应该是一致的。但这种迭代相对误差与结果的误差在应用中基本可以忽略。
从上面的例题看,由于Excel强大的表格运算功能,不用编程就可以利用Excel方便完成迭代过程,这表明使用Excel迭代解法求解水力学隐式方程具有简单方便的特点。需要说明的是,除了简单迭代解法外,牛顿迭代等迭代解法也是可以应用的,限于篇幅,这里就不介绍了。
3 Excel求解与绘图
利用Excel不仅可以对隐式方程进行单变量法和迭代法求解,还可以利用Excel强大的图表功能,对相关问题进行辅助制图,下面举例说明这方面的应用。
例5:例题取自文献[1]例6.6,对长直棱柱状明渠,已知底宽b、边坡系数m、粗糙系数n、流量Q、末端水深h,求明渠均匀流水深h0、临界水深hk,并绘制水面曲线。
首先,选用Excel单变量求解法,求解本问题的均匀流水深h0、临界水深hk见图6,并作为进一步分析的初始数据。
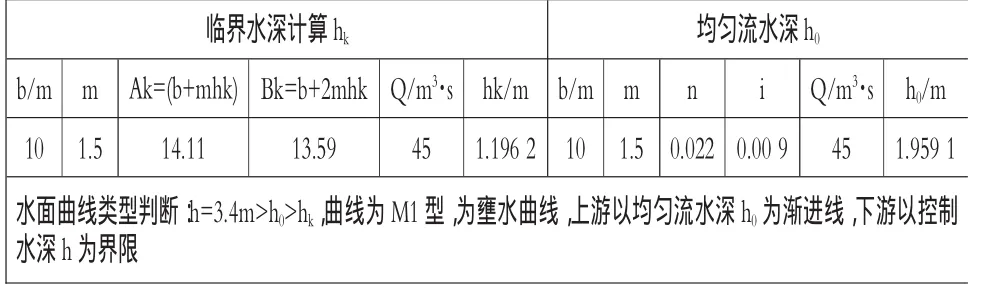
图6 Excel单变量求解均匀流水深h0、临界水深hk
然后利用文献[1]相关公式,用Excel分流段列表计算水深,计算表见图7。
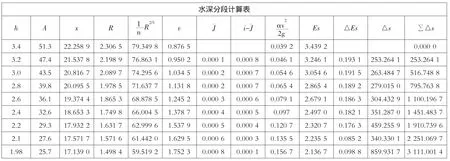
图7 Excel水深分段计算表
为利用Excel绘图,利用图6,7数据,形成一个Excel辅助表(见图8),然后根据辅助表,利用Excel绘图功能绘制的水面曲线见图9。

图8 Excel辅助绘图数据表

图9 Excel绘制的水面曲线
虽然本例中一些具体细节限于篇幅这里没介绍,但对Excel稍有熟悉的读者是不难从上面介绍中掌握这一简单方法的。虽然这里介绍的利用Eecel辅助绘图只是一个简单例子,但由于Excel的基于数据表的强大绘图功能,对水力学中许多数据图,甚至标准曲线等都是可以应用的。
4 结论
从上面几个实例介绍可以看出,Excel的单变量求解法和简单迭代法应用于求解水力学单解隐次方程具有简单方便、精度高和通用性强的特点,可以作为水力学试算法(含辅助图解法)、标准曲线图解法之外的另一种求解方法。将Excel强大的数据处理和绘图功能应用于水力计算中具有简明方便的特点,可以发挥一定的积极作用。
作为已广泛使用的Office办公软件组件之一的Excel工具的使用,在水力计算中,无论是现行教材还是应用文献看,都还不多见。作为一种方便成熟的工具,本文呼吁将Excel应用引入教材,并在实际计算应用中加以积极推广。
[1]吴持恭.水力学[M],第4版.北京:高等教育出版社,2008.
[2]赵振兴,何建京.水力学[M].北京:清华大学出版社,2005.
[3]李大美,杨小亭.水力学[M].武汉:武汉大学出版社,2004.
[4]张 锦.Excel在水力计算中的应用探讨[J].甘肃水利水电技术,2002,38(4):301-302.
[5]邹 健.雍水曲线的新式解法.西部探矿工程[J],2006,8:216-217.
[6]李有法,李晓勤.数值计算方法[M],第2版.北京:高等教育出版社,2005.
[7]Excel规划求解水—岩作用模型[J].地下空间与工程学报,2008,4(2):265-268.

