非线性方程的Excel拟合及在沉降评估中的应用

张志新

（长安大学公路学院，西安710064）

在铁路施工中，为了控制工后沉降，需要进行沉降观测，并将沉降观测的数据，拟合成沉降曲线，用于沉降量的预测和评估。控制工后沉降的技术路线为：沉降观测—曲线拟合—预测—继续观测—曲线拟合—预测—预评估—评估。工后预估条件：（1）沉降时间满足S(t)/S(t=∞)≥75%，式中：S(t)为预测时的沉降观测值；S(t=∞)为预测时的最终沉降值；（2）利用两次回归结果预测的最终沉降差值不应大于8 mm；（3）曲线回归相关系数不应低于0.92。可见，曲线拟合与指标计算是沉降观测的重要环节[1～2，5]。

沉降曲线一般采用两种非线性方程：双曲函数方程和指数函数方程[3～4]。

对于非线性方程的拟合，处理过程比较复杂，一般的工程技术人员难于掌握。目前也有大型的程序可以完成曲线拟合，但费用昂贵，使用也比较复杂，工程应用比较少。

在常用的办公软件Excel中，提供了假设分析命令，该过程通过更改单元格中的值来查看这些更改对工作表中公式结果的影响。规划求解是假设分析的组成部分，通过自动调整所指定的可更改的单元格（可变单元格）中的值，从目标单元格公式中求得结果。利用假设分析命令中的规划求解功能，方便地处理各种复杂非线性方程的拟合[6]。

本文介绍利用Excel进行曲线拟合和预评估指标的计算方法。

1 采用Excel拟合曲线的方法

1.1 基本原理

对于给定拟合曲线方程：S(t)/S∞(1－e-a·t)，式中：S∞—最终沉降量，以开始检测为时间零点；a— 沉降拟合曲线的参数。初步设定参数S∞和a，将t代入方程，计算S(t)，计算S(t)与观测数据的差值，累计差值的平方，反复迭代计算，得出累计平方值最小时的S∞和a，即曲线方程的参数。

1.2 采用Excel拟合曲线的计算步骤

1.2.1 安装规划求解加载宏

用鼠标单击Excel2007左上角office按钮，在弹出的下拉菜单中依次单击“Excel选项”、“加载项”命令，在“管理”栏中选“Excel加载项”，单击“转到”按钮，在“加载宏”对话框中选择“规划求解”，单击“确定”。再次用鼠标单击Excel2007左上角office按钮，在弹出的下拉菜单中依次单击“Excel选项”、“加载项”命令，在“加载项”栏中选定“规划求解加载项”，单击“确定”。点击“数据”菜单后，会出现“规划求解”按钮，如图1。

图1 规划求解加载宏图例

1.2.2 准备数据表

在Excel中建立工作表，设有45组观测数据，时间范围0～336天，见图2。

图2 数据表图例

1.2.3 建立计算模型

在C1栏中增加“沉降值”，在D1栏中增加“离差平方值”，在E1栏中增加“参数”。在C2栏中输入曲线公式“=$E$2*(1-е^(-$E$3*A2))”（以指数函数为例），在D2栏中输入公式“= (C1-B1)^2”，使用自动填充功能填充到最末行；在E4格中输入公式“=SUM(D2:D46)”，在E2、E3中输入参数的初设值，例如10、0.1，如图3。

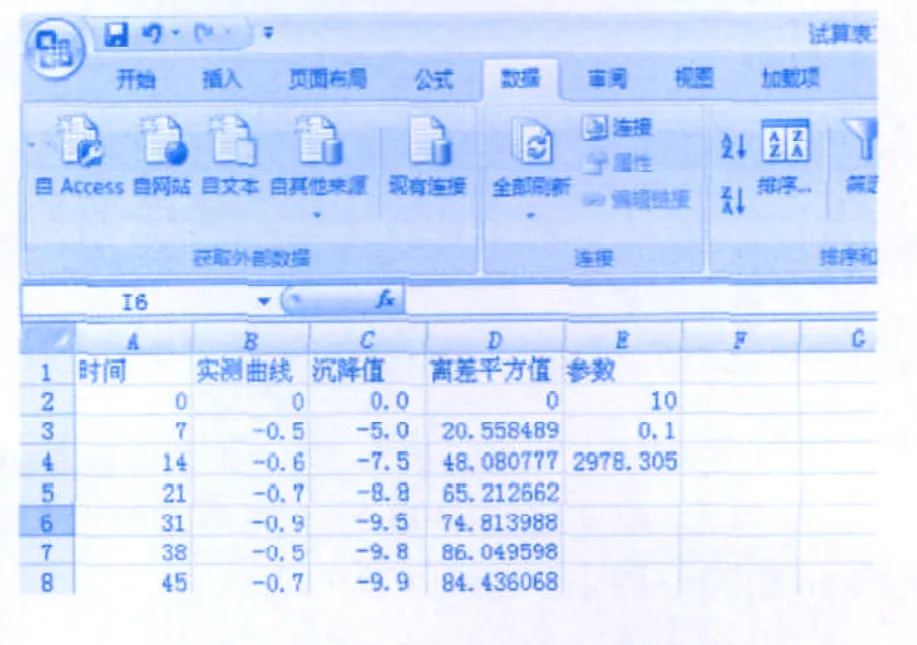
图3 计算模型图例

1.2.4 参数计算

选取“数据”中的“规划求解”出现对话窗，在“设置目标单元格”窗口，输入“$E$4”，选定“最小值”选项，在“可变单元格”窗口中输入“$E$2:$E$3”，如图4。

图4 参数计算图例

在“规划求解参数”和“规划求解选项”对话框中有多个选项，根据“帮助”或专业知识做选择。

单击“求解”，出现“规划求解结果”对话框，如图5。按“确定”，即得出结果，S∞和a分别为E2和E3中的值（2.502 02和0.007 06）。

1.2.5 形成曲线图

框选“时间”、“实测曲线”和“沉降值”3列数据，然后点击“插入”中的“散点图”，选“带直线和数据标记的散点图”，便可形成曲线图。

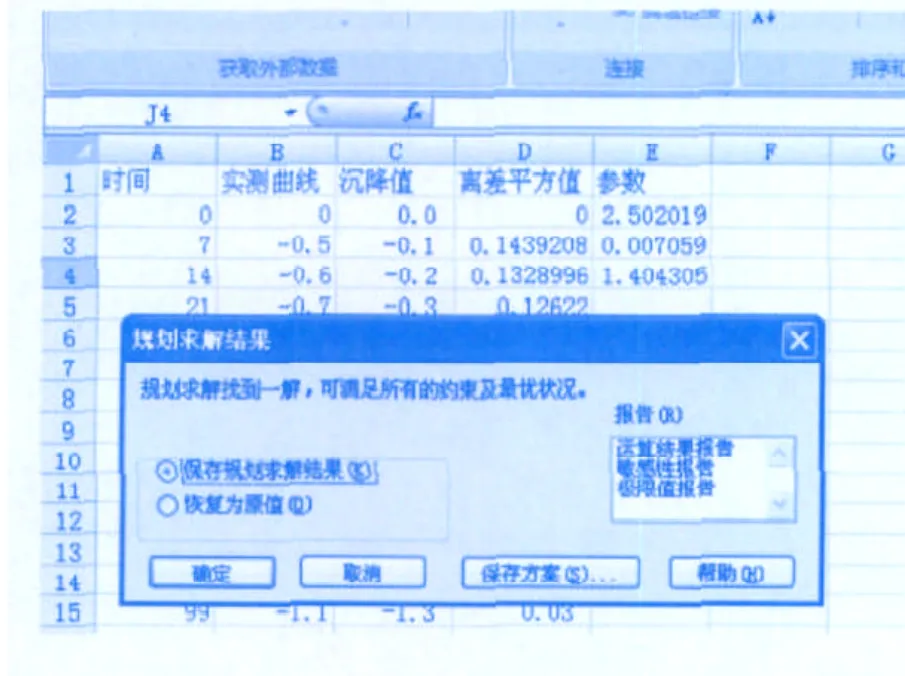
图5 计算结果图例

取3个月（0～243天）前的实测数据，共33组，按照上述方法拟合，得出另一曲线参数S∞和a，分别为2.245 42和0.008 52。将两次拟合的图形显示在同一图上，如图6。

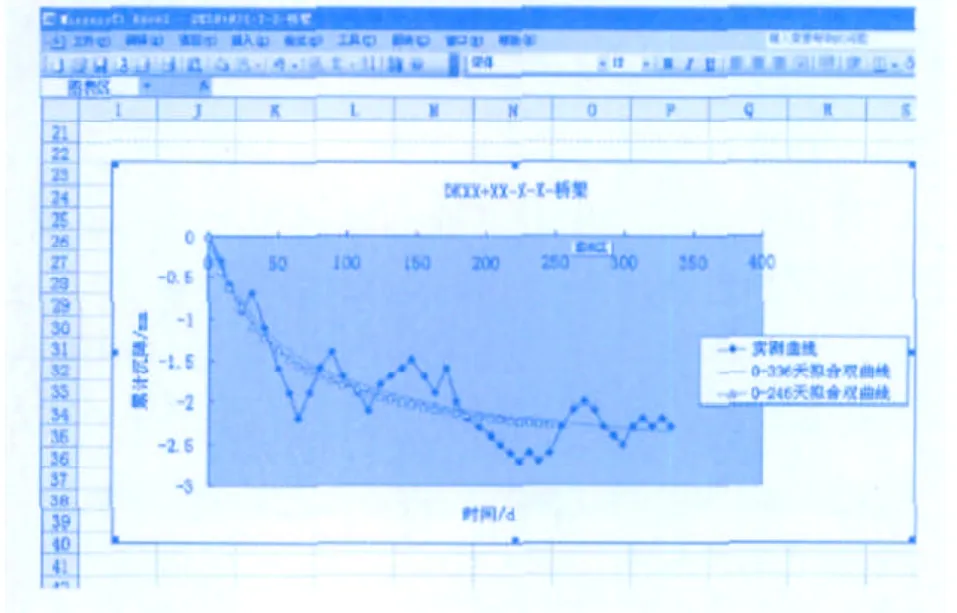
图6 曲线图

2 用Excel进行预估指标的计算

工后预估指标有：（1）S(t)/S(t=∞)，式中：S(t)为预测时的沉降观测值，S(t=∞)为预测时的最终沉降值；（2）利用两次回归结果预测的最终沉降差值；（3）曲线回归相关系数。

在Excel中列表计算，很方便得出上述指标。相关系数的计算公式为其中 x和y是样本平均值 AVERAGE(array1)和 AVERAGE(array2)。利用Excel中的相关系数计算公式计算，语法：CORREL(array1,array2)，其中Array1为第1组数值单元格区域；Array2为第2组数值单元格区域。

计算步骤如下：

（1）在数据栏下方输入表格，如图7。

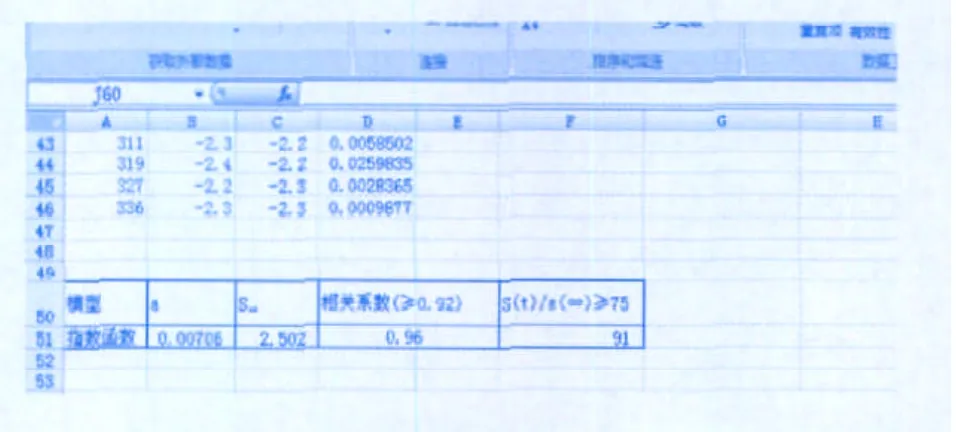
图7 预测指标的计算图例

（2）在B51中输入“=E3”，在C51中输入“=E2”，在D51中输入“=CORREL(B2:B46,C2:C46)”，在F51中输入“=-C46/C51*100”。

（3） 同样，可求得0～243天的实测数据和拟合曲线数值的相关系数以及沉降完成比例值。

（4） 利用两次的S(t=∞)值相减得出两次预测最终沉降差。

3 数据对比检验

为了检验这个方法的正确性和准确性，进行试算。检验数据采用某铁路已经完成沉降评估的数据，采用与检验数据相同的拟合曲线方程和预评估指标。共试算20组数据，试算结果和检验数据中的结果对照如表1。

表1中， S∞即为S(t=∞)。从表1中看出， S∞最大差值为0.43 mm，主要原因是与检验数据所用双曲线模型稍有不同，另外算法上可能稍有不同，因无法分析检验数据所用的程序，故不能做出明确判断。相关系数R差别不大，说明此方法与检验数据所用方法差别不大，最大沉降量差别可以接受。

4 工程应用效果

某段铁路大桥利用Excell处理沉降观测数据，与专用程序结果对比显示，拟合的曲线要素稍有差别，但是预测沉降量差别不大，基本都在2 mm之内。分析原因，是由于拟合算法以及计算精度不同所致。此项差别基本不影响沉降评估结果。

5 结束语

利用Excel中的规划求解功能，分步实现沉降观测中的曲线方程拟合；利用Excel的表格功能，实现沉降预估指标的计算。经过数据检验与实际应用，Excel拟合曲线的方法可以用于沉降评估与预测。用Excel拟合曲线的方法简便易行，但在前后处理方面较差。对于计算偏差和精度，需作进一步研究。

数据检验和实际应用结果证明，本方法和专用程序相比，计算结果有差别，但差别不大。用Excel拟合曲线的方法在前后处理方面仍需要进一步完善。在目前专用程序尚未商业化应用的情况下，本方法可作为沉降观测初步检验分析的手段。

[1] 吴明友. 客运专线无碴轨道铁路工程测量和铺设条件评估关键技术[J] .中国铁路，2006（10）：28-31.

[2] 铁道科学研究院. 客运专线铁路无碴轨道铺设条件评估技术指南[S] . 北京：中国铁道出版社，2006.

[3] 丁愿文. 京津城际铁路桥梁沉降观测与评估技术[J] . 中国工程科学，2009，11（1）：43-47.

[4] 薛保国，武广客运专线桥梁工程沉降观测及数据分析[J] .铁道建筑技术，2009（z1）：9-11.

[5] 客运专线无碴轨道铁路工程测量暂行规定[S] . 北京：中国铁道出版社，2006.

[6] 胡亮，罗康碧，李沪萍. Excel的方程求解功能及其化学化工应用[J] . 昆明理工大学学报（理工版），2002（2）.