任意电流模式滤波器的综合实现
李志军,王春华,刘荣
(1. 湘潭大学 信息工程学院,湖南 湘潭 411105;2. 湖南大学 计算机与通信学院,湖南 长沙 410082)
1 引言
跟电压模式电路相比,电流模式电路因具有宽频带、动态范围大、高频性能好、非线性失真小、工作电压低等优点而成为国内外学术界研究的热点课题[1~15]。电流模式连续时间滤波器已成为一个引人注目的研究方向,并在计算机外围设备和通信电路中得到了广泛地应用[4]。目前对于二阶电流模式滤波器的研究比较成熟,提出了很多典型的电路[5~7]。但对于高阶电流模式滤波器的研究却存在明显的不足。文献[8,9]采用多环反馈法实现了多种结构的任意阶全极点低通滤波器;文献[10,11]采用传递函数直接综合法实现了高阶的巴特沃斯滤波器,该滤波器通过对输入信号的选择可以实现高通、低通、带通等多种滤波功能;文献[12,13]通过对无源 LC梯形网络进行有源模拟实现了高阶切比雪夫低通滤波器和椭圆滤波器,由于该方法必需以固定的LC网络为原型,因而缺乏通用性。在文献[14,15]中,CHANG C M和TU S H采用传递函数分析综合法设计出等电容的电流模式高阶 OTA(operational trans-conductance amplifier)椭圆滤波器结构,但当n为奇数或偶数时必须分别对应不同的滤波器结构。文献[8~15]所设计的高阶滤波器均存在一个共同的缺点:只能实现某一固定类型(巴特沃斯、切比雪夫、椭圆型)的滤波器。本文在上述高阶电流模式滤波器设计方法[8~15]的基础上,以MCCII (multiple outputs current conveyor)为有源器件,采用传递函数分析综合法设计出一种可以实现任意阶(n≥2)、任意类型的电流模式滤波器模型,该模型结构简单,仅由(2n+1)个MCCII器件、n个接地电容和(2n+1)个接地电阻构成。在实现巴特沃斯滤波器时,通过对输出信号进行不同组合可以实现高通、低通、带通、带阻及全通滤波功能。本文给出了三阶椭圆滤波器和六阶巴特沃斯通用滤波器的设计,并分析了器件寄生参数对电路性能的影响,PSPICE仿真结果验证了该模型的正确性。
2 MCCII器件及端口特性
电流传输器(CCII)作为一种新型的电流模式器件,与传统的OA(operational amplifier)相比,具有电源电压低、频率范围宽、动态范围大、线性度好等优点。由于CCII具有电压输入端和电流输入端,因而可以方便地实现电压模式和电流模式信号处理电路。由于在设计中多端输出的电流传输器能更加简化电路,所以一般在 CCII的基础上通过附加电流镜实现多端输出的 MCCII。本设计中采用的MCCII包含3个电流输出端(2个同相电流输出端,一个反相电流输出端),其电路符号及内部电路如图1所示,理想端口特性为[7]

其中,IZ1~IZ2为同相电流输出,为反相电流输出。
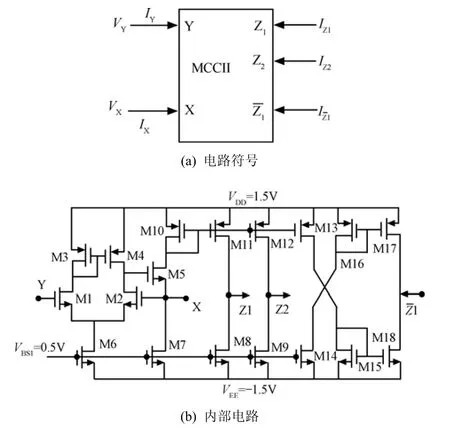
图1 MCCII电路符号及实现电路
3 任意电流模式滤波器的实现
3.1 任意滤波器模型的实现
任意的电流模式滤波器的传输函数可以描述为

引入n+1个内部电流变量,则
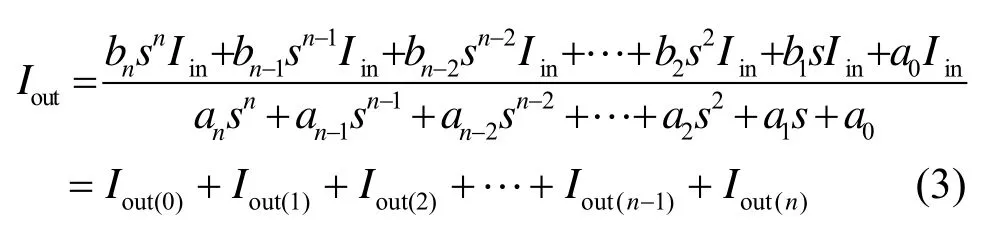
其中
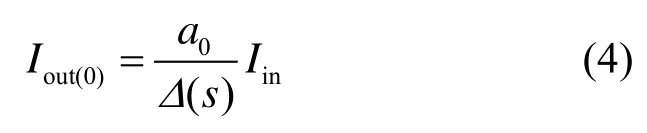

根据式(4)~式(6)可以得到
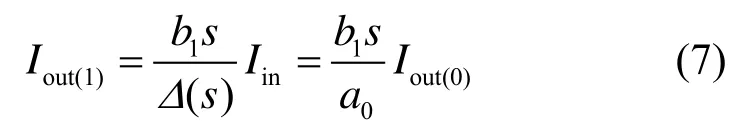

从式(7)~式(10)可以确定式(3)各内部电流之间依次为积分关系。用MCCII实现的电流积分器如图2所示,图中bi为积分电容的大小,bi-1为MCCII器件X端口所接电阻的电导值。根据MCCII的端口特性可以得到图2电流积分器的传递函数

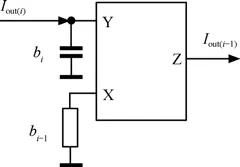
图2 电流积分器的实现电路
将式(4)交叉相乘,得

可以整理为
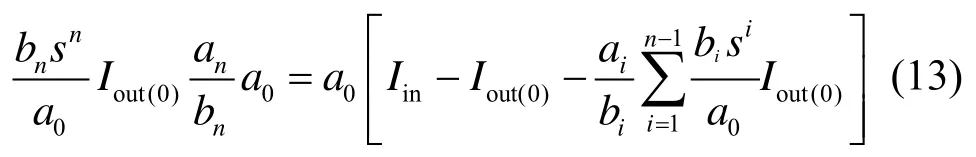
将式(7)~式(10)代入并整理得

由基尔霍夫电流定律可以确定输入电流 Iin与各积分器输出电流之间的关系,其中为电流比例器的输出,其实现电路如图3所示。

图3 Iout(i)ai/bi的电路实现
从上述分析可知,由式(3)可以确定输出电流Iout为n+1个内部输出电流的叠加,由式(7)~式(10)可以确定内部电流之间依次为积分关系,由式(14)可以确定其反馈通道是由n个电流比例器的输出电流和 Iout(0)依次反馈到输入端而构成,采用 MCCII实现的任意电流模式传递函数的电路如图4所示。
从模型的建立过程可以看出,整个滤波器模型是由电流积分器和电流比例器2类基本模块构成,因此只要能够实现电流积分器和电流比例器的有源器件均能实现任意的电流模式滤波器模型。因此该电路模型还可以采用OTA、CCC(current controlled current conveyor)、CFA(current feedback amplifier)等有源器件实现,因而该方法具有通用性。
3.2 滤波器模型参数的计算
根据MCCII的端口特性可以求出图4电路的传递函数:
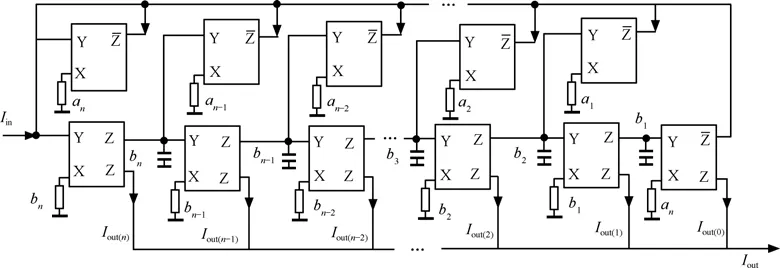
图4 基于MCCII的任意电流模式滤波器模型

其中,τi为积分器的时间常数,Ki为电流比例器的比例系数,可以分别表示为

将所需设计的滤波器的传递函数与式(15)相比较,即可以确定元件的参数值。
4 设计举例
采用该模型可以实现任意阶的电流型巴特沃斯、切比雪夫、椭圆滤波器,下面以三阶椭圆低通滤波器和六阶巴特沃斯通用滤波器为例来验证该模型的正确性。
4.1 三阶椭圆低通滤波器
由该模型实现的三阶椭圆低通滤波器电路如图5所示。其传递函数为

图5 三阶电流模式椭圆滤波器

根据式(16)、式(17)和图5可以确定

将时间常数τ 和比例系数K代入式(19)可以得到图5电路的传递函数:
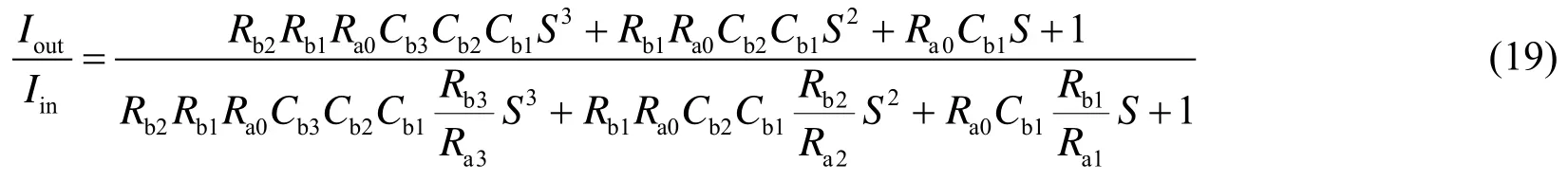
由文献[15]查阅到一个三阶椭圆低通滤波器的归一化传递函数:

由于该传递函数分子表达式缺一次项和三次项,根据前面分析可知,当取 Iout= Iout(0)+ Iout(2)时则可以实现椭圆低通滤波器。比较式(20)和式(19)可以得到

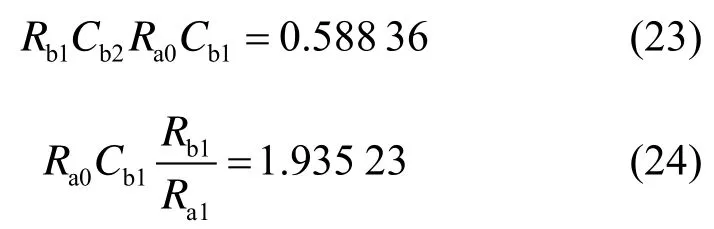
由式(22)和式(23)可以确定 Rb2/Ra2= 2 .4。取Ra0= Ra1= Ra2= Ra3= Rb1= Rb3= 1 kΩ,则 Rb2=2.4kΩ,并可以计算出归一化电容分别为=1.935×10-3F= 0.304F= 1 .178F ,取 fP=100kHz,则计算出反归一化电容 Cb1= 3080pF,Cb2=484pF,Cb3= 1875pF。
4.2 六阶巴特沃斯通用滤波器
六阶巴特沃斯通用滤波器的实现电路如图6所示,其传递函数为
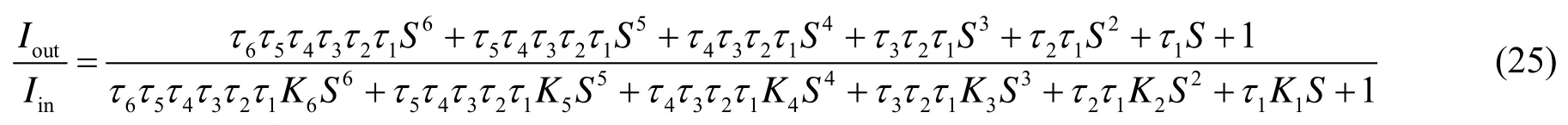
根据六阶归一化巴特沃斯滤波器传递函数的分母多项式
D(s)=s6+ 3 .8637 s5+ 7 .4641s4+ 9 .1416s3+7.4641s2+ 3.8637 s+ 1,取 fP=1MHz,令 K6= K5=K4=K3=K2=K1= 1 ,电路中所有的电阻均取1000Ω,按照上述相同方法将电容设置为


图6 六阶巴特沃斯通用滤波器
根据式(15),当输出电流 Iout= Iout(0)时,实现低通波器;当输出电流 Iout= Iout(3)时,实现带通滤波器;当输出电流 Iout=Iout(6)时,则为高通滤波器;当输出电流 Iout= Iout(0)+ Iout(6)时,可以实现带阻滤波器。当 Iout=Iout(6)-Iout(5)+Iout(4)-Iout(3)+Iout(2)-Iout(1)+ Iout(0)时电路则可以实现全通滤波器。
4.3 仿真分析
为了验证电路的可行性,分别对实现的椭圆滤波器和巴特沃斯滤波器进行PSPICE仿真,MCCII采用如图1所示内部电路,电源电压为±1.5V,VBS=0.5V,采用台积电0.35um COMS工艺参数[8]对滤波器的幅—频特性进行模拟后的结果如图7(a)、图7(b)虚线所示。
对椭圆滤波器的仿真结果进行测试得:fp=96.4kHz,与设计的截止频率100kHz相差3.6kHz,fs=121.5kHz,则ωs/ωp=1.26;通带纹波为1.42dB;阻带最小衰减量23.70dB。由传递函数式(15)可以计算出该椭圆型滤波器的理想性能参数如下:通带纹波为1.41dB,阻带最小衰减量为17.6dB,ωs/ωp=1.24。对巴特沃斯滤波器的测试结果为:带通滤波器的中心频率为889.5kHz,低通滤波器的截止频率为 889.1kHz,高通滤波器的截止频率为878kHz。
产生上述频率误差的主要原因是 MCCII器件端口的寄生参数(寄生电阻和寄生电容),根据文献[7],图1的MCCII器件X端口串联了一个约100Ω的寄生电阻RX,Y端口存在一个1.4pF的寄生电容CY,Z端口存在一个1.5MΩ的寄生电阻RZ和一个1.2pF的寄生电容CZ。为了减小寄生参数对电路的影响,在设计中可以将相应器件的寄生电阻和寄生电容分别折算到相应端口所接的电阻和电容值上。

图7 滤波器仿真结果
对于图5的三阶椭圆滤波器,将MCCII的寄生参数折算到相应的电容和电阻上,即 C1=3076pF,C2=480pF,C3=1873.8pF ,Ra0= Ra1= Ra2= Ra3=Rb1= Rb3= 0.9kΩ,Rb2= 2.3kΩ,重新对电路进行PSPICE仿真后的结果如图7(a)的实线所示,此时对应的截止频率为99.68kHz。类似的,对六阶巴特沃斯滤波器考虑器件的寄生参数后的仿真结果如图7(b)实线所示。经测试带通滤波器的中心频率为1.0MHz,低通滤器的截止频率为1.04MHz,高通滤波器的截止频率为0.974MHz。图7(c)为六阶巴特沃斯带通滤波器不同中心频率对应的幅频响应曲线,即将图6中所有的电阻分别设置为9.9kΩ、4.9kΩ、1.9kΩ、0.9kΩ和 0.4kΩ而电容维持不变所得到的幅频响应曲线。当电阻取上述参数并考虑电路的寄生参数,根据理论计算对应的中心频率分别为0.1MHz,0.2MHz、0.5MHz、1MHz和 2MHz,对图 7(c)的仿真结果进行测试,其中心频率分别对应为0.106MHz、0.204MHz、0.501MHz、1MHz和1.96MHz。从上述分析数据可以看出,当考虑器件的寄生参数后,滤波器的性能参数非常接近理想参数,从而可以证明提出的电路模型是正确的。在设计中为了减少寄生参数对电路性能的影响,在设置电路的参数时,电阻应远远大于器件X端口的寄生电阻RX,电容应远远大于相应端口的寄生电容。
5 结束语
本文通过对任意的电流模式传递函数进行数学分解,从而提出了一种可以实现任意阶任意类型的电流模式滤波器的综合设计模型,并采用MCCII为有源器件实现了具体的电路模型。通过对三阶椭圆滤波器和六阶巴特沃斯滤波器的设计和实验分析证明了该模型的正确性。采用该方法实现的滤波器电路与同类电路相比具有如下特点:1)系统性强,可以对任意一种电流模式滤波器进行综合设计;2)结构简单,n阶滤波器由(2n+1)个有源器件,n个接地电容和(2n+1)个接地电阻构成,有利于单片集成;3)在实现巴特沃斯滤波器时,可以通过对输出信号的选择实现多种滤波功能;4)高阻抗输出;5)实现的滤波器性能优良。因而提出滤波器模型可以在通信电路和电子测量系统中得到广泛的应用。
[1] SCHAURMANN R, VAN V M. Design of Analog Filter[M]. New York∶ Oxford Press, 2001.
[2] MINAEI S, YUCE E. Universal current-mode active-C filters employing only plus-type current controlled conveyors[J]. Frequenz,2006, 60∶134-137.
[3] WANG H Y, LEE C T. Versatile insensitive current-mode universal biquad implementation using current conveyors[J]. IEEE Trans on CAS(II), 2001,48∶409-413.
[4] FABRE A, SAAID O, WIEST F, et al. Low power current mode second-order bandpass IF filter[J]. IEEE Trans Circuits Syst II∶ Analog Digital Signal Process, 1997,44∶436-46.
[5] 石文孝,王树勋,韩庆全. 高输出阻抗多功能电流模式双二阶滤波器[J].通信学报, 2004, 25(6)∶95-101.SHI W X, WANG S X, HAN Q C. High output impedance multi-function current-mode biquad filter[J]. Journal on Communications, 2004, 25(6)∶ 95-101.
[6] TOKER A, OZOGUZ S, CICEKOGLU O, et al. Current-mode all-pass filters using current differencing buffered amplifier and a new high-Q bandpass filter configuration[J]. IEEE Transactions on Circuits and Systems-II∶ Analog and Digital Signal Processing, 2000,47∶949-954.
[7] HORNG J W, HOU C L, CHANG C M. High output impedance current-mode first-order allpass networks with four grounded components and two CCIIs[J]. International Journal of Electronics, 2006, 93(9)∶613-621.
[8] 王春华, 闫健卓, 沈光地. 基于 MOCCII 的多环反馈电流模式滤波器的系统设计[J]. 通信学报, 2002, 23(4)∶11-16.WANG C H, YAN J Z, SHENG G D. The systematic design of multiple-loop feedback current-mode filters based on MOCCII[J]. Journal on Communications, 2002, 23(4)∶11-16
[9] 彭良玉. 何怡刚, 黄满池等. 电流模式N阶CCCII-C低通滤波器的系统设计[J]. 电子学报, 2003, 31(8)∶1234-1236.PENG L Y, HE Y G, HUANG M C, et al. A systematic design of current-mode nth-order CCCII(±)-C low-pass filter[J]. Acta Electronica Sinica, 2003, 31(8)∶1234-1236
[10] CHANG C M, AL-HASHIMI B M. Analytical synthesis of current mode hight order OTA-C filters[J]. IEEE Trans on Circuits and System-I, 2003, 50(9)∶1188-1192
[11] 李志军,王春华,王仕果.基于MOCCCII-C的n阶电流模式滤波器[J].固体电子学研究与进展, 2006, 26(2)∶247-250.LI Z J, WANG C H, WANG S G. Nth-order current mode filter based on MOCCCII-C[J]. Research & Progress of SSE, 2006,26(2)∶247-250.
[12] YAN Y S, CHEN J J. New current mode all pole and elliptic filter employing current conveyor[J]. Electr Eng, 2007, 89∶457-459.
[13] JIRASEREE A, SURAKAMPONTORN W. Efficient implementation of tunable ladder filter using multi-output current controlled conveyors[J]. Int J Electron Commun (AEU), 2007, 61∶1-13.
[14] CHANG C M, AL-HASHIMI B M, CHUANG S Y, et al. New high-order current mode filter structures using only single-ended-input OTA and grounded capacitors[J]. IEEE Transaction on Circuits and System-II, 2004, 51(9)∶ 458-463.
[15] TU S H, CHANG C M, ROSS J N, et al. Analytical synthesis of current-mode high-order single-ended-input OTA and equal-capacitor elliptic filter structure with minimum number of components[J]. IEEE Transaction on Circuits and System-I, 2007, 54(10)∶2195-2210.

