基于预处理的单符号可译全分集准正交空时分组码设计
成文婧,刘伟,丁丁,魏急波
(国防科技大学 电子科学与工程学院,湖南 长沙 410073)
1 引言
空时编码技术能够充分利用 MIMO(multiple input multiple output)系统中多个独立的传输通路获得分集增益,从而大幅提高信息传输的可靠性,被认为是新一代移动通信系统的关键技术之一。正交空时分组码(OSTBC, orthogonal space time block coding)[1,2]不仅可以达到全分集,而且是单符号可译的,即每个发送符号可以彼此独立地进行最大似然(ML, maximum likelihood)译码,译码复杂度与星座调制阶数成线性关系。然而,当发送天线数大于 2时,复星座下的OSTBC码速率均小于1[2]。为提高传输速率,文献[3]提出了准正交空时分组码(QOSTBC, quasi-orthogonal space time block coding),该码可通过星座旋转[4]获得全分集,但需要使用成对符号联合ML译码,其译码复杂度与星座调制阶数的平方成正比。当发送天线数大于 4时,QOSTBC[3,4]的码速率仍然小于1。为此,文献[5,6]提出了分组可译的QOSTBC,码速率在任意发送天线数下都能达到 1。文献[7]系统研究了全分集QOSTBC的码速率、译码复杂度和分集阶数的最优折中问题,提出了 MGp-QOSTBC(multi-group decodable QOSTBC)构架,进一步完善了QOSTBC的理论研究。此外,文献[8]分析QOSTBC的等效信道矩阵特性,提出了一种基于预处理的发送策略,使QOSTBC可以实现单符号ML译码,但是该策略不能保证全分集,所以带来很大的性能损失[8]。
以上空时码[1~8],其码字元素取自于集合(z表示空时编码前的符号)。后i来文献[9,10]提出了一种更一般的 QOSTBC(G-QOSTBC),它扩大了码字元素的取值范围,让其元素取自更大的集合该码不但对任意的QAM星座都能达到全分集,而且不会带来星座图的扩展。但是这种码需要进行成对符号联合译码,译码复杂度较高。
本文从降低译码复杂度的角度出发,把预处理的思想应用于 G-QOSTBC中,使其能实现单符号ML译码。另外,设计合理的符号交织和星座旋转,在保证单符号ML译码的同时还达到了全分集和最大的编码增益。该编码方案的主要优势在于:与G-QOSTBC的性能几乎相近却具有更低的译码复杂度;与另一种全分集单符号可译码 CIOD (coordinate interleaved orthogonal design)[12]具有完全一致的误码率性能,但降低了峰均比。
符号说明:小写粗体表示向量,如r,矢量r的第k个元素表示为 rk;大写粗体表示矩阵,如H,矩阵H的第k列表示为 hk,矩阵H的第p行第q列的元素表示为 hp,q; Id表示大小为d的单位矩阵。(·)*、(·)T和(·)H分别表示对矩阵进行共轭、转置和共轭转置操作。det( )表示求矩阵的行列式。
2 系统模型
考虑发送天线数nT=4,接收天线数nR的MIMO系统,传输一个码字占用T=4个符号周期。系统模型如下:

假设 hp,q为准静态平衰落信道,它在一个码字时间内保持不变,在不同码字之间独立地变化。假设接收端完全已知信道状态信息,而发送端未知。
本文以下的设计都针对文献[10]提出的4× 4的G-QOSTBC,其码字如式(2)所示。
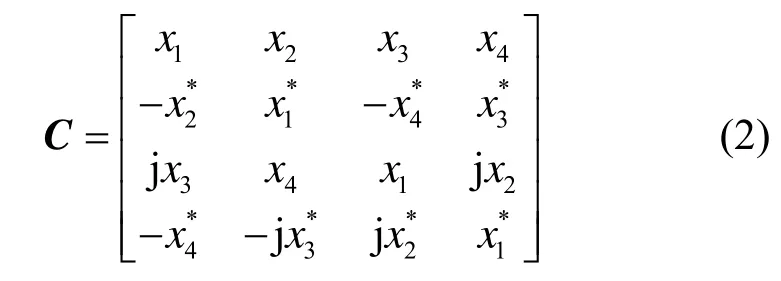
3 基于预处理的思想保证单符号最大似然可译
本节将从降低译码复杂度的角度出发,把预处理的思想应用于 G-QOSTBC中,推导基于预处理的单符号可译系统模型。
考虑接收天线数nR=1,联合式(1)和式(2),得到以下模型:
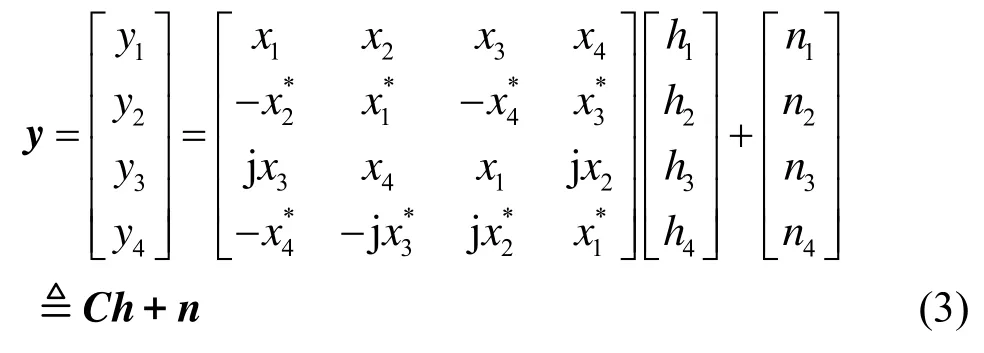
式(3)可等价变换为

其中, n′是对n的某些分量做共轭处理,所以 n ′为白噪声向量。
由式(4)可推得

由于HHH为Hermite矩阵,所以其特征值均大于等于0。因此其特征值分解可以表示为
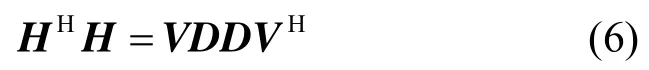
其中,特征向量矩阵V为常数矩阵,跟实际的信道无关(具体的分解过程参见附录1),这里给出结果。

假设接收端完全已知信道,所以在接收端可以对接收向量 y ′左乘 D-1VHHH有:
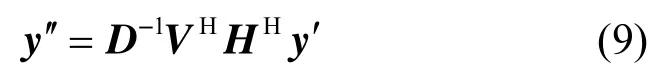
将式(4)和式(6)代入式(9)中,可得
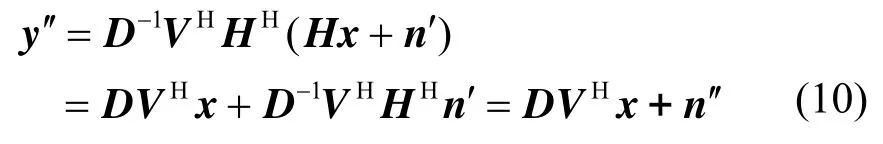
可以证明, n′为白噪声。证明过程参见附录2。
由式(10)可以看出,在发送端做一定的预处理,可以保证在接收端单符号可译。具体来说,由于特征矩阵V是和信道无关的常数矩阵,可以在发送端对星座映射后的符号做预处理如式(11)所示。

则得到单符号可译码系统模型为

此时,接收端最大似然译码等价为寻找(s1, s2, s3, s4)使ML度量

最小。由于D是一个对角阵,所以ML度量可以写成4个独立的度量之和的形式,即

4 全分集设计和最大化编码增益
第3节提出的基于预处理的G-QOSTBC可以实现单符号可译,但是本节后面分析表示,这种处理不能获得全分集。本节将在第3节的基础上,通过合理的符号交织(重新安排每个符号的实部和虚部)和星座旋转来获得全分集并最大化编码增益。
由式(2)可知,

其中,

则

将式(9)代入式(13)和式(14)有

所以,将式(16)和式(17)代入式(15)可得

定义任意2个码字之差为ΔC,则

当Δs1≠0,Δs2=Δs3=Δs4=0时,ΔC≠0,代入式(19)可得,此时 d et(Δ CHΔC ) = 0,也就是说基于预处理的G-QOSTBC不能保证对于 ∀ ΔC≠0都有 d et(Δ CHΔC)>0。所以该码是不能获得全分集的。

图1 发送端结构图
针对此问题,本文提出一种全分集的发送策略,具体处理流程如图1所示。其中是来自旋转星座 A = Aejθ的符号,经过符号交织和预处理后再进行 G-QOSTBC编码。通过合理地设计星座旋转角θ和符号交织,可以达到全分集同时保持单符号译码和最大化编码增益。前文已经介绍了预处理矩阵V的设计,本节后面将详细给出符号交织和星座旋转的方法。
把信号向量a中每个符号的实部和虚部重新组合,得到新的向量s如下:

其中 aiI表示 ai的实部, aiQ表示 ai的虚部,i= 1 ,… ,4 。
下面通过合理设计星座图来保证全分集和最大化编码增益。为此,首先给出文献[11]中对(CPD,coordinate product distance)的定义。
定义 1 对于任意 2个星座点 u = uI+ j uQ和v=vI+jvQ且u≠v,其CPD定义为:星座点集A的CPD为星座点集中任意 2个星座点的 CPD的最小值,即
将式(20)代入式(19)得到

此时 d et(Δ CHΔC)表达式中每个因式都包含a1, a2, a3, a44个符号的信息(实部信息或虚部信息)。当ΔC≠0时,Δ a1,Δ a2,Δ a3,Δ a4中至少有一个不为0。不妨假设Δa1≠0,Δ a2=Δ a3=Δ a4= 0 ,得到
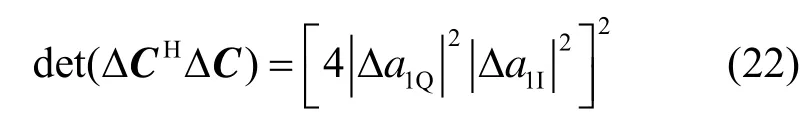
分析 d et(Δ CHΔC)的表达式(22),可以得到:设计星座A,使得 C PD(A)>0,ak∈A,k= 1 ,2,3,4,则可保证该码达到全分集。这是因为全分集需要满足 ∀ ΔC≠0都有det(Δ CHΔC ) > 0。根据式(22),只要就能保证 d et(Δ CHΔC ) > 0。也就是说,适当设计星座A使其 C PD> 0 ,则可以获得全分集。实际上将任意 C PD (A ) = 0的星座做一定的旋转θ即可保证其 C PD> 0 。
设计最优的旋转角θ,保证星座点集A的CPD最大,则可最大化编码增益。由式(22)可以看出,最大化编码增益即是使最大。这和最大化星座点集A的CPD是一致的。因而最优的旋转角应保证星座点集A的CPD最大。文献[11]中提出了一种全分集单符号可译码 CIOD,同样是利用最大化星座的 CPD来达到最大编码增益的。所以文献[11]中分析得到的 CIOD在不同类型星座下的最优旋转角同样适用于本文提出的空时码。例如,对于方形的 QAM 星座,其最佳的旋转角为arctan(2)/2。
至此,本节证明了通过合理设计符号交织和星座点集A,保证其 C PD> 0 ,且最大化此星座点集的CPD,则可以达到全分集和最大化编码增益。
文献[11]中得出,对于CIOD,其

与式(21)比较可以看出两者仅在系数上不同。但是本文的码利用了所有的空时单元,而CIOD只利用了一半的空时单元,所以式(23)中每个符号能量是式(21)中每个符号能量的 2倍,因此本文提出的码和CIOD具有相同的编码增益。然而,由于本文所设计的码利用了所有的空时单元,所以比CIOD具有更好的峰均比性能[11]。
由此,ML度量可以重写成f(a1)+f( a2)+f( a3)+f(a4)的形式,做单符号译码。

5 仿真结果
为了验证本文所提码的性能,本节对其性能进行了仿真分析,并与文献[10]提出的G-QOSTBC,文献[8]提出的基于预处理的QOSTBC,以及文献[11]提出的CIOD进行比较。调制方式为QPSK,其中G-QOSTBC采用的星座点集为CIOD以及本文提出的码都采用星座点集A = Aejθ,其中旋转角 θ = a rctan(2)/2。发送天线数nT= 4 ,且发送端能量归一化。信道为准静态平衰落Rayleigh信道,服从均值为0,方差为1的复高斯分布。
5.1 本文的编码方案的性能以及与其他码的比较
图 2给出了接收天线数nR=1和nR=2下的性能曲线。从图2可以看出,相比与文献[8]基于预处理的 QOSTBC方案,本文的编码方案在误码率为10-3,接收天线数为1和2时,分别约有3dB和1.3dB的性能增益。与CIOD相比,本文提出的码具有相同的性能且二者都可以实现单符号ML译码。但是CIOD一半的空时单元始终是 0,也就是说码字能量只集中在另一半空时单元上。而本文提出的码,码字能量分布在所有空时单元内,所以峰均比(PAR)较CIOD要低。相对于G-QOSTBC而言,本文的码仅有非常小的性能损失,这是由于编码增益有稍许降低。根据文献[4]对编码增益的定义可以推出,QPSK调制下,G-QOSTBC的编码增益为0.353 6,而本文所提的码的编码增益为 0.334 4,稍微低一点。但是,带来的好处是译码复杂度大大降低,特别是在高阶调制时,这种降低更为明显。

图2 4天线系统下基于预处理的QOSTBC、G-QOSTBC、CIOD以及本文的码的性能曲线
5.2 复杂度分析
以接收天线数目nR=1为例,对本文的编码方案和文献[11]提出的 G-QSTBC的译码复杂度进行分析。本文的编码方案可以单符号ML译码,对于M阶调制,其乘法次数为16M,加法次数为12M,比较次数为4(M-1)。G-QOSTBC需要成对符号联合译码,其乘法次数为 80M2,加法次数为 46M2,比较次数为 2(M2-1)。可以看出,本文方案的译码复杂度是和M成正比的,而G-QOSTBC的译码复杂度是和 M2成正比的。所以在同样阶数的调制方式下,单符号译码具有更低的复杂度。
表1~表3分别给出接收天线数为1时,不同调制阶数下单符号译码和成对符号译码的乘法次数,加法次数和比较次数。

表1 单符号译码和成对符号译码的乘法次数

表2 单符号译码和成对符号译码的加法次数

表3 单符号译码和成对符号译码的比较次数
5.3 峰均比分析
仿真时保证码字的平均功率等于 1,那么码字的峰均比等于其峰值功率。计算码字峰值功率时,需要考虑所有可能发送码字的所有空时单元的最大功率。例如,本文的编码方案中,信号向量中包含4个符号,每个符号采用M阶调制时,共有 M4个相异的信号向量。对于每个信号向量,做符号交织,预处理和G-OSTBC调制后,则得到 M4个相异的码字,每个码字都存在16个空时单元。通过计算机搜索的方法先找到每个码字的16个空时单元中的峰值功率,再比较所有 M4个码字的峰值功率的最大值,从而得到本文编码方案的峰值功率。
图3比较了本文的编码方案和CIOD在不同调制星座下的峰值功率。可见,该编码方案比 CIOD大大降低了峰值功率,从而降低了峰均比。
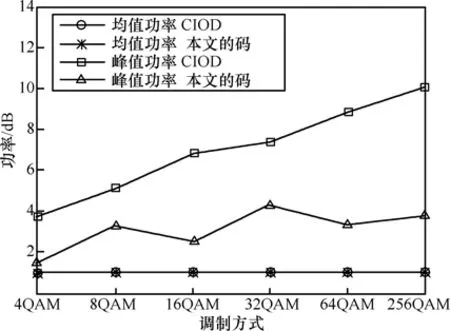
图3 4天线系统下CIOD以及本文的码的峰均比性能
6 结束语
本文主要从降低译码复杂度的角度出发,改进了文献[10]的 G-QOSTBC,提出了一种新的发送策略,该策略可以实现单符号最大似然译码,同时保证全分集和最大编码增益。该发送策略首先将比特信息做旋转星座映射,经过符号交织和预处理后,进行G-QOSTBC编码。它相对于G-QOSTBC仅有非常小的性能损失,但译码复杂度却大大降低,特别在高阶调制时降低得更为明显。通过分析得到,本文所提的码的最优旋转角和最大编码增益都与CIOD相同,目前4 4×CIOD在各种星座下的最优旋转角都可直接应用于本文所提的码。但是由于CIOD仅使用了一半的空时单元,所以本文所提的码比CIOD具有更低的峰均比。从另一方面而言,本文也说明:预处理方法结合适当的符号交织和星座旋转,不但能降低 G-QOSTBC的复杂度,而且还能达到全分集,因此推测这种方案对所有的QOSTBC都是可行的,同时这也是笔者进一步要研究的工作。
附录1 HHH的特征值分解推导

首先求HHH的特征值。
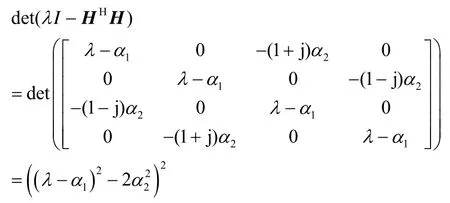
令其等于0,得其特征值为

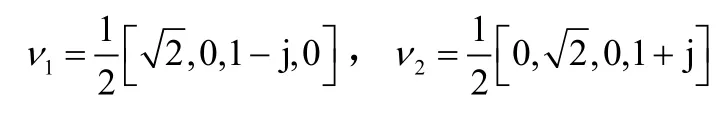
解方程组 (λ3I-HHH) x=0,求得其对应的特征向量为

则HHH的特征值分解表达式为 HHH= VDDVH
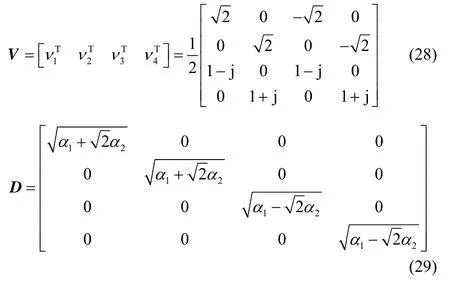
附录2 证明 ′′n为白噪声
奇异值分解定理[12]:若 A =(aij)N×N为满秩矩阵,λ1, λ2,… ,λN为AHA的特征值,则为A的奇异值,且A有如下的奇异值分解:其中 UA和 VA为N阶的酉矩阵,且分别为 A AH和 AHA的特征向量矩阵,
根据以上奇异值分解定理,则对 H做奇异值分解为H =UDVH,其中V和U为酉矩阵,V为HHH的特征向量矩阵,如式(7)所示。D为对角阵,其对角元素为HHH的特征值的平方根,如式(8)所示。
则n′= D-1VHHHn ′= D-1VH( UDVH)Hn ′= UHn′。由于 n′为白噪声,且U为酉矩阵,所以 n′为白噪声。
[1] ALAMOUTI S M. A Simple transmit diversity technique for wireless communications[J]. IEEE J Select Areas Commun, 1998, 16(8)∶1451-1458.
[2] TAROKH H J V, CALDERBANK A R. Space-time block codes from orthogonal designs[J]. IEEE Trans Inform Theory, 1999, 45(5)∶1456-1466.
[3] JAFARKHANI H. A quasi-orthogonal space-time block code[J]. IEEE Trans Commun, 2001, 49(1)∶ 1-4.
[4] SU W, XIA X G. Signal constellations for quasi-orthogonal space-time block codes with full diversity[J]. IEEE Trans Inform Theory, 2004,50(10)∶ 2331-2347.
[5] DAO D N, YUEN C, TELLAMBURA C, et al. Four-group decodable space–time block codes[J]. IEEE Trans Signal Processing, 2008, 56(1)∶424-430.
[6] KARMAKAR S, RAJAN B S. Multi-group decodable STBC from clifford algebras[J]. IEEE Trans Inform Theory, 2009, 55(1)∶ 223-231.
[7] KARMAKAR S, RAJAN B S. high-rate, multi-symbol decodable stbcs from clifford algebras[J]. IEEE Trans on Inform Theory, 2009,66(6)∶2682-2695.
[8] SEZGIN A, OECHTERING T J. Complete characterization of the equivalent MIMO channel for quasi-orthogonal space-time codes[J].IEEE Trans Inform Theory, 2008, 54(7)∶ 3315-3327.
[9] CHEN C Y, CHEN M Y, CIOFFI J M. Full-diversity quasi-orthogonal space-time block codes for M-PSK modulations[A]. Proc Globecom 2005[C]. St. Louis, MO, 2005. 3022-3026.
[10] CHEN M Y, CHEN C Y, LI H C, et al. Generally dimensional and constellation expansion free space-time block codes for QAM with full diversity[J]. IEEE Trans Inform Theory, 2006, 53(2)∶ 836-843.
[11] KHAN M Z A, RAJAN B S. Single-symbol maximum likelihood decodable linear STBC[J]. IEEE Trans Inform Theory, 2006, 52(5)∶2062-2091.
[12] HORN R A, JOHNSON C R. Matrix Analysis[M]. Cambridge University Press, 1999.

