多子阵对相干算法在高分辨率多波束测深系统中的应用研究

周天，李珊，李海森，刘晓

（1. 哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨 150001；2. 哈尔滨工程大学 水下智能机器人技术国防科技重点实验室，黑龙江 哈尔滨 150001)

1 引言

多波束测深系统自20世纪50年代问世以来发展至今，已成为当前海洋资源调查必不可少的重要设备之一。依据工作原理的不同可以分为：传统多波束测深系统和相干多波束测深系统。传统多波束测深系统采用常规的FT（fourier transform）波束形成技术，通过增加接收基阵的孔径（通常有上百通道）来提高海底回波方位估计的分辨率，此类系统的优点是在中央波束方向有很高的分辨率，但外侧波束方向分辨率低；相干多波束测深系统利用各通道接收波形的相位差对接收回波的每个时间样本进行到达方位估计，其通道数一般在2～6之间，此类系统在外侧波束方向能够得到高精度、高分辨率的方位估计，但其缺点是中央波束方位估计精度差。通过对比可以发现，两者的优缺点有着很强的互补性[1～3]。

因此，目前的研究热点集中在寻求将两者优点结合的信号处理方法，特别是关注基于传统多波束测深系统的多通道接收基阵，采用相干多波束测深系统中的基于相位信息的估计方法。Yang L在传统的分裂子阵相关器的基础上，提出了浅水应用场合下的多子阵相位检测法[4]；基于此算法，周天定量分析了多子阵划分与信噪比的关系[5]；Gerard基于相位估计误差最小准则推导了子阵间隔和子阵长度对相位估计精度的影响，并提出了三子阵相位估计算法，具有很高的实用价值，此算法中涉及了对子阵列间的相位差进行解2π模糊[6]；对此Sintes采用了经典的相位跟踪解模糊方法，但这种算法对地形和噪声太过于敏感，难以实际应用[7]；Gerard利用 Vernier方法解决三子阵优化结构引入的相位模糊[6]，但这种解相位模糊方法受噪声影响大，稳定性差[8～10]；Zhang Y L对Vernier方法进行了改进，进一步考虑了幅度和相位差曲线的连续性，提出了基于多元信息融合的相位差解模糊算法，提高了解相位模糊处理的准确性，但是这种方法涉及到幅度、相位差等判断门限的主观设置，并且涉及到区间内搜索，运算量大、不适合实时处理，限制了这种方法的实用性[11]。

本文针对相干算法中涉及的解相位模糊难点，提出了多子阵对相干算法，有效性强，适合多波束测深系统的实时实现，其性能在多次湖上实验中得到了充分的验证。

2 多子阵对相干算法

多波束测深系统中应用的各类相干算法都来自于传统的分裂子阵相关器，本文首先从分裂子阵相关器出发，推导应用相干算法的最优子阵结构模型，针对相干算法中常常存在的相位模糊，理论推导了相位模糊与子阵结构的关系，在此基础上推导提出多子阵对相干算法，用于高效准确地解决相干算法中存在的相位解2π模糊难点。

2.1 最优子阵结构模型

基阵模型如图1所示，基阵与水平方位夹角为α，整个基阵长度为L个阵元。

图1 基阵模型

设 θ0为 j号波束控制角，θ为海底回波到达角，d为阵元间距，子阵A、B长度为K个阵元，2个子阵声中心间距为M个阵元，N为FFT波束数。由基阵理论知2个子阵在θ0方位的相位差表达式为

为了得到最小的测向误差，对式(1)左右求导，得到

相干测量的相位差误差可以表示为[12]

其中，SNR为阵列的输出信噪比，不考虑阵元的指向性衰减，SNR与阵元输入信噪比SNRi的关系为

将式(3)和式(4)代入式(2)得到：

为了得到δθ的最小值，对上式求导得到

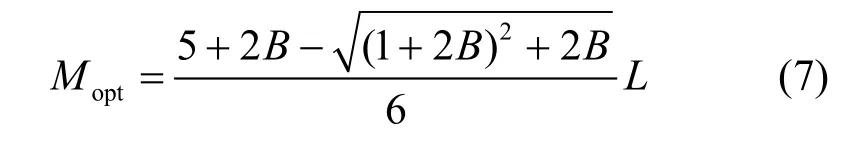
当全阵输出信噪比较高，即B很小时，得到子阵间距 Mopt≈2L/3，子阵长度 Kopt≈L/3。

将Mopt代入式(1)，得到A、B 2个子阵相位差：

以声呐系统中常采用的半波长布阵为例，式(8)中右边的第一项简化为，可见，如果要使得到的ΔφAB对应唯一θ角，必须要求。由于多波束测深系统采用的接收阵元数L很大，因此该条件不能满足，要想利用式(8)确定海底回波到达方位θ，必须要对相位解2π模糊。

2.2 解相位差模糊

目前广泛应用的相位解 2π模糊的方法为Vernier方法，其利用3个接收子阵组成2个相干子阵对来消除相位 2π模糊，其中每一个相干对的相位差测量可以表示为

mod(Δφ, 2π)表示含有相位模糊的相位差测量值，这样，每一个相干对测量得到的相位差都对应了几个波达方向 θ，但是实际中海底回波到达方向是确定的，2个子阵对观察到的海底回波方向也应该是相同的。如果把2个相干子阵对计算得到的回波到达角度的可能方向画出来，2个相互重合且属于不同的相干子阵对的回波到达方向才对应于真实的相位差值，因此满足式(10)的整数 n1、n2分别对应2个相干子阵对的相位模糊数。

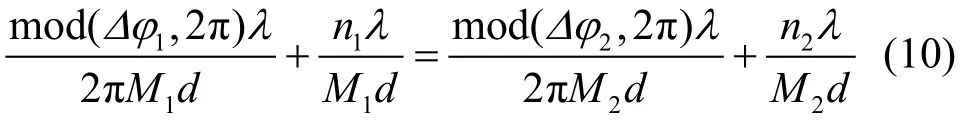
其中，M1、M2分别为2个子阵对中的子阵间距。

实际中，2个子阵对获取的到达角度不可能完全重合，在实际测量中要找的是在2个相干对中方位估计最接近的2个回波到达方向，使得式(11)中ε最小的n1和n2。

如果得到的ε大于Vernier有效门限，则很有可能对相位差的解模糊处理是错误的，因为此时由于噪声的存在不能分辨出真实的和错误的回波到达方向。为了提高 Vernier有效门限，可以采用大的子阵间距，但会导致 Vernier效率的降低，因此Vernier方法的缺点在于对噪声的敏感性，噪声的存在会大大降低算法的性能。

Zhang Y L在此算法的基础上，引入子阵波束输出的幅度信息作为门限设置的依据，并且进一步考虑了相位差序列的连续性，其并不在每个样本点上进行解模糊处理，而是对被“跳变点”划分出来的整个连续区域做相位解模糊处理[11]。因为在连续区域中的模糊数相同，因此可以将式(11)变为

对相位解 2π模糊就转变为在波束输出时间序列区间[t1，t2]中寻找n1和n2使得E最小。

这种方法提高了解模糊的准确性，但是它并不是针对每个样本点进行解模糊处理，而是需要在某个区间[t1，t2]内进行搜索，这种处理存在2个问题：①每个波束方向需要确定不同的[t1，t2]；②不便于工程实现，因为为了提高多波束测深系统的测绘ping率，要求测深算法运算时间尽可能要少，对于相干算法，必须要求在采样间隔内完成对当前样本的测向处理，否则，在采样结束后对全部样本进行统一处理的运算量将大大加重对硬件处理平台的压力。

本文提出的多子阵对相干算法，是一种高效准确、低复杂度的相位解 2π模糊方法，可以满足多波束测深系统实时实现的要求。

2.3 多子阵对相干算法

此算法解决相位模糊的出发点是首先推导出 2个子阵的相位差不存在 2π模糊的条件，然后在满足此条件的前提下，通过子阵结构配置解决子阵相位差模糊问题。

根据式(1)及模型，假设j号波束的波束宽度为θR，假设此时不存在相位模糊，将分别代入式(1)，根据形成非模糊区间的条件约束，得到：

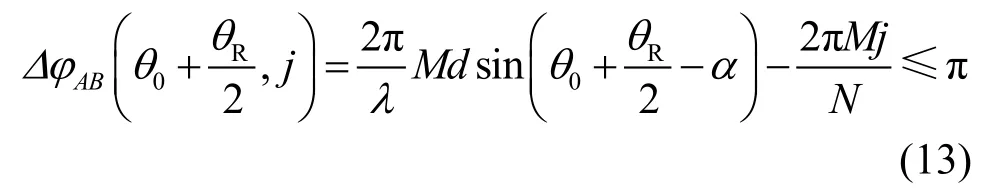
由式(13)和式(14)可得

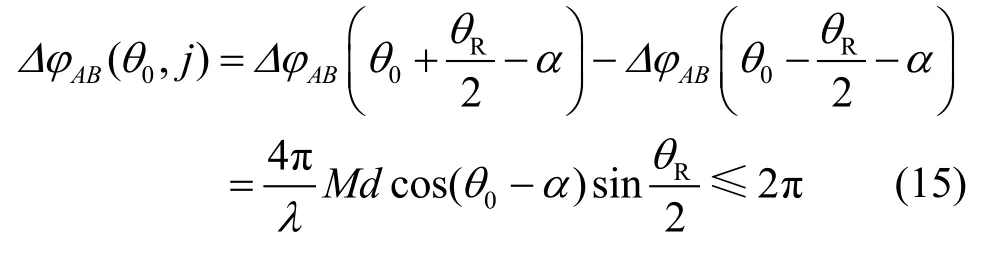
当子阵的孔径K较大时：

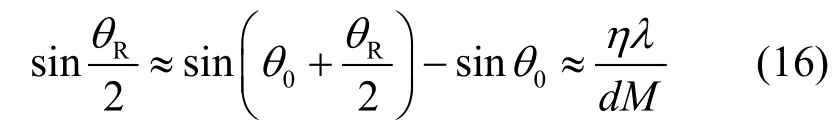
将式(16)代入式(15)得到，在保证形成非模糊区间的条件下，子阵阵元数K与子阵等效中心间隔M、波束号j之间应该满足的关系式为

在零号波束(j=0)、余弦加权(η=1.25)条件下，式(17)变成

由上面的分析可知，当2个子阵的间距满足式(18)时，其相位差不存在相位模糊，而2.1节中推导出的最优子阵结构不满足式(18)，本文提出的多子阵对解模糊的原理是在最优子阵结构基础上，利用2个子阵间的阵元构建额外的多个子阵，从而使得这些子阵结构满足式(18)的要求。

对于本系统采用的80个阵元的均匀接收线阵，按照2.1节中结论，2个子阵A、B的最优长度为26个阵元，间距为54个阵元，根据式(18)可知，其必然存在相位模糊。如果利用这 2个子阵间的 54个阵元构建额外的5个子阵C1、C2、C3、C4、C5。即共计A、C1、C2、C3、C4、C5、B这7个子阵，子阵中心坐标分别为[13，22，31，40，49，58，67]，每个子阵长度为26，相邻子阵间距为9，满足式(18)。由分析可知，虽然A、B间存在相位模糊，但是 7个子阵相互间不存在相位模糊。因此，为了得到待求的子阵A、B间无相位模糊的相位差值，可以利用 φAC1+ΔφC1C2+ΔφC2C3+ΔφC3C4+ΔφC4C5+ΔφC5B得到，与直接求φAB相比，回波样本采样间隔内所增加的运算量仅是5个复共轭相乘，比Vernier算法运算量更小、且更有效。

3 实验数据处理

3.1 多子阵对相干算法解模糊性能验证

实验使用的数据为利用自研的多波束测深系统采集的松花湖湖底数据，实验系统工作频率为300kHz，采用“T”型组合声学基阵，发射基阵为多元弧阵，接收阵为由80个阵元组成的均匀线阵，阵元间距为半波长。按照2.1节中推导的最优子阵结构，2个子阵间距为 54，子阵长度 K=26，采用2.3节中的新算法，将2个子阵间的54个阵元进一步细化分为5个子阵，则80个阵元共划分成7个子阵，相邻子阵间距M=9。

图3给出的是利用文献[6]中的Vernier解模糊方法，对 63°方向的波束输出序列进行处理得到的结果，从图中可以看到很多“斑点”，这些斑点不可以用于深度的估计，它的影响类似于严重的噪声干扰，必须加以剔除；图4中所示的即为利用多子阵对算法解模糊的结果，与图3相比，解模糊效果明显改善；图5为在图4的基础上，进一步对子阵输出序列进行滤波得到的结果，能够得到清晰的相位差曲线，需要指出的是，滤波固然可以降低噪声的影响，但也降低了距离分辨率。

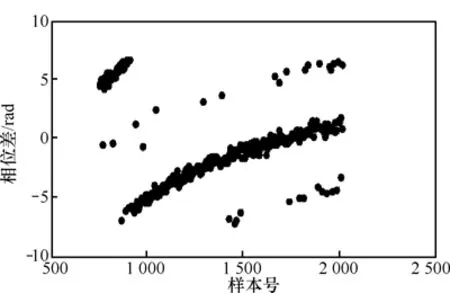
图3 使用Vernier方法的解模糊结果

图4 使用多子阵对方法的解模糊结果

图5 基于子阵滤波输出的多子阵对方法的解模糊结果

3.2 多子阵对相干算法测向性能验证

为了进一步验证此算法的实用性能，本文在消声水池进行了算法性能的测试实验。实验系统及多子阵结构同上。用于基阵测试的水池为六面消声水池，受测基阵和发射换能器相距11m，均位于水下3m处，水听器采用SMHP1997-07标准水听器。被测基阵安装在可旋转的升降杆上，基阵辐射面面向测量水听器。接收阵测量时，利用自动旋转装置使接收阵从-80°转到80°，转动速度为0.5°/s，在每个角度点上声源发射脉冲长度0.5ms，采样率40kHz，测量各个阵元输出。测试系统如图6所示。

图6 水池实验场景

图7 利用FFT算法和多子阵对相干算法对水池实验数据处理的结果

图 7为实验数据处理结果，图 7(a)为利用 80通道原始数据的常规 FFT波束形成输出，图 7(b)为利用 80通道原始数据的多子阵对相干算法处理的结果。数据处理结果验证了接收基阵可靠的束控性能以及多子阵对相干算法的有效性。对比图7可以看出，由于FFT波束形成的方位估计性能取决于波束输出的幅度特性，对于外侧波束方向的回波，接收阵有效孔径减小，导致波束变宽，方位估计精度下降；而多子阵对相干算法的方位估计性能依赖于波束输出的相位特性，在中央波束方向和外侧波束方向能同时获得高精度方位估计特性，相比于传统FFT波束形成算法优势明显。

3.3 湖底地形测量

为了考核算法的有效性，于2009年11月于吉林松花湖区进行了此多波束测深系统的航行实验[13]。实验湖区水深约56m，实验系统及算法采用的多子阵结构同上。选取某ping数据文件进行处理，起始记录时刻为第n0=3 000个采样时刻，传统的FFT波束形成算法与本文提出的多子阵对相干算法处理结果如图8所示。

图8 利用FFT算法和多子阵对相干算法对湖实验数据处理的结果

图8(a)为常规FFT波束形成输出，可以看到，在外侧波束方向波束变宽，导致分辨率变差。图8(b)由于采用了多子阵对相干算法，不仅在中央波束方向而且在外侧波束方向都能够得到高分辨率的回波方位估计结果，反映水下地形的关系曲线清晰可见。从图8(b)中可以清楚看出，采用此算法，可以实现水深60m下有效测绘条带达到了6倍覆盖，已经超过了和本系统工作频率和基阵形式相同的国外同类系统中的典型代表EM3000S。

4 结束语

相干测深算法是提高多波束测深系统分辨率和覆盖性能的重要保证，为了得到最小误差的子阵相位差估计而采用的最优子阵结构会导致子阵间的相位差存在相位模糊，传统 Vernier方法的性能受噪声影响大，这严重影响了海底地形探测的有效性。为此本文提出了多子阵对相干算法，不仅高效解决了多波束相干测深算法中的相位解模糊难点，而且有效提高了海底地形估计的分辨率和覆盖能力。克服了传统多波束测深算法海底采样不均匀的问题，具有很强的海底微地形探测能力。此算法已工程应用于国内首台多波束测深系统，其性能已得到了多次湖上实验的验证。

[1] 谭良, 全小龙, 张黎明. 多波束测深系统及其在水下工程监测中的应用[J]. 全球定位系统, 2009, 33(1)∶ 38-42.TAN L, QUAN X L, ZHANG L M. Application of multi-beam sounding system in underwater surveying[J]. GNSS World of China, 2009,33(1)∶ 38-42.

[2] 么彬. 多子阵波束域高分辨水声成像技术研究[D]. 哈尔滨工程大学, 2009.YAO B. Study on Multiple Sub-array Special Module Underwater Acoustic Imaging Technology[D]. Harbin Engineering University, 2009.

[3] 李成刚, 王伟伟, 阎军. 传统多波束系统与具有相干特点的多波束系统的研究[J]. 海洋测绘, 2007, 27(2)∶ 77-80.LI C G, WANG W W, YAN J. The study on traditional multibeam and interferometric multibeam[J]. Hydrographic Surveying and Charting.2007, 27(2)∶ 77-80.

[4] YANG L, TAXT T. Multbeam sonar bottom detection using multiple subarrays[A]. OCEANS’97[C]. Halifax, Canada, 1997. 932-938.

[5] 周天. 超宽覆盖海底地形地貌高分辨探测技术研究[D]. 哈尔滨工程大学, 2005.ZHOU T. Research on Techniques of Super Wide Coverage Seafloor Bathymetry and Physiognomy Detection[D]. Harbin Engineering University, 2005.

[6] LLORT-PUJOL L, SINTES C, LURTONT X. A new approach for fast and high-resolution interferometric bathymetry[J]. IEEE Oceanic Engineering Society Newsletter, 2006, (11)∶ 12-18.

[7] SINTES C. Deconvolution Bathymétrique D'images Sonar Latéral Par Des Méthodes Intérférométriques et de Traitement de L'image[D].Universite de Rennes I, 2002.

[8] SINTES C, SOLAIMAN B. Interferometric sides scan sonar and data fusion [J]. Proceedings of SPIE, 2000, (4051)∶ 149-157.

[9] SINTES C, SOLAIMAN B. Strategies for unwrapping multisensors interferometric side scan sonar phase[A]. Ocean’s 2000. MTS/IEEE[C].USA, 2000.2059-2065.

[10] LLORT-PUJOL G, SINTES C, GUERIOT D. Analysis of vernier interferometers for sonar bathymetry[A]. OCEANS’08[C]. Quebec,2008.

[11] ZHANG Y L, LI H S. An improved method for unwrapping phase difference in bathymetry[A]. ICIA 2010[C]. Harbin, 2010.1071-1075.

[12] GLYYN J M. Acoustic Calibration and Bathymetric Processing with Klein5410 Sidescan Sonar[D]. New Hampshire University, Burnaby,B S E E, UK, 2007.

[13] 李海森, 陈宝伟, 么彬等. 多子阵高分辨海底地形探测算法及其FPGA和DSP阵列实现[J]. 仪器仪表学报, 2010, 28(4)∶281-286.LI H S, CHEN B W, YAO B, et al. Implementation of high resolution sea bottom terrain detection method based on FPGA and DSP array[J]. Chinese Journal of Scientific Instrument, 2010, 31(2): 281-286.