基于降维循环谱的特征提取与目标识别

陈昌云， 刘 刚， 姬红兵， 游屈波

（①信息综合控制国家重点实验室，四川 成都 610036；②西安电子科技大学 电子工程学院，陕西 西安 710071）

0 引言

在日益复杂的电磁环境下，由于信号种类多、调制方式多样，使得提取信号的有效特征变得相当困难。因此，如何提取有效特征是解决目标识别难题的一个关键。

研究表明，传统的基于时域方法已经难以解决复杂电磁环境下的目标识别，因此，近年来许多研究人员都致力于其它变换域的特征提取方法，如“时——频”域，并取得了丰富的成果[1-2]。但是，时频分析方法仍存在着自身的不完善性，如短时傅立叶变换（STFT）难于兼顾时间和频率的精确度、Wigner-Ville分布无法消除交叉项的影响等，使得时频分析方法在目标识别中难于取得令人满意的结果。

通过对目标信号的分析，发现它们虽呈现非平稳性，但却具有循环平稳性。由于循环谱针对的是循环平稳信号，因此，循环谱在分析此类信号方面具有很大的优越性，它不是在“时——频”域检测目标信号，而是将信号转换到“频——频”循环域进行分析，体现了信号的谱相关在不同循环频率下的特性。目前，虽然已有研究人员把循环谱应用于目标信号检测领域，但是也只限于信号的检测和分离，并没有应用于特定目标信号的识别。此外，如何有效地解决循环谱的高维问题，仍是一个挑战。因此，本文提出了降维循环谱的目标识别方法，该方法以循环谱的相同频率点在不同循环频率下的相关性作为识别特征，并用主成分分析方法对该特征降维。实验结果表明，本文提出的目标识别方法具有很好的鲁棒性。

1 降维循环谱

1.1 循环谱

假设预处理后的目标离散信号为x(n)，那么其循环自相关函数为[3]：

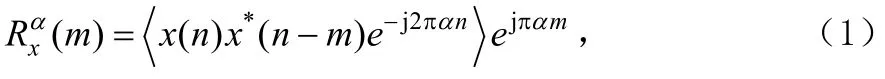
由此可知，循环自相关函数体现了循环平稳信号的频移相关性。另外，离散信号的循环谱定义为：

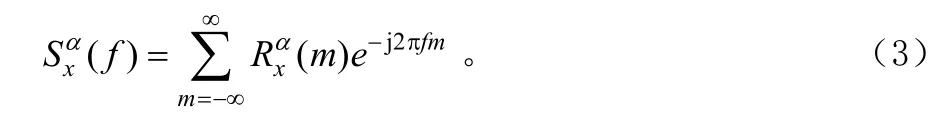
由式（1）和式（3）可知，当0=α时，式（1）和式（3）就转变成传统的自相关函数和功率谱函数。相对比传统的功率谱，它具有三个特点：一是循环谱具有信号可辨识能力；二是循环谱比传统的功率谱包含更多的信息；三是循环谱揭示了循环平稳信号的本质。另外，由于循环频率α的存在，使得循环谱包含更多描述目标信号的细微特征，为实现信号的细微特征提取提供了帮助。然而，在实际截获的信号中，其观测时间均是有限的，因此，在计算循环谱时，目前有两种近似估计方法[4-6]：时域平滑法和频域平滑法，虽然两种方法都是对循环谱的近似估计，但是时域平滑法比频域平滑法的计算效率要高得多。因此，本文采用时域平滑法对循环谱进行近似估计。

1.2 特征提取

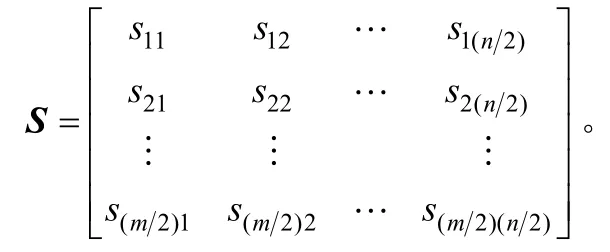
然而，循环谱S中的不同行向量并不是都能表征信号，有些行向量不仅含有大量的冗余信息，而且把这些行向量作为特征还会造成最终的分类错误，因此，这里采用Fisher判别率[7]（Fisher’s Discriminant Ratio,简称 FDR）来定量描述循环谱S中不同行向量特征对信号个体的可分类能力。假设循环谱S中的第l行为 s(l)，那么以 s(l)作为特征的Fisher判别率定义为：

式（4）中，C表示训练样本的总类别数；l=1,2,…,m/2；和分别表示训练样本中以s(l)作为特征时的第i类信号的均值与方差，FDR(s(l))表示以 ()sl作为特征时对所有类的可分类能力大小。FDRs(l)越大，表示特征s(l)对信号的可分类能力越强，通过设置门限，选取前p个最大的Fisher判别率所对应的特征构成特征集 Z(k),k=1,2,…,p，并且特征集Z(k),k=1,2,…,p中的特征矢量按所对应 Fisher判别率的大小进行排列。

当信号长度较长时，即n值较大，那么信号的循环谱维数较高，导致所提取的特征维数也较高，另外提取的特征中还包含了影响分类的冗余信息，因此，对提取的特征还需进行降维处理。目前，常用的降维方法主要有两种：主成分分析（Principle Component Analysis，简称PCA）和线性判别式分析（Linear Discriminant Analysis，简称LDA）。PCA是一种线性映射方法，它侧重于信号的重构以及最大限度地保留原信号的重要信息；而 LDA主要是侧重于特征的提取与分类，它没有考虑信号的重构、噪声的抑制以及可能丢弃零空间中对识别有用的分类信息，另外LDA还不可避免的遇到“小样本”问题。因此，本文采用PCA的方法对特征矢量进行降维处理。其算法流程如下[8]：

对测试样本提取降维循环谱特征集，可直接用变换矩阵W与测试样本相乘。在得到测试样本降维循环谱特征集后，还要对其进行分类识别。

2 实验结果及分析

选取类内相差较大、类间相近并且调制类型相同、载频相近的9类目标信号，每类30个样本，然后从每类中随机选取10个样本作为训练集，把每类剩下的20个样本作为测试集。（注：以下四个实验除特别说明外，均采用径向基函数参数为1的SVM做分类器。）

实验一：分析FDR值与识别率的关系。

采用特征 ()sl（l=1,2,…,m/2）来表征信号时，采用SVM对测试样本集进行分类，分别做100次蒙特卡罗的实验结果如图1所示。

图1 FDR值与识别率之间的关系

通常情况下，FDR值越大，与之相对应的特征对信号分类能力越强。从图1实验结果的总趋势可知，FDR值在增大，其识别率也在增大；另外，从图1还反映出，FDR值越小所对应的识别率较低，这说明其对应的特征不利于分类，因此，通过设置门限来选取前p个最大的FDR值所对应的特征构成特征集Z(k),k=1,2,…,p。

实验二：分析融合特征对识别结果的影响。

本实验分析通过融合特征集Z(k),k=1,2,…,p中不同的特征以分析特征融合对识别结果的影响。这里分别以(Z(1)，Z(2)),(Z(1),Z(2),Z(3)),…,(Z(1), Z(2),…,Z(p))作为特征（注：这里的特征是未经过PCA降维处理的），采用SVM对主成分特征分量分别做100次蒙特卡罗的识别结果如图2所示。从图 2 结果可知，以(Z(1)，Z(2)),(Z(1),Z(2),Z(3)),…,(Z(1), Z(2),…,Z(p))作为特征的识别结果与未经过 PCA降维处理Z(1)的识别结果相近，说明了Z(1)在融合特征进行分类时占据主导作用，由此反映出特征Z(1)包含了最能表征信号的细微信息。因此，实验三、四均是以特征Z(1)作为识别特征分析了降维处理以及选择不同分类器对识别效果的影响。

实验三：分析降维处理对识别效果的影响。

从实验二可知，以Z(1)（如图3所示）作为特征时可以获得较好的识别效果。但是从图3可看出，Z(1)不仅维数过高，并且含有大量冗余信息（即幅值近似为零的点），这些冗余信息不仅增大了后续分类的计算量，而且还削弱了特征Z(1)表征信号的能力，因此，这里采用PCA进行降维处理，提取特征Z(1)的主成分分量。这里取0.99η=时，Z(1)经PCA降维后变为只有 160维的特征，这里对比分析未经过 PCA降维处理的特征Z(1)和经过PCA降维处理后，采用SVM分别进行100次蒙特卡罗的识别结果是未经过PCA处理的平均识别率为85.7%，而经过PCA处理后则达到93.2%的识别率。由此可知，经过 PCA降维处理后，提高了识别率。这是由于经过 PCA处理后，只保留特征 Z(1)中的主成分特征分量，剔除了特征中的冗余信息以及抑制了噪声的影响，从而提高了识别率。

图2 融合特征与识别率的关系

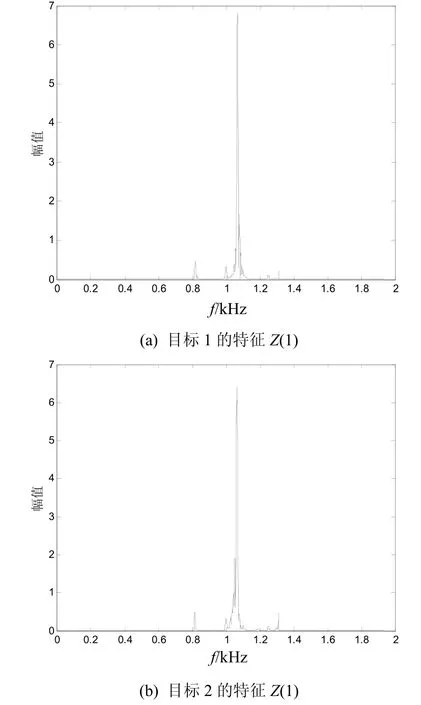
图3 不同目标的特征

实验四：选择不同分类器对识别结果的影响。

这里分析目前比较常用的两个分类器：神经网络和SVM。以Z(1)经过PCA降维处理后的特征作为识别特征，分别采用概率神经网络（PNN）和SVM进行100次蒙特卡罗的识别结果是 PNN取得了 81.7%的平均正确识别率，而 SVM则达到93.5%的正确识别率。可知，在相同特征的条件下，SVM的分类能力优于 PNN。另外，也说明了本文提取的特征能很好的表征信号，而且经过PCA处理后不仅降低了特征的维数，还剔除了冗余信息对分类结果的影响，最后结合SVM取得了较好的识别效果。

3 结语

本文提出了基于降维循环谱的特征提取与目标识别方法。该方法先采用循环谱对信号进行处理，从而在一定程度上抑制了噪声的影响。然后采用 Fisher判别准则进一步提取信号循环谱中的最优特征。针对最优特征中存在的冗余信息，最后采用PCA提取其主成分分量实现对最优特征的维数约减，并结合SVM实现了识别。通过实验表明，该方法所提取的信号特征不仅可以很好的表征信号，还具有较好的识别效果，从而也说明了本文方法的可行性和有效性。

[1] 解文斌.脉冲信号的特征分析和目标识别研究[D].合肥：国防科技大学硕士论文,2003.

[2] 赵拥军,黄洁.雷达信号细微特征时频分析法[J].现代雷达,2003(12):26-28.

[3] 黄知涛,周一宇,姜文利.循环平稳信号处理及应用[M].北京：科学出版社,2006.

[4] Brown W A,Loomis H H. Digital Implementations of Spectral Correlation Analyzer[J].IEEE Trans Signal Processing, 1993，41(02):703-720.

[5] Roberts R S,Brown W A,Loomis H H.Computationally Efficient Algorithms for Cyclic Spectral Analysis[J].IEEE Signal Processing Mag.,1991,8(02):38-49.

[6] 黄奇珊,彭启琮,路友荣,等.OFDM信号循环谱结构分析[J].电子与信息学报,2008,30(01):134-138.

[7] Theodoridis S, Koutroumbas K.模式识别[M].第3版.李晶皎，王爱侠，张广渊,等译.北京：电子工业出版社，2006.

[8] Kim K I,Kim H J.Face Recognition Using Kernel Principal Component Analysis[J].IEEE Signal Processing Letters,2002,9（02）：40-42.