相关对数阴影信道条件下基于贪婪的最优感知节点集合选择算法

张晓，王金龙，吴启晖

（解放军理工大学 通信工程学院，江苏 南京 210007）

1 引言

固定的频谱分配策略虽然可以有效保证系统的服务质量（QoS），却造成了频谱资源的巨大浪费。随着无线业务的迅速发展，频谱资源日益紧张，开放的频谱分配策略日益引起人们的重视。认知无线电技术在保证主用户服务质量的条件下以“动态接入”的方式利用主用户的空闲频段，大大提高了频谱的使用效率，是解决“频谱匮乏”问题的有效方法[1～3]。由于认知用户需要实时地、可靠地对主用户信号进行探测，以发现频谱空穴和避免对主用户的干扰，因此高可靠性的频谱感知技术是认知无线电存在的前提和基础。认知系统的感知性能主要由虚警概率 pf=p(H1/ H0)和漏检概率 pm=p(H0/H1)这2个性能参数来衡量，其中，H0代表主用户不存在，H1代表主用户存在。漏检概率决定着认知用户对主用户的干扰程度，虚警概率则影响着认知用户使用主用户频谱的效率[4]，因此认知系统一般都会对这2个性能参数进行约束，即规定认知系统在频谱感知时的漏检概率与虚警概率的上限[5]。

文献[6～8]指出单感知节点的频谱感知性能极易受到无线信道中阴影效应与多径衰落的影响而恶化，为了解决这个问题，人们提出了多认知用户合作谱感知的方法。合作谱感知是指认知网络的基站收集多个认知用户的感知结果进行融合判决的频谱感知方法，由于充分利用了多个认知用户的感知结果，有空间分集增益存在，因此合作谱感知方法可以极大地提高系统的感知性能[9～12]。文献[13,14]分析了合作谱感知方法在独立和相关信道条件下的频谱感知性能。在相同的pm约束下，pf会随着合作节点数的增加而减小，当合作节点数趋于无穷且节点间相互独立时，pf趋于零，节点间相关时，pf有一性能下限。虽然从系统的感知性能角度来看，合作感知节点数越大越好，但是在感知过程中的系统资源的消耗也渐近随合作节点数的增加呈线性增加，因此需要对合作节点数的选择进行折中，即在合作节点数的选择上没有必要追求系统的极限性能，只要满足系统对虚警概率和漏检概率的性能约束即可。本文提出的折中方法是在满足系统对虚警概率和漏检概率的性能约束的条件下用最少的感知节点来进行合作感知，从而使在感知过程中的系统资源消耗最小化。

在相关对数正态阴影信道条件下，感知节点之间的相关性会严重影响感知节点集合的感知性能，这是因为感知节点之间的相关性越大，感知节点之间的冗余度就越高，感知节点所带来的有用信息就会越少，因此怎样用最少的合作感知节点来满足系统对虚警概率和漏检概率的性能约束就变成一个值得研究的问题。文献[15,16]提出了一种简单的基于半径消除的感知节点集合选择算法，其主要思想是从认知网络中去掉与认知网络基站距离小于半径rc的认知节点，并用剩余的节点组成感知节点集合来进行合作感知，同时通过调整rc以使所选的感知节点集合满足感知性能约束。但是该算法仅仅通过简单地“挖洞”方法选择感知节点集合，并不能保证所选择的感知节点集合内的感知节点之间具有最小的相关性（例如半径rc外2个节点的距离非常近），因此也就不能保证该感知节点集合在满足系统感知性能约束的条件下具有最小的感知节点数目。

本文主要分为6节：第2节给出了本文所用的系统模型；第3节推导了感知节点集合的虚警概率性能上限；第4节给出了最优感知节点集合的定义以及所要满足的条件，并在此基础上提出了一种最优的选择算法，最后在贪婪算法的基础上提出了一种最优感知节点集合的次优选择算法，它可以以较低的计算复杂度得到最优感知节点集合的近似最优解；第5节是仿真分析；第6节是结束语。

2 系统模型

系统模型如图1所示。假设一个有n个认知用户的认知网络 Ωn，各认知用户用 ui（i=1,2,…,n） 来表示，随机分布在一个L×L的正方形区域内，区域中心与主用户发射机PT（例如电视发射塔）之间的距离为r。图中，Rp为主用户覆盖范围，由主用户发射功率决定；RG为保护间隔，由认知用户发射功率决定。 R=Rp+RG，如果r大于R，认知用户可以接入该频段，因此对于认知网络来说，谱感知问题转变为判定对于任意δ＞0，r=R+δ是否成立[13]。

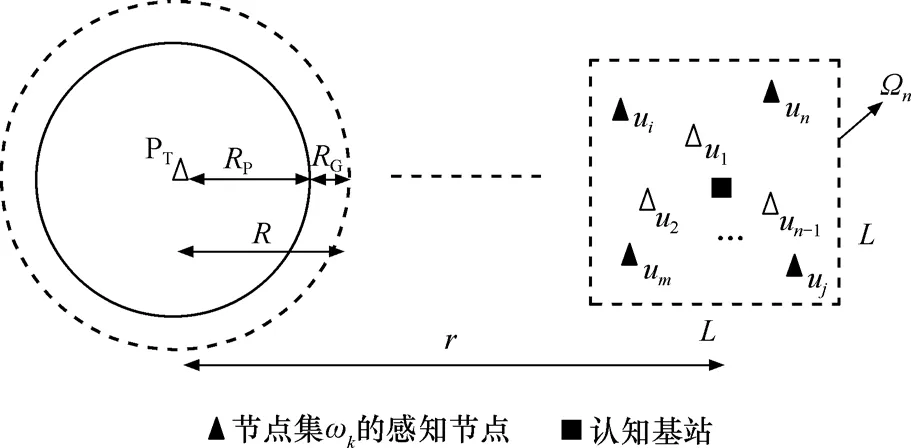
图1 系统模型

图中kω表示由从认知网络Ωn中选出的由k个认知用户组成的满足系统对虚警概率和漏检概率的性能约束的感知节点集合，kω采用合作谱感知协议来检测主用户的信号传输。为分析方便，假设L＜＜r，此时Ωn中不同的认知用户经历相同的路径损耗。定义yi为kω中第i个感知节点接收主用户信号的对数域信噪比(SNR dB)，则在对数正态阴影条件下，yi服从高斯分布，均值为µ（r），方差为2σ。这样，合作谱感知问题可以由下面的二进制假设检验模型来描述[13]：

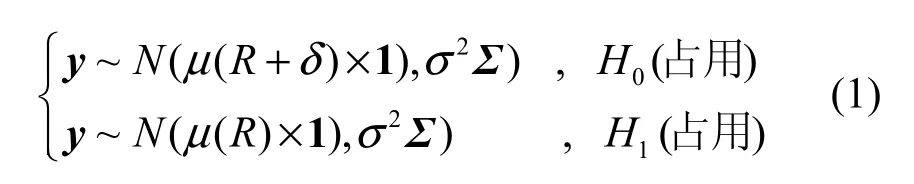
其中， y=[y1,…,yk]T，表示ωk的接收信噪比矢量；

1=[1,1,…,1]T是单位矢量；Σ 表示矢量y的k×k

k×1阶标准协方差矩阵。

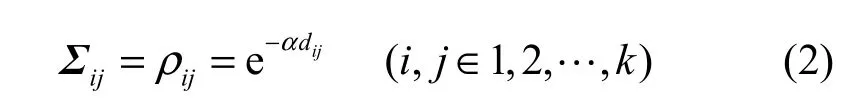
本文采用文献[14]提出的指数相关模型来对相关对数正态阴影进行建模，则协方差矩阵Σ可表示为dij表示感知节点集合ωk中节点i与j之间的距离；α是传播常数，由具体的传播环境决定，一般在市内环境中α≈0.12，在郊区α≈0.002。本文假设已知认知网络Ωn中各认知用户的位置（可以通过GPS或UWB等定位技术得到），则Ωn中各认知用户之间的距离也是已知的。

如第1节所述，认知系统的感知性能主要由虚警概率和漏检概率这 2个性能参数来衡量，因此FCC对这2个性能参数设定了严格的性能约束，例如在世界上第一个认知无线标准IEEE 802.22中规定认知用户必须保证pf≤0.1和 pm≤0.1[5]。本文假设认知用户必须保证pm≤β和pf≤γ。

3 感知节点集合的感知性能分析

3.1 软信息合并检测性能

由文献[13,14]可知，对于式（1）所表示的二进制假设检验问题的最佳软信息合并检测性能可以由基于似然比检验的Neyman-Pearson定理得到，其判决式为

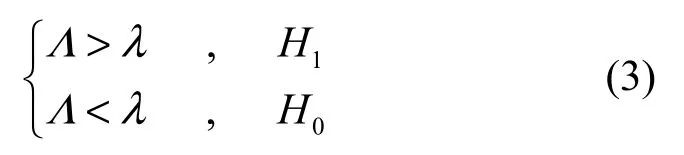
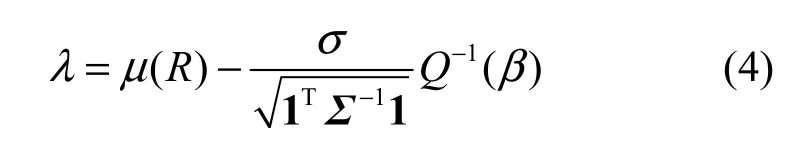
进一步可得虚警概率的表达式为[13,14]

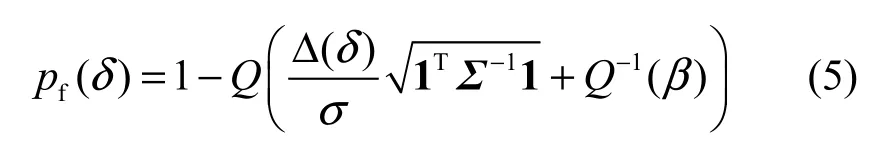
3.2 感知节点集合的虚警概率上限

设用dmin表示认知网络Ωn中任意 2节点之间距离的最小值，dij表示感知节点集合kω中任意两感知节点i与 j之间的距离，则存在以下关系：

由文献[17,18]可知感知节点之间的距离越小，感知节点之间的相关性就越大，感知节点集合的感知性能就越差，因此有：

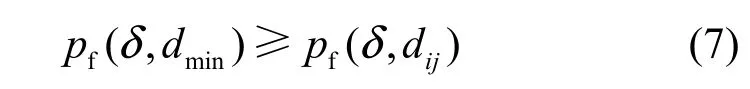
其中， pf(δ,dij)表示感知节点集合ωk的虚警概率；pf(δ,dmin)表示感知节点集合ωk中感知节点间距离均为dmin时ωk的虚警概率，此时协方差矩阵∑可以表示为

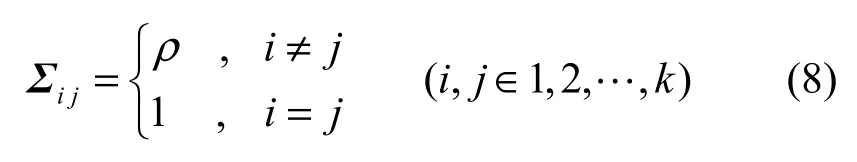
其中，ρ=e-αdmin。此时∑是对称Toeplitz矩阵，其逆矩阵可表示为

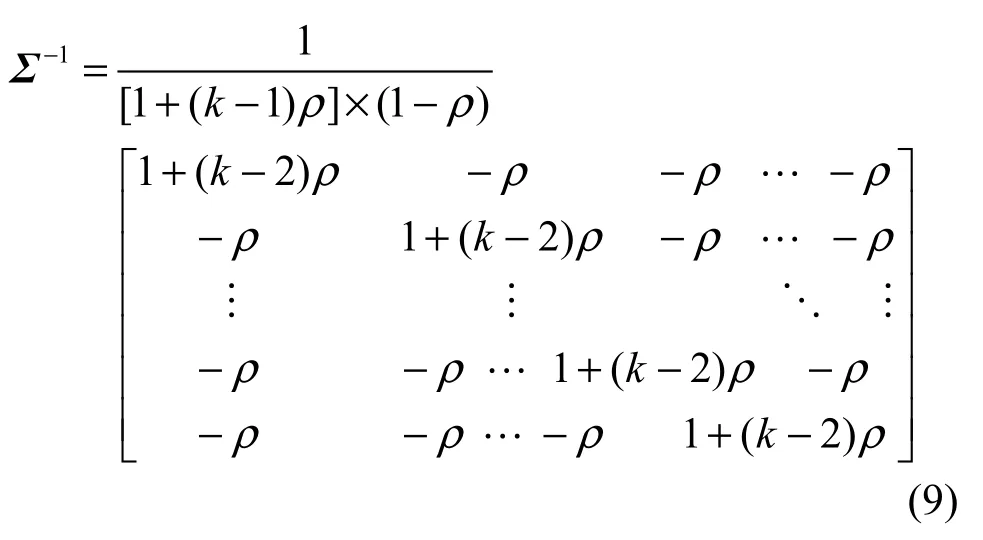
由此可得：

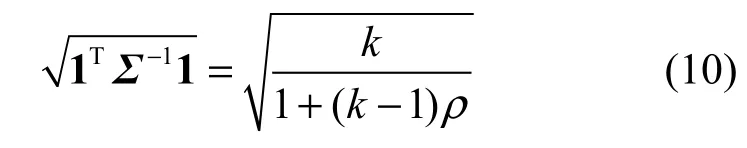
代入式（5），得到感知节点集合kω的虚警概率性能上限：

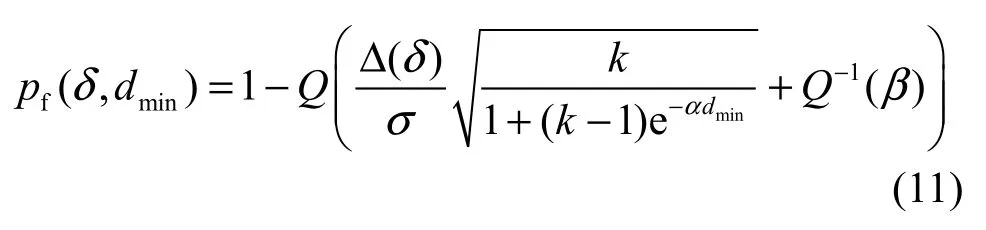
4 最优感节点集合选择

4.1 最优感知节点集合的定义

认知网络Ωn中满足系统对虚警概率和漏检概率的性能约束的感知节点集合ω一般有多个，它们之间的合作感知节点数目有可能相同，也有可能不同，因此在给定感知性能约束pm≤β和pf≤γ的条件下，从节省系统资源的角度出发，应该从这些感知节点集合中选择具有最小感知节点数目kmin的感知节点集合ω(kmin)，同样的道理，感知节点数目为kmin且满足感知性能约束的感知节点集合ω(kmin)也可能有多个。由于dmin表示感知节点集合ω(kmin)中节点间的最小距离，由式（11）可知，dmin越大，ω(kmin)的虚警概率上限 pf(δ,dmin)越小。因此当感知节点集合ω(kmin)有多个时，应该选取这些感知节点集合中感知节点间最小距离dmin最大的那个节点集合，因为这个感知节点集合的虚警概率上限最小。就是本文最终要寻找的感知节点集合，表示中感知节点间的最小距离。

4.2 kmin与之间的关系

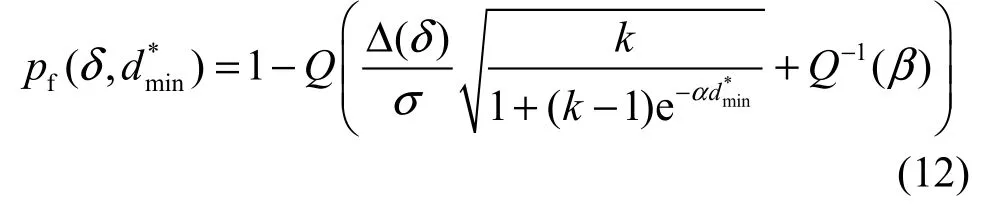
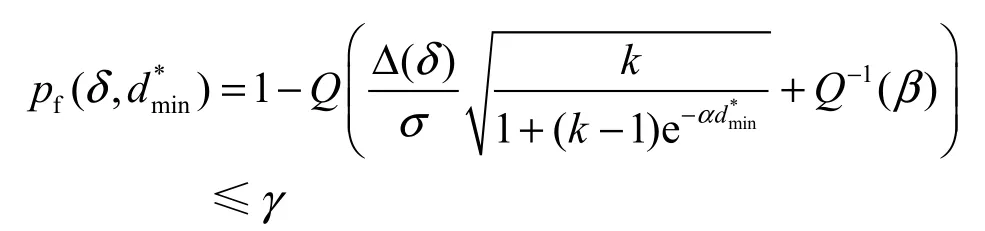
可得kmin与之间的关系表达式

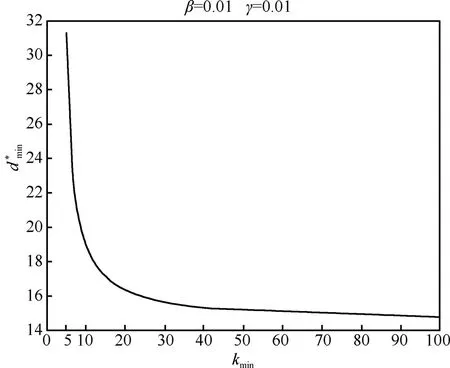
图2 kmin与之间的关系曲线

4.3 ω(kmin,)的最优选择算法

可以按照合作感知节点数目k从小到大的顺序迭代搜索满足上面 3个条件的最优感知节点集合

4.4 ω(kmin,)的贪婪选择算法

由于随着认知无线网络中认知节点的随机移动，当前最优感知节点集合 ω(kmin,)的感知性能可能不再满足系统对虚警概率和漏检概率的性能约束，因此需要重新选择一个新的最优感知节点集合来进行合作频谱感知。本文通过监测当前最优感知节点集合 ω(kmin,)的节点间最小距离的方式来判断系统是否需要重新进行选择最优感知节点集合。当＜d时，认知无线网络重新选择一个新的最优感知节点集合。

在实际应用中，如果按照式（13）的标准选择最优感知节点集合的话，由于认知节点的随机移动而导致的最优感知节点集合的更换频率将会非常大，使系统的额外资源消耗增大，因此在式（13）的基础上增加一个保护距离Δd来降低最优感知节点集合的更换频率，由此式（13）可改写为

从第 5节的仿真结果可知，Δd的大小影响着最优感知节点集合的存在概率和最优感知节点集合的失效频率，当Δd增大时，由于在选择最优感知节点集合时加入的保护距离增大，使选择出来的最优感知节点集合的失效频率降低，最优感知节点集合的更换频率也随之降低，但由于对的要求随着Δd增大而增大，因此认知网络中最优感知节点集合的存在概率随之降低。

基于以上分析，本文提出了基于贪婪的最优感知节点集合的自适应选择算法，该算法首先从认知网络Ωn中选择与节点间最大距离对应的 2个感知节点构成选择节点集合ωc，其他节点构成剩余节点集合ωr；然后在剩余节点集合ωr中选择一个感知节点（和ωr中其他感知节点相比，该感知节点与选择节点集合ωc中所有感知节点之间距离的最小值最大），并把该感知节点与ωc构成新的选择节点集合，当新的选择节点集合满足式（14）的要求时，该选择节点集合即为最优感知节点集合，感知节点集合选择过程结束，当不满足时，依次从ωr中选择节点加入ωc直到ωc满足式（14）的要求。算法进入跟踪状态后，当＜d时，重新选择一个新的最优感知节点集合。算法如下。

算法 1 基于贪婪的最优感知节点集合的自适应选择算法。

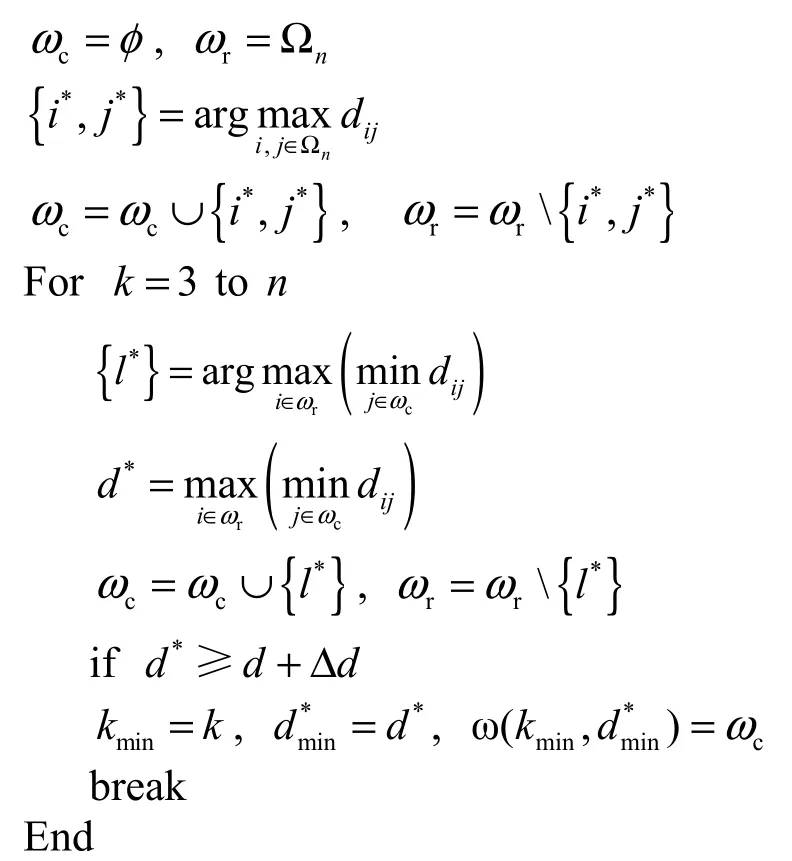
由于在每一次迭代过程中，需要从剩余节点集合rω的n-k个节点中选择一个感知节点，和rω中其他感知节点相比，该感知节点与选择节点集合cω中k个感知节点之间距离的最小值最大，而这首先需要确定rω中每一个感知节点与cω中k个感知节点之间距离的最小值，因此每一次迭代过程需要的计算量(比较次数)为(n-k) k，所以该算法的最大计算量(比较次数)近似为

5 仿真分析

本节首先对感知节点集合的最优选择算法和贪婪选择算法的最大计算量(比较次数)进行比较，比较结果如表1所示。

表1 最优和贪婪算法的最大计算量比较

从表中可以看出感知节点集合的贪婪选择算法的计算量相比最优选择算法有了明显的减少。

接下来对感知节点集合的贪婪选择算法的性能进行仿真分析，仿真中的参数设定为 β=0.01，γ=0.01，σ=2.3， Δ(δ)=-5.19，α=0.1[13]。由于在仿真时认知网络中的节点分布都是随机产生的，因此下面的仿真结果都是采用随机产生10 000次网络分布进行仿真并求平均的方法得到的[18]。在仿真中，当整个认知网络作为合作感知节点集合也不能满足性能指标时，从保证性能约束出发，选择整个认知网络作为最终要选择的感知节点集合。

图3是认知无线网络的节点数目n分别为25和 50时，最优感知节点集合的最优选择算法和贪婪选择算法所选择的最优感知节点集合的节点数目kmin随认知网络覆盖范围L增加而变化的曲线，从图中可以看出，随着L的增加，最优感知节点集合ω(kmin,)的节点数目kmin越来越小，这是由于随着L的增加，感知节点之间的相关性越来越小的缘故。图 4是认知无线网络的覆盖范围 L分别为60m和70m时，最优感知节点集合的最优选择算法和贪婪选择算法所选择的最优感知节点集合的节点数目kmin随认知无线网络节点数目n增加而变化的曲线，从图中可以看出，随着n的增加，kmin越来越小，这是因为随着n的增加，以较少节点数目满足感知性能约束的感知节点集合的存在概率提高的缘故。

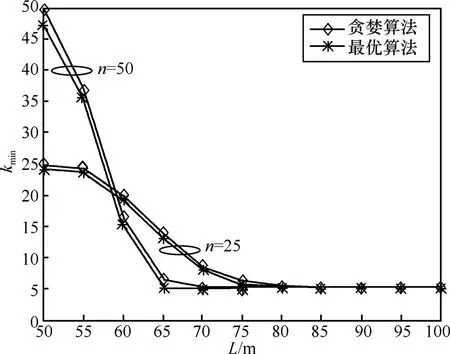
图3 认知网络节点数目固定且Δd=0时，2种算法选择的最优感知节点集合的节点数目比较

从表1与图3和图4的仿真结果可以看出，最优感知节点集合的最优选择算法和贪婪选择算法所选择的最优感知节点集合的节点数目的差别很小，但是贪婪选择算法的计算复杂度相比最优选择算法来说是大大降低了，因此贪婪选择算法相比最优选择算法更具实用性。

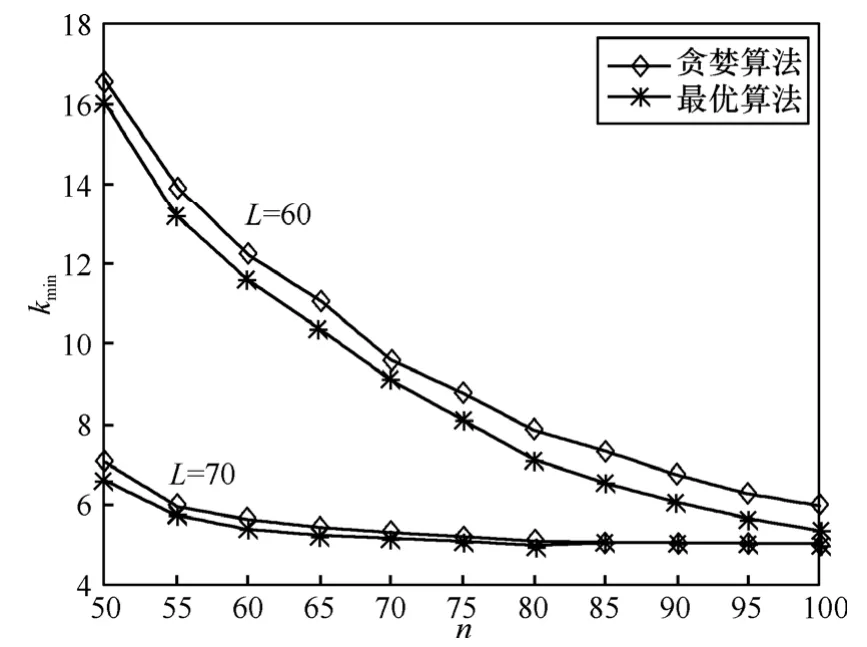
图4 认知网络覆盖范围固定Δd=0时，2种算法选择的最优感知节点集合的节点数目比较

如图5所示是本文所提出的基于贪婪的最优感知节点集合选择算法与文献[15,16]所提出的基于半径消除的感知节点集合选择算法所选择的感知节点集合的节点数目kmin随认知无线网络节点数目 n增加而变化的曲线。在仿真中参数设定L=60m，另外不考虑保护距离Δd，即Δd=0。从图 5可以看出，本文提出的基于贪婪的最优感知节点集合选择算法所选择的感知节点集合的节点数目kmin明显小于文献[15,16]所提出的基于半径消除的感知节点集合选择算法，这是由于本文提出的基于贪婪的最优感知节点集合选择算法所选择的感知节点集合能够保证它的感知节点之间具有最小的相关性，进而也就能够保证该感知节点集合在满足系统感知性能约束的条件下具有最小的感知节点数目。

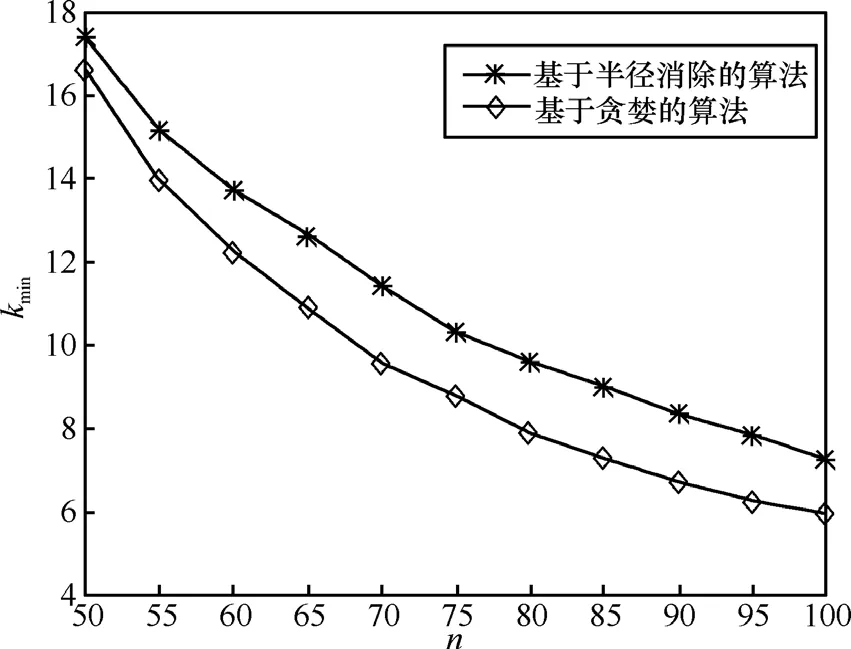
图5 基于贪婪的选择算法与基于半径消除的选择算法的系统资源消耗率比较

当认知网络覆盖范围L较小，认知网络节点数目 n较少以及保护距离Δd较大时，认知网络中不存在满足感知性能约束的最优感知节点集合，因此最优感知节点集合的存在概率是L、n和Δd的函数。图6给出了它们之间的关系曲线。从图6可以看出，最优感知节点集合的存在概率随着L和n的增大而增大，这是因为随着L的增加，感知节点之间的相关性越来越小，而随着n的增加，以较少节点数目满足感知性能约束的感知节点集合的存在概率提高的缘故。从图中还可以看出最优感知节点集合的存在概率随着Δd的增大而减小，这是因为对的要求随着Δd增大而增大的缘故。

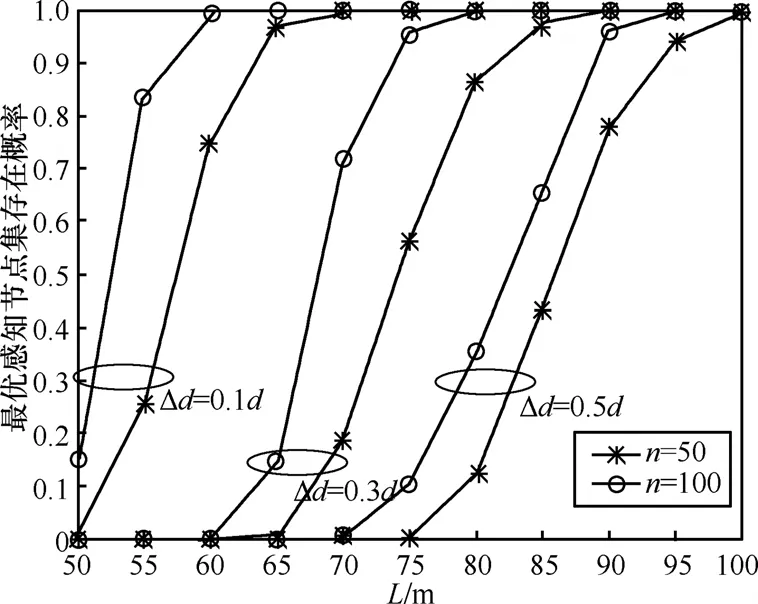
图6 最优感知节点集合在认知无线网络中的存在概率

失效频率是感知节点移动速度v与保护间隔Δd 的函数，图 7给出了它们之间的关系曲线。在仿真中采用一种现在广泛使用的PWRMM（random walk with reflection mobility model）随机移动模型对认知节点的随机移动行为进行建模[20]。采用PWRMM模型每隔1s就给每一个认知节点随机分配一个移动方向，各认知节点在这1s内使用相同的移动速度按照各自的移动方向移动，每1ms时间就判断一次当前最优感知节点集合是否失效，总仿真时间为10 000s，仿真时 L=200m，n=50。从图7可以看出失效频率随着感知节点移动速度v的提高而增加，这是必然的，这是因为随着感知节点移动速度的增加，感知节点之间的相对移动速度也相应增加，感知节点之间距离的变化速度也相应加快。从图7还可以看出失效频率随着保护间隔Δd的增加而降低，这是由于随着Δd的增大，选择出来的最优感知节点集合的最小节点间距离也相应增大的缘故。从图7可知本文所提的算法在感知节点移动速度较低时是具有一定的应用前景的。

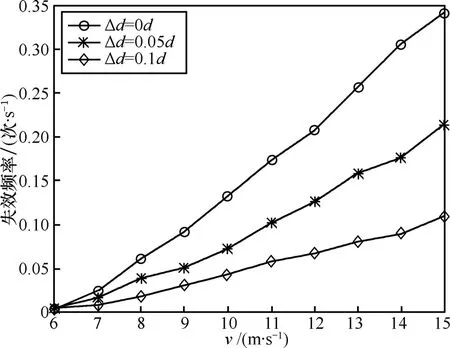
图7 最优感知节点集合的失效频率在不同保护间隔条件下随节点移动速度变化而变化的曲线

6 结束语

本文力求在感知性能与系统资源使用效率之间进行折中，提出了一种基于贪婪的最优感知节点集合的自适应选择算法。数学推导与仿真测试结果表明该算法可以在满足系统对虚警概率和漏检概率的性能约束的条件下用最少的感知节点来进行合作感知，从而使感知过程中的系统资源消耗最小化，提高了资源使用效率，同时它还可以适应由于认知节点的随机移动而引起的认知无线网络的动态拓扑变化，因此具有一定的可行性。

[1] MITOLA J,MAGUIRE G Q.Cognitive radio: making software radios more personal[J].IEEE Pers Commun,1999,6(4):13-18.

[2] HAYKIN S.Cognitive radio: brain-empowered wireless communications[J].IEEE J Select Areas Commun,2005,23(2): 201-220.

[3] LIANG Y C.Cognitive radio: theory and application[J].IEEE J Select Areas Commun,2008,26(1): 1-4.

[4] QUAN Z,CUI S G,SAYED A H.Optimal linear cooperative for spectrum sensing in cognitive radio networks[J].IEEE J Select Topics Signal Processing,2008,2(1): 28-40.

[5] STEVENSON C R,CHOUINALD G,LEI Z,et al.IEEE 802.22: the first cognitive radio wireless regional area network standard[J].IEEE Communications Magazine,2009,47(1): 130-138.

[6] SAHAI A,HOVEN N,TANDRA R.Some fundamental limits on cognitive radio[A].42nd Allerton Conference on Communications,Control and Computing[C].Monticello,IL,2004.131-136.

[7] CABRIC D,MISHRA S M,BRODERSEN R.Implementation issue in spectrum sensing for cognitive radios[A].38th Asilomar Conf Signals,Systerms and Computers[C].Pacific Grove,CA,2004.772-776.

[8] LIANG Y C,ZENG Y H.Sensing-throughput tradeoff for cognitive radio networks[A].IEEE ICC Proceedings[C].Scotland,2007.5330-5335.

[9] GHASEMI A,SOUSA E.Collaborative spectrum sensing for opportunistic access in fading environments[A].IEEE Symp New Frontiers in Dynamic Spectrum Access Networks(DySPAN)[C].Baltimore,MD,2005.131-136.

[10] UNNIKRISHNAN J,VEERAVALLI V V.Cooperative sensing for primary detection in cognitive radio[J].IEEE J Select Topics Signal Processing,2008,2(1): 18-27.

[11] QUAN Z,CUI S G,SAYED A H.An optimal strategy for cooperative spectrum sensing radio networks[A].IEEE GLOBECOM[C].Washington,DC,2007.2947-2951.

[12] UCHIYAMA H,UMEBAYASHI K,FUJII T,et al.Study on soft decision based cooperative sensing for cognitive radio networks[J].IEICE Trans Commun,2008,E91-B(1): 85-94.

[13] GHASEMI A,SOUSA E S.Asymptotic performance of collaborative spectrum sensing under correlated Log-normal shadowing[J].IEEE Communications Letters,2007,11(1): 34-36.

[14] VISOTSKY E,KUFFNER S,PETERSON R.On collaborative detection of TV transmissions in support of dynamic spectrum sharing[A].IEEE Symp New Frontiers in Dynamic Spectrum Access Networks(DySPAN)[C].Baltimore,2005.338-345.

[15] MATSUI M,SHIBA H,AKABANE K,et al.A cooperative sensing technique with weighting based on distance between radio stations[A].Asia-Pacific Conference on Communications[C].Tokyo,2008.1-4.

[16] MATSUI M,SHIBA H,AKABANE K,et al.A novel cooperative sensing technique for cognitive radio[A].International Symposium on Personal,Indoor and Mobile Radio Communications(PIMRC2007)[C].Athens,Greece,2007.1-5.

[17] KIM H,SHIN K G.In-band spectrum sensing in cognitive radio networks: energy detection or feature detection[A].14th Mobile Computing and Networking(Mobicom)[C].San Francisco,2008.14-25.

[18] VURAN M C,AKYILDIZ I F.Spatial correlation-based collaborative medium access control in wireless sensor networks[J].IEEE Transactions on Networking,2006,14(2): 316-329.

[19] BRUCKNER M.The p-center machine[A].IEEE IJCNN Proceedings[C].Canada,2005.1000-1005.

[20] HANZO L,MOSTAFAVI S M,TAFAZOLLI R.Connectivity-related properties of mobile nodes obeying the random walk and random waypoint mobility models[A].Vehicular Technology Conference[C].Singapore,2008.133-137.