基于最大比合并的超定盲源分离

姚俊良，杨小牛，李建东，付卫红，李钊，张琰

(1.西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071；2.中国电子科技集团公司 第三十六研究所，浙江 嘉兴 314001)

1 引言

在源信号和信道状态都未知的情况下，仅利用接收的混合信号来获得源信号的技术，称为盲源分离(BSS,blind source separation)[1]。近年来，BSS已成功应用到通信信号处理、语音的识别和增强、图像处理以及脑电信号处理等诸多领域[2～6]。

现有的盲源分离算法通常都假定接收天线个数等于源信号个数，即适定的盲源分离问题。但在许多实际的应用中，源信号个数并不等于接收天线个数（非适定盲源分离包括超定和欠定2种情况）。在这种情况下，混合矩阵不再是方阵，并且不再可逆，因此非适定情况下盲源分离算法的研究有更大的实际意义。而对于欠定盲源分离，如果没有源信号的额外先验信息，即使获得混合矩阵也无法分离出源信号，因此本文的讨论仅限于超定的情况。

对于超定盲源分离的研究，目前主要有2大类算法：第1类算法中，Amari、Zhang等人从李群(Lie group)和Stiefel流形出发[7,8]，将适定自然梯度算法推广到超定情况。这类基于梯度的算法收敛速度较慢，算法稳定性受混合矩阵的影响很大[9]。第2类算法首先通过白化预处理[10,11]将超定分离问题转化为适定分离，然后再利用传统的适定盲分离算法，这类算法的缺点是没有充分利用接收端的天线来获得分集增益。

在移动通信中，通常采用分集接收、合并处理的方法来获得分集增益，从而抵抗信道衰落[12]。最大比合并(MRC,maximum ratio combining)是一种较好的合并处理方式，它可以最大化接收信号的信噪比(SNR)，但MRC并没有考虑到干扰信号。FastICA算法[10]是目前常用的复信号BSS算法之一，它可以消除期望信号中的多用户干扰，但是算法并不能很好地处理噪声。

2 信号模型和FastICA算法介绍

2.1 信号模型和假设

FastICA算法是基于独立分量分析(ICA)的一种盲源分离算法，瞬时线性ICA模型可以表示为

其中，x=(x1,x2,…,xm)T、s=(s1,s2,…,sd)T和 n=(n1,n2,…,nm)T分别表示m×1维的观测信号向量、d×1维的非高斯源信号向量和m×1维的加性高斯噪声向量，A表示m×d维的混合矩阵。m、d是接收天线数目和源信号数目(本文主要研究m＞d的情况)，上标T表示转置，高斯白噪声n与源信号s的各个分量统计独立并且方差为2σ。在本文的信号模型中源信号s、混合矩阵A和噪声信号n都是复信号。

ICA的基本假设是各个源信号分量相互统计独立并且非高斯，混合矩阵A列满秩。ICA的目的是在A未知的情况下，通过寻找一个线性变换使得线性变换输出信号y的各个分量尽可能统计独立，则y就是源信号s的估计信号。下面介绍一种目前常用的解决ICA问题的算法——FastICA。

2.2 FastICA算法介绍

复信号的 FastICA算法最早由 E.Bingham[10]提出，它有串行算法(S-FastICA,serial FastICA)和并行算法(P-FastICA,parallel FastICA) 2种实现方式，它们都需要对观测信号进行白化预处理。白化处理过程如下：

S-FastICA算法的输出可表示为

其中，wi(i=1,2,…,d)表示分离矩阵W的第i个列向量，上标H表示共轭转置，yi是第i个分离信号，S-FastICA算法的核心迭代步骤如下：

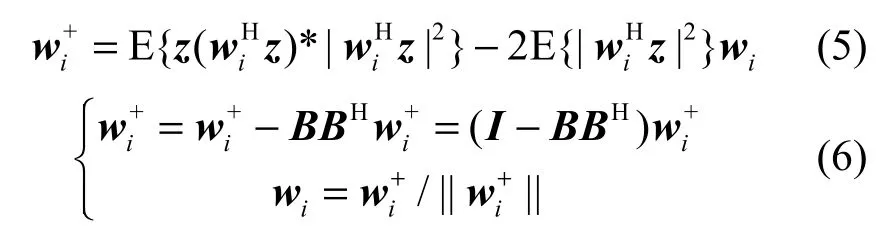
式(5)中上标*表示复数共轭，E[·]表示数学期望。式(6)中B是由已经获得的分离向量wj(j=1,2,…,i-1)组成的矩阵，当计算w1时，B取元素全为0的m 维列向量 0m×1，式(6)的目的是使 wi与已分离向量wj(j=1,2,…,i-1)相互正交，以保证算法每次分离出不同的信号分量。

并行算法 P-FastICA每次对所有分离向量W=(w1,w2,…,wd)进行迭代，为了保证分离出不同信号分量，算法在每次迭代后要进行对称正交化，这个正交化可以采用下面公式：

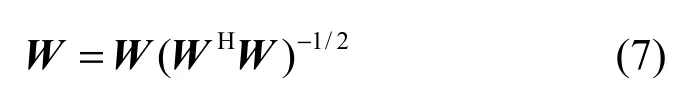
在超定情况下(m＞d)，FastICA算法通过白化可以降低信号维数和噪声，提高算法的分离性能。然而传统的FastICA算法没有充分利用接收天线的信息来获得分集增益，并且为了保证每次分离出不同的源信号，串行算法采用的压缩影射(deflation) 会引入误差累积，使得源信号恢复质量逐渐恶化。并行算法采用的对称正交化会增大分离信号中的残留干扰，导致算法性能下降。

3 MRC-FastICA算法

3.1 算法具体过程

针对传统FastICA算法存在的上述问题，本文提出一种基于最大比合并的 FastICA算法(MRC-FastICA)。算法的基本结构如图 1所示，包括下面4个实现步骤。

1) 观测信号分组

天线的接收信号为x=[x1,x2,…,xm]，分组的目的是将x分为k组：{x1,x2,…,xk}，其中xi(i=1,2,…,k)是由d个天线阵元的接收信号组成的向量。为了保证xi的混合矩阵列满秩，并且算法可以获得尽可能多的分集增益，分组需要遵循以下3个原则：①每个分组信号xi不能包含多个相同天线阵元接收的信号，因此k的理论最大值为；②这 k个分组信号包含了所有天线接收的信号，即x=x1∪x2∪…∪xk； ③不同分组信号xi、xj(i≠j)包含的分量尽可能不完全相同。

2) 源分离

d维观测向量xi的每个分量都是由d个源信号混合而成，因此对xi可以利用适定BSS算法进行信号分离。本文中BSS算法采用S-FastICA，对所有i=1,2,…,k对应的xi进行分离后，可以得到k组源信号的估计

3) 分离信号归类

这一步完成对k组估计信号的归类：将属于同一源信号的估计信号归为一类。由于FastICA算法存在顺序不确定性，因此不能简单地根据分离次序来归类信号。考虑到源信号之间相互独立，本文利用相关性作为信号归类的依据。

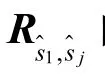
用向量 yl(l=1,2,…,d)来存储与1,l有相同源信号的估计信号，其初始值如果

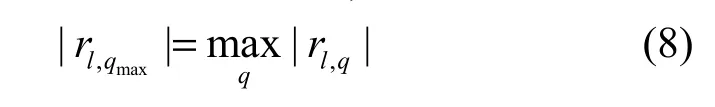
4) 最大比合并

如果在步骤3)得到的yl是第j个源信号的估计，则有如下信号模型：

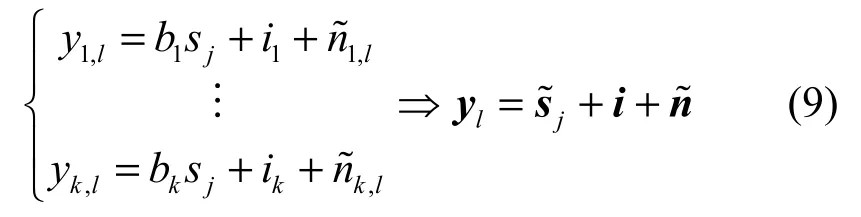
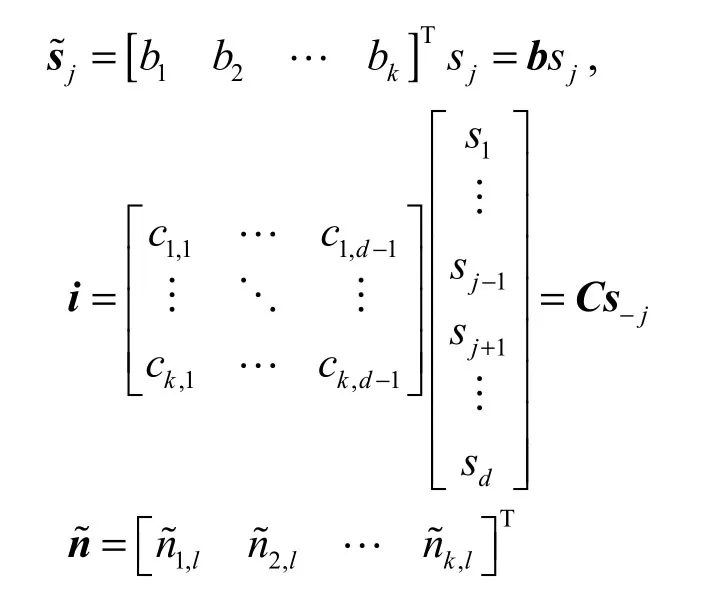
其中，s-j表示源信号s中除了sj的剩余信号组成的信号向量，b、C 为未知的 k×1、k×(d-1)维系数矩阵。最大比合并的目的就是寻找一个合并向量vl，使得合并输出的信号ˆl（即源信号sj的最终估计值）信干噪比（SINR）最大。合并输出信号为的SINRl为

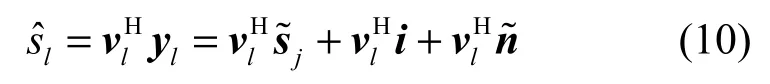
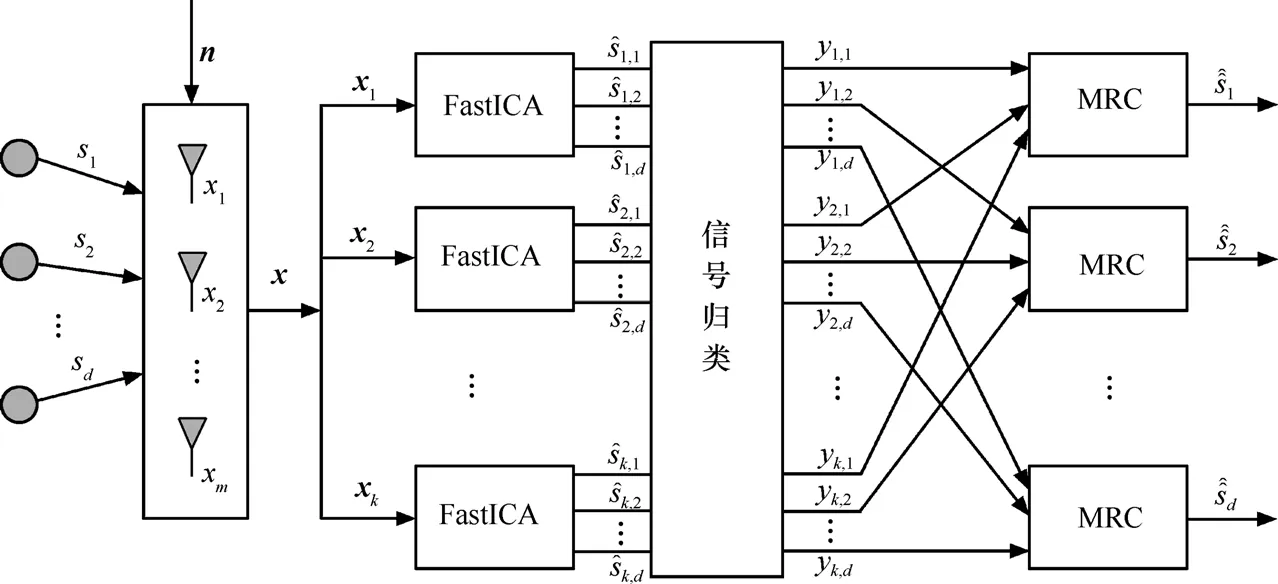
图1 MRC-FastICA算法结构

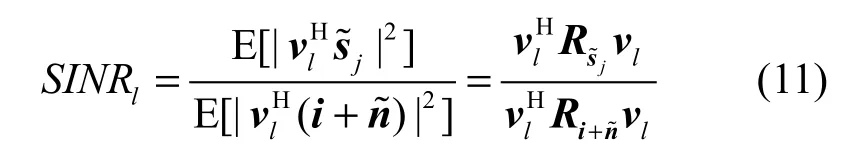
式(11)是标准的广义Rayleigh商形式，从文献[13]可知，使其最大化的权值向量为

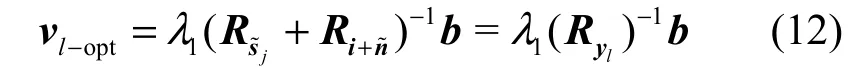
其中，Ryl=Rs˜j+Ri+n˜是第l组归类信号(式(9))的自相关矩阵，最佳系数

式(12)得到的权值向量vl-opt虽然是最佳的，但它需要知道向量b，在本文中b是无法获得的。通过分析发现，式(12)与最大化目标函数(13)所得的收敛解vl[14,15]仅相差一个常系数。

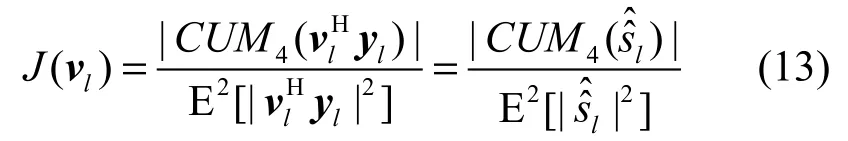
目标函数J(vl)的最大化可以采用梯度法。

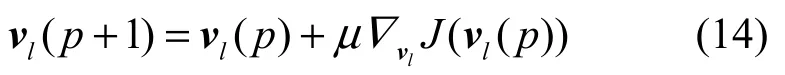
其中，µ是步长因子，p表示迭代次数，文献[14]给出式(14)中∇vlJ(vl)的表达式如下：

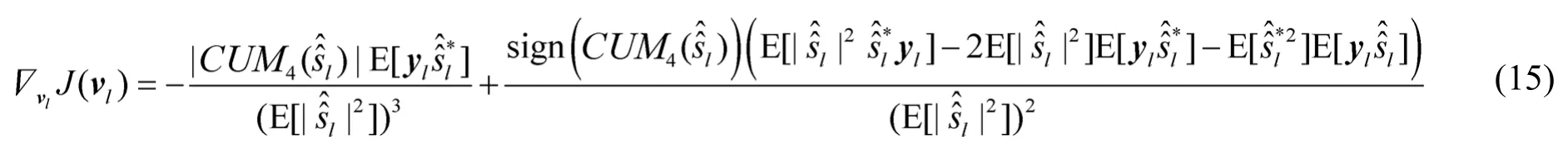
当µ值的选择合适，梯度法(14)可以保证算法收敛，但它存在收敛速度慢的缺点。为了提高收敛速度，在本文的算法中，先采用超指数算法[17]得到一个 vl的初始值，然后利用梯度法(14)迭代直至收敛。超指数算法的核心迭代公式如下：

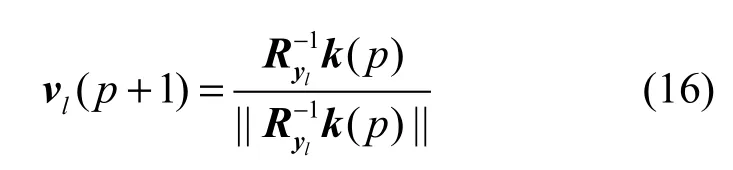
其中，

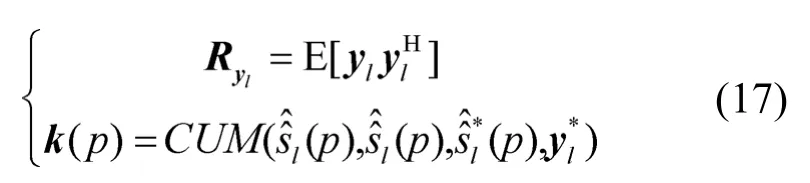
1) 令p=1，随机选取一个k维的单位模值合并向量vl(p)，可得

2) 利用式(16)对 vl(p)进行迭代，得到 vl(p+1)和(p+1)。

3) 如果(式 13)目标函数 J(vl(p+1))＞J(vl(p))，令p=p+1，返回2)继续迭代；否则令p=p+1执行4)。

4) 利用式(14)对vl(p)进行迭代，得到vl(p+1)。

5) 如果式(14)中∇vlJ(vl(p))大于设定的门限值β，则算法还没有收敛，令p=p+1，返回4)继续迭代，否则算法收敛，第l个估计信号为

3.2 算法总结

综上所述，MRC-FastICA算法执行的具体过程如下。

1) 观测信号分组：从m个天线阵元的观测信号中随机选择d个，组成d维的观测信号向量xi。重复执行k次，形成k组d维观测信号向量：{x1,x2,…,xk}。

2) 源分离：利用S-FastICA算法对xi(i=1,2,…,k)进行分离，可以得到 k组源信号的估计

4) 最大比合并：利用MRC算法对yl进行合并，得到估计信号ˆl。对l从1到d重复执行，可以得到所有源信号的估计：

下面对MRC-FastICA算法进行讨论。

1) 如果信源数 d已知，可以直接利用MRC-FastICA算法进行信号分离。而在实际的情况下，源信号个数有可能是未知的，首先需要估计 d的值。估计方法包括：子空间方法[18]和基于信息论准则的方法[19]。

2) MRC-FastICA算法的分离信号依然存在顺序模糊性，对于复信号，还存在相位模糊性，这对很多实际系统(特别是无线通信系统)的后续处理是非常不利的，这个问题可以通过利用其他先验信息设计半盲算法来解决[20]。

3.3 算法示例及定性分析

下面通过一个简单示例来描述 MRC-FastICA算法的执行过程。

例：图1中源信号数d=2、接收天线数m=3，因此观测信号向量。

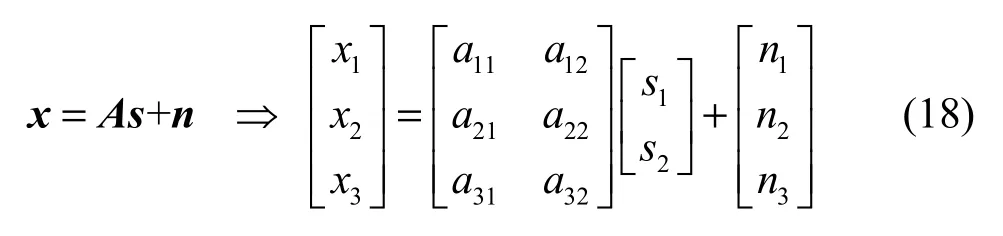
如果算法的分组数 k=2，按照分组原则，2组适定混合的观测信号向量可表示为

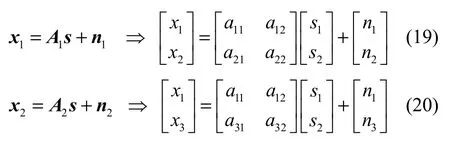
利用传统的串行S-FastICA算法对x1、x2进行适定盲源分离，得到2组源信号的估计如下(这里不考虑观测信号的预白化)：

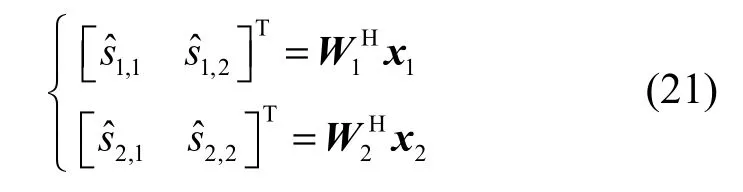
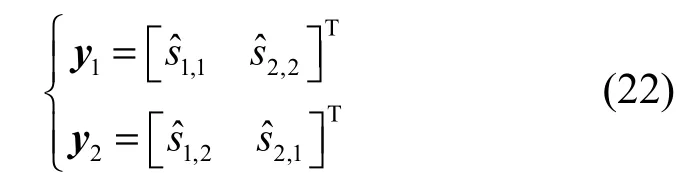
如果对式(21)的2组分离信号进行归类后得到：其中，y1和y2分别为对应于s1和s2的归类信号，对y1、y2分别进行最大比合并，可得到源信号的最终估计值：

定性分析：从式(22)可以看出，属于源信号 s1的 2个估计信号为1,1和2,2，这 2个信号有不同的SINR性能，这主要是以下2个原因造成的：①1,1和2,2分别属于观测信号x1和x2的分离信号，而x1、x2的混合系数 A1和 A2不同将会使1,1和2,2的 SINR性能不同；② 从式(21)可知，1,1是 x1的第 1个分离信号，2,2是x2的第 2个分离信号(S-FastICA算法存在顺序模糊性)，而由于S-FastICA算法存在误差累积，不同的分离次序会导致不同的分离性能，因此1,1和2,2的 SINR 性能不同。

从上面的讨论可知，MRC-FastICA算法是对具有不同SINR性能的多个分离信号(对应于同一源信号)进行最大比合并，来得到最终的分离信号。移动通信中经常采用多条具有独立衰落特性的路径来传输相同的信息，并在接收端对接收到的信号进行适当合并来获得分集增益，从而抵抗信道衰落。同样本文算法通过对多个具有不同SINR性能的分离信号进行最大比合并，也可以获得分集增益。

4 仿真实验和结果分析

实验中源信号个数d=4，并且4个独立源信号为同频数字调制信号，分别为2个16PSK信号，2个QPSK信号。接收端是m阵元的等距线阵，因此混合矩阵的第i个列向量为

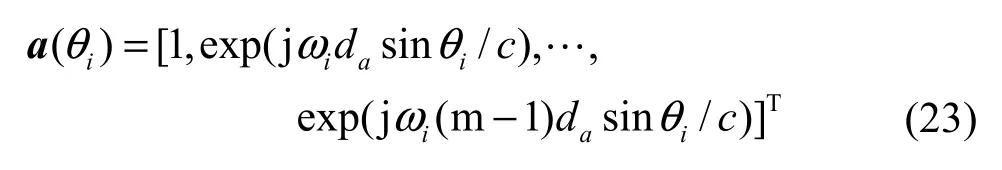
其中，da表示等距线阵相邻天线之间距离，它的值取为信号波长的一半，c是光速，ωi、θi分别是第i个信源的角频率和入射角度，θi在[0,π]内服从均匀分布，MRC算法中的门限值β=10-4，式(14)的步长因子µ=1，算法采用的样本数为1 000。

实验1 在m=8和SNR=20dB时，仿真了4种算法的分离效果，这4种算法分别是S-FastICA算法[10]、P-FastICA 算法[10]、基于相对梯度的 EASI算法[11]和本文提出的MRC-FastICA算法。图2是一次实验的仿真结果，分别画出了源信号、混合信号以及4种算法得到的分离信号的星座图。

在本次实验中，源信号入射角 θ=[θ1,θ2,θ3,θ4]和混合矩阵 A=[a(θ1);a(θ2);a(θ3);a(θ4)]分别为：

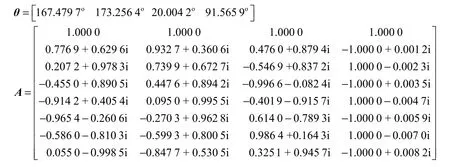
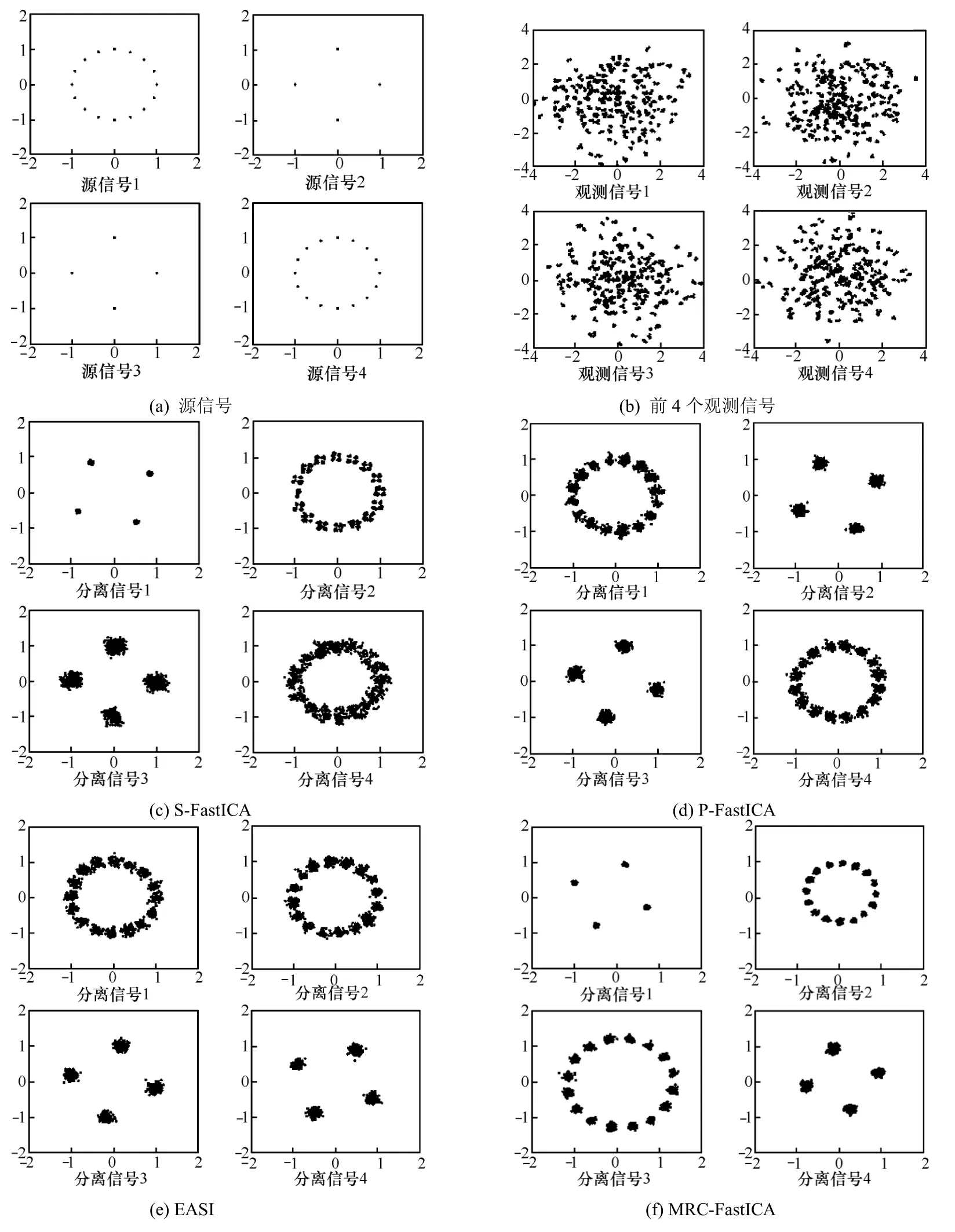
图2 源信号、分离信号以及4种算法得到的分离信号星座图

图 2(c)是 S-FastICA算法的分离信号星座图，从中可以看出，算法存在误差累积，分离的信号质量越来越差；图2(d)、图2(e)分别给出了P-FastICA和 EASI算法的分离信号星座图，可以看出P-FastICA和EASI算法的性能基本相同，这2种算法在每次迭代中都对分离矩阵进行了正交化处理(前者是对每次迭代得到的分离矩阵进行对称正交化，后者是在算法中加入了正交化约束)，这个正交化处理会增大分离信号中的残留干扰，导致算法分离性能下降；图2(f)是MRC-FastICA的分组数k=4时的分离结果，从图中可以看出其分离性能最好，这是因为当k=4时，MRC-FastICA算法可以充分利用接收天线的信息来获得分集增益，降低了串行算法误差累积的影响。与并行算法相比，本文算法避免了正交化处理带来的互干扰，因此它的分离效果最好。上述4种算法都存在顺序模糊性问题，因此分离信号与源信号之间的对应关系不完全一致，这可以通过设计半盲算法来解决。

实验2 从第3节中算法的分析过程可知，对多组分离信号的正确归类是最大比合并的基础，本文利用信号的相关性来进行信号归类，并仿真了在不同 SNR情况下，算法正确归类概率随样本数的变化。实验中衡量归类正确的方法是：如果归类信号中所有分量两两之间都满足步骤 3)所提出的归类原则(相关函数模值矩阵中对应元素最大)，并且在每次归类结束后，所有分离信号都被归到某一类中，则认为本次归类正确。

图3给出了m=8时的仿真曲线，仿真中MRCFastICA算法分组数k=4，仿真结果是1 000次独立仿真后统计得到的。从图3可以看出，随着SNR和样本数的增加，算法正确归类的概率也呈增大趋势。当SNR=10dB，正确归类概率在样本数大于400时基本保持在0.9左右。当SNR=20dB时，正确归类概率在样本数大于200时保持稳定，达到0.96左右。

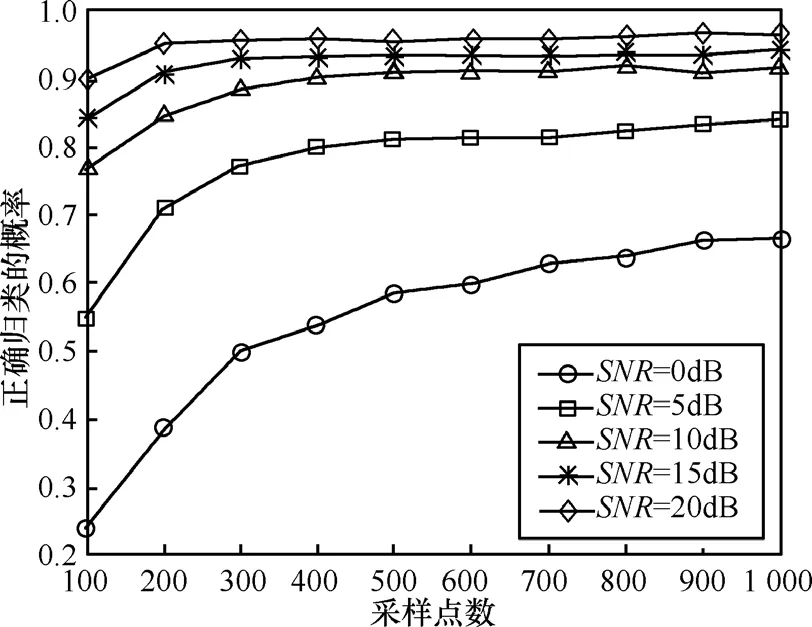
图3 分离信号正确归类概率与样本数之间的关系

实验 3 本实验仿真了分离信号的输出 SINR(signal-to-interference- plus-noise ratio)性能，仿真结果是500次独立仿真后进行平均得到的。下面给出仿真中分离信号SINR的表达式。

若第i个分离信号的最终分离向量为fi，，则第i个分离信号为

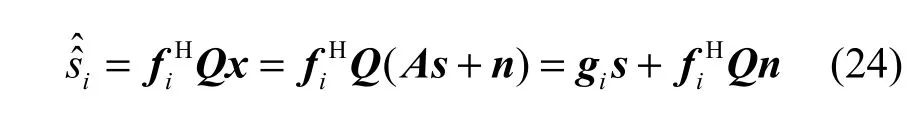
它的SINR可以表示为

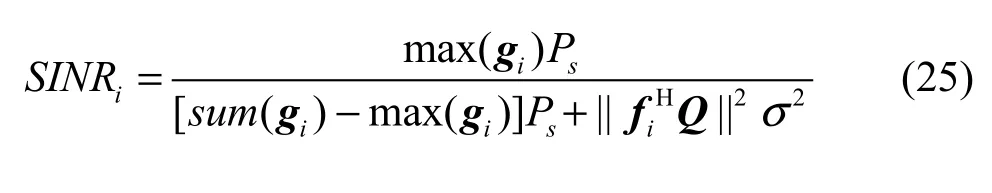
其中，Ps为源信号功率，max(gi)是向量gi的最大元素、sum(gi)是向量gi所有元素之和。分母第1项、第2项分别表示分离信号中干扰分量和噪声分量的功率。

图4给出了当m=8，SNR=20dB时，4种算法分离信号SINR随分离信号次序变化的曲线。其中MRC-FastICA算法的分离信号次序是按照 x1的分离次序来排列的，算法的分组数 k=4。从图中可以看出，S-FastICA算法由于误差累积的影响，分离性能随着分离次序的增大逐渐下降，图中S-FastICA算法第一个分离信号SINR高于输入SNR(20dB)，这是因为在本实验中，接收天线阵元数(m=8)大于信源个数(d=4)，这种情况下算法采用的预白化可以降低噪声的影响；P-FastICA算法和EASI算法由于正交化约束使得整体分离性能下降，这与实验1的结果是吻合的。MRC-FastICA算法由于获得了分集增益，因此大大降低了误差累积的影响，算法的整体性能最好。图5给出了4种算法的SINR性能随SNR的变化曲线。从图中可以看出，随着SNR的增加，4种算法的各个分离信号SINR都随SNR的增加而增大。由于可以获得分集增益，MRC-FastICA算法的性能要优于其他3种算法。

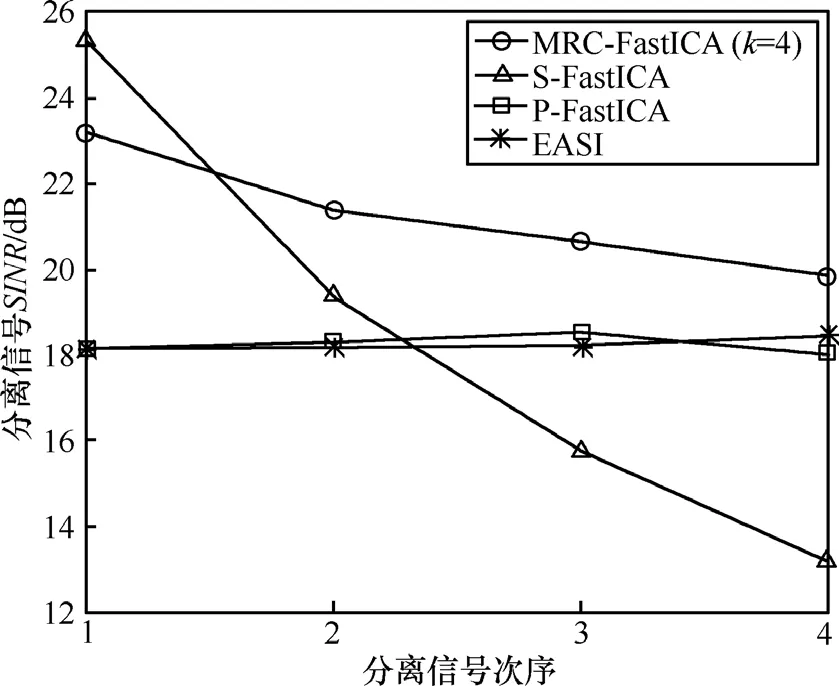
图4 分离信号SINR与分离信号次序

图6给出了分组数k取不同值时MRC-FastICA算法得到的分离信号SINR性能曲线。从图中可以看出，k值越大，MRC-FastICA算法的性能越好。这是因为k值越大，算法利用的天线组合越多，分集增益也就越大。当k=1时，算法没有利用到多余天线来提供分集，而且也没有利用多余天线来降低噪声，因此算法性能要劣于传统S-FastICA算法。

图 7所示为当接收天线数 m取不同值时，MRC-FastICA算法(k=4)得到的分离信号SINR性能曲线。从图中可以看出，m值越大，算法性能越好。这是因为接收天线数越多，算法可利用的观测信号信息越多，分集增益也就越大。

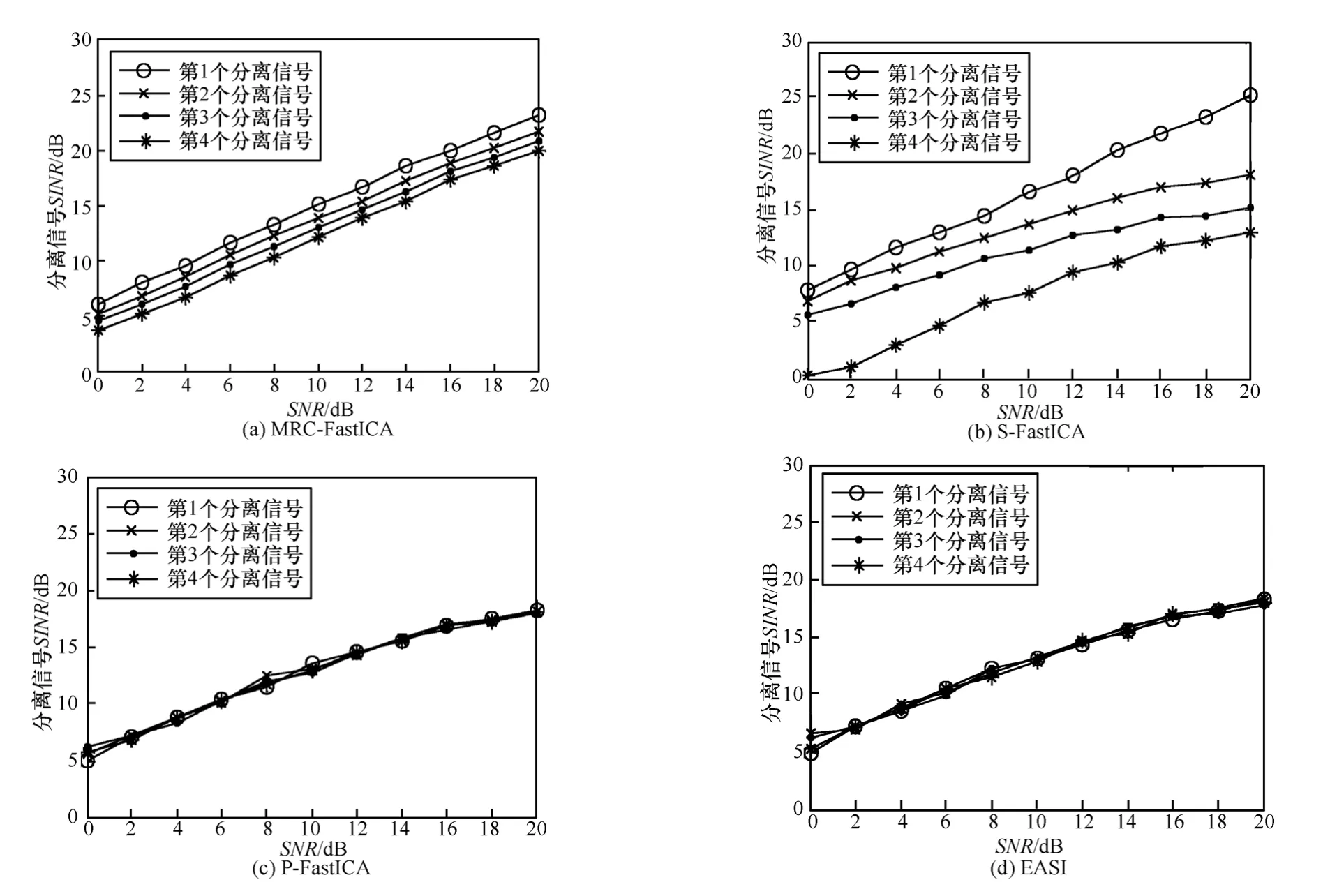
图5 分离信号SINR性能随SNR的变化曲线

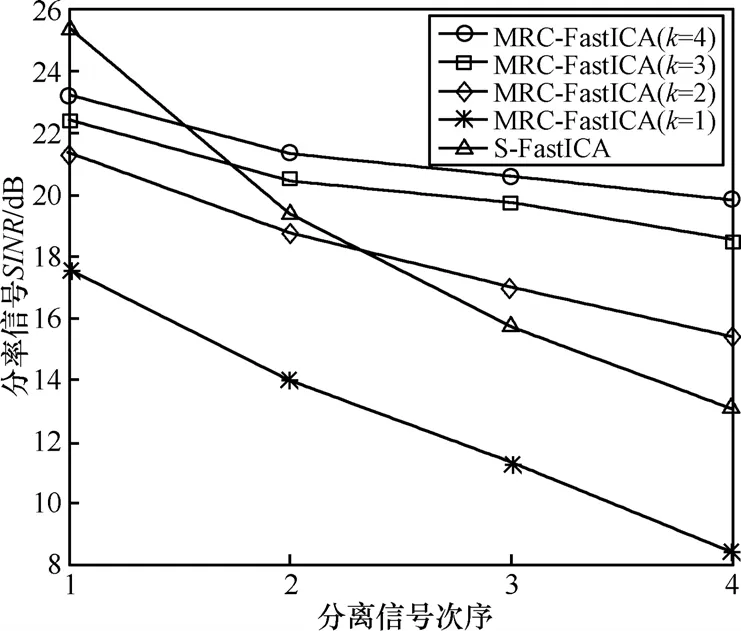
图6 分组数对MRC-FastICA算法分离性能的影响

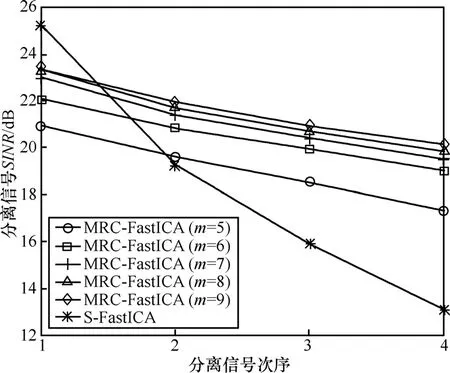
图7 接收天线数对MRC-FastICA分离性能的影响

5 结束语

本文提出一种基于最大比合并的超定盲源分离算法，该算法利用 S-FastICA来消除期望信号中其他用户的干扰，为 MRC提供同一源信号的多个分集信号，并利用 MRC得到最终的分离信号。仿真实验和分析表明，所提算法通过对不同观测信号组合的分离信号进行最大比合并，可以获得分集增益，并且随着分组数和接收天线数的增大，分集增益也增加。该分集增益不仅可以降低 S-FastICA中误差累积的影响，而且避免了串行算法由于正交化处理带来的残留干扰，算法有更好的SINR性能。

[1] CICHOCHI A,AMARI S I.Adaptive Blind Signal and Image Processing[M].New York: Wiley,2002.

[2] 付卫红,杨小牛.基于盲源分离的CDMA多用户检测与伪码估计[J].电子学报,2008,36(7): 1319-1323.FU W H,YANG X N.The multi-user detection and chip sequence estimation for CDMA system based on the blind source separation[J].Acta Electronica Sinica,2008,36(7): 1319-1323.

[3] 张晋东，秦贵和.基于FastICA-TDS的DS-CDMA盲源分离系统[J].通信学报，2008，29(8): 124-128.ZHANG J D,QIN G H.DS-CDMA BSS system based on FastICA-TDS[J].Journal on Communications,2008,29(8): 124-128.

[4] ERDOGAN A T.Globally convergent deflationary instantaneous blind source separation algorithm for digital communication signals[J].IEEE Transactions on Signal Processing,2007,55(5): 2182-2192.

[5] CHAN T H,MA W K.Blind separation of non-negative sources by convex analysis: effective method using linear programming[A].IEEE International Conference on Acoustics,Speech,and Signal Processing(ICASSP)[C].Las Vegas,Nevada,USA,2008.3493-3496.

[6] ZHANG Q,SUN J D.A novel ICA-based image/video processing method[A].7th International Conference on Independent Component Analysis and Signal Separation(ICA2007)[C].London UK,2007.836-842.

[7] AMARI S I.Natural gradient learning for over and under-complete bases in ICA[J].Neural Computation,1999,11(8): 1875-1883.

[8] ZHANG L Q,CICHOCKI A,AMARI S I.Natural gradient algorithm for blind separation of overdetermined mixture with additive noise[J].IEEE Signal Processing Letters,1999,16(11): 293-295.

[9] SQUARTINI S,ARCANGELI A.Stability analysis of natural gradient learning rules in overdetermined ICA[J].Signal Processing,2008,88(3): 761-766.

[10] BINGHAM E,HYVARINEN A.A fast fixed-point algorithm for independent component analysis of complex valued signals[J].Journal of Neural Systems,2000,10(1):1-8.

[11] CARDOSO J F,LAHELD B H.Equivariant adaptive source separation[J].IEEE Transactions on Signal Processing,1996,44(12): 3017-3030.

[12] 张辉,曹丽娜.现代通信原理与技术[M].西安: 西安电子科技大学出版社,2002.ZHANG H,CAO L N.Modern Principle and Technology of Telecommunications[M].Xi’an: Xidian University Press,2002.

[13] ZHANG X D.Matrix Analysis and Applications[M].Beijing:Tsinghua University Press,2004.

[14] DING Z,NGUYEN T.Stationary points of a kurtosis maximization algorithm for blind signal separation and antenna beamforming[J].IEEE Transactions on Signal Processing,2000,48(6): 1587-1596.

[15] CHI C Y,CHEN C Y.Blind beamforming and maximum ratio combining by kurtosis maximization for source separation in multipath[A].Proceedings of the IEEE Signal Processing Workshop on Signal Processing Advances in Wireless Communications[C].Taoyuan,Taiwan,China,2001.20-23.

[16] CHI C Y,CHEN C Y.Batch processing algorithms for blind equalization using higher-order statistic[J].IEEE Signal Processing Magazine,2003,(1): 25-49.

[17] SHALVI O,WEINSTEIN E.Super-exponential methods for blind deconvolution[J].IEEE Transactions on Information Theory,1993,39(2):504-519 .

[18] OZGUL B,DELIC H.Wireless access with blind collision-multiplicity detection and retransmission diversity for quasi-static channels[J].IEEE Transactions on Communications,2006,54(5):858-867.

[19] WAX M,KAILATH T.Detection of signals by information theoretic criteria[J].IEEE Transactions on Acoust,Speech,Signal Processing,1985,32: 387-392.

[20] ZENG Y H,NG T S.A semi-blind channel estimation method for multiuser multiantenna OFDM systems[J].IEEE Transactions on Signal Processing,2004,52(5): 1419-1429.