FMT 系统中的迭代信道估计和Turbo 均衡
钟华,郑林华
(1.国防科技大学 电子科学与工程学院,湖南 长沙 410073;2.95746部队,四川 成都 611531)
1 引言
多载波调制由于能够有效克服高速数据传输中信道造成的码间干扰而被广泛应用于新一代无线通信系统中。FMT作为一种新型的多载波调制技术,于1999年提出,用于解决VDSL中的回波噪声(ECHO)、近端串扰(NEXT)和远端串扰(FEXT)等问题[1]。FMT与OFDM的本质区别在于FMT子信道频谱不重叠。正因为如此,FMT系统的信道间干扰(ICI)很小,系统抗频偏性能好,并且不需要循环前缀和虚载波等开销。近年来,关于 FMT在无线通信中的研究也日益增多[2~4]。
FMT系统子信道频谱不重叠是通过不满足理想重构条件的原型滤波器来实现,这将不可避免地引入符号间干扰(ISI)[5],尤其当FMT应用于无线多径环境时,ISI将进一步增大,导致误码率急剧增加,严重影响FMT系统的性能。因此,在接收端必须采用均衡来消除ISI。Turbo均衡通过将信道均衡和译码联合处理,在迭代过程中,均衡器充分地利用了信道编码所带来的冗余信息,获得了很好的均衡效果[6,7]。但Turbo均衡器在计算输出软信息时需要知道信道响应[6,7],对于信道响应未知的情况,通常采取信道估计的方法来估计出信道响应。传统FMT系统信道估计方法是通过特殊的训练序列[8]或导频[9]的方法来完成,并没有充分利用软输入软输出(SISO)译码器输出的关于发送数据的软信息。而基于软信息的迭代信道估计算法已经得到了广泛研究[10,11]。基于以上分析,本文将基于软信息的迭代信道估计算法应用于FMT系统,提出了一种联合迭代信道估计和Turbo均衡的FMT系统接收方法,通过对FMT系统每个子信道的等效冲激响应进行迭代估计,然后采用基于线性滤波器结构的 Turbo均衡器来消除 ISI。仿真结果表明,不论采用 QPSK或16QAM调制方式,经过2次以上的迭代后,新算法的BER性能都优于传统的DFE均衡算法。
2 FMT系统模型
FMT是一种基于滤波器组的多载波调制技术,它是通过原型滤波器将整个信道划分为若干个频带有限且互不重叠的子信道,用多个子载波在这些子信道上进行信息的并行传输,其等效基带模型如图1所示。M路并行的调制数据An,i,i=0,1,…,M-1进行K倍(K=M时为严格采样,K>M为非严格采样)插值后经过一个低通滤波器H(f)(时域脉冲响应为h(n))进行带限,再用一组等频率间隔的子载波进行频率搬移,M路信号叠加后进入信道;在接收端,用对应的子载波从接收信号中解调出每路调制信号,经过与发端低通滤波器对应的匹配滤波器G(f)(时域脉冲响应为g(n))后,再进行K倍信号抽取,便恢复了原始的调制信号。与OFDM类似,FMT也可采用IFFT/FFT结构来实现[1]。
根据匹配滤波器的定义,g(n)与h(n)的关系式为
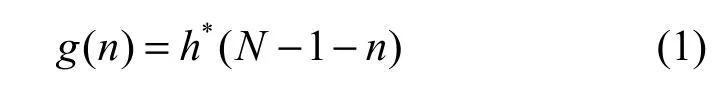
其中,“*”表示共轭运算。由于h(n)通常采用 FIR滤波器来实现,滤波器系数是实数且对称,因此,匹配滤波器即等同于原型滤波器。

3 迭代信道估计和均衡算法
FMT系统的迭代信道估计和Turbo均衡结构如图2所示。
发端二进制数据经卷积编码器编码、交织、串/并变换后产生FMT每个子信道的基带二进制数据An,i由二进制数据dn′,i根据不同的调制方式映射产生,因此,An,i对应于一个子序列,即 An,i由Q 个二进制数据dn′,i所组合成的数据决定,其中,Q=lbML(ML为调制阶数),其对应关系由比特序列集合的映射确定,而比特序列集合到符号序列集合的映射关系则由调制方式决定;接收端经 FMT解调后的信号n,i作为 SISO 均衡器的输入,每个子信道SISO均衡器输出的外信息经并/串变换和解交织后产生 SISO译码器的输入,而译码器输出经交织和串/并变换后作为SISO均衡的先验信息,从而实现迭代均衡。当迭代完成后,根据SISO译码器输出的码元LLR来判决所接收的信号(注:由于每个子信道符号持续时间为T,其时间序号为n,而编译码部分每一符号持续时间为T/K,其时间序号为k;i表示子信道序号)。
发端数据An,i的均值和方差为
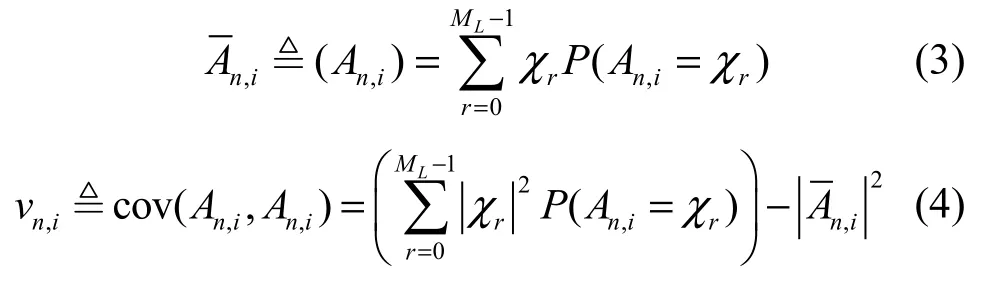
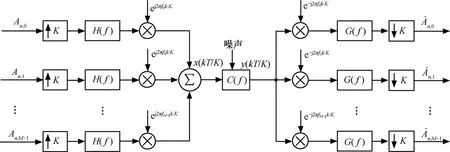
图1 FMT系统模型
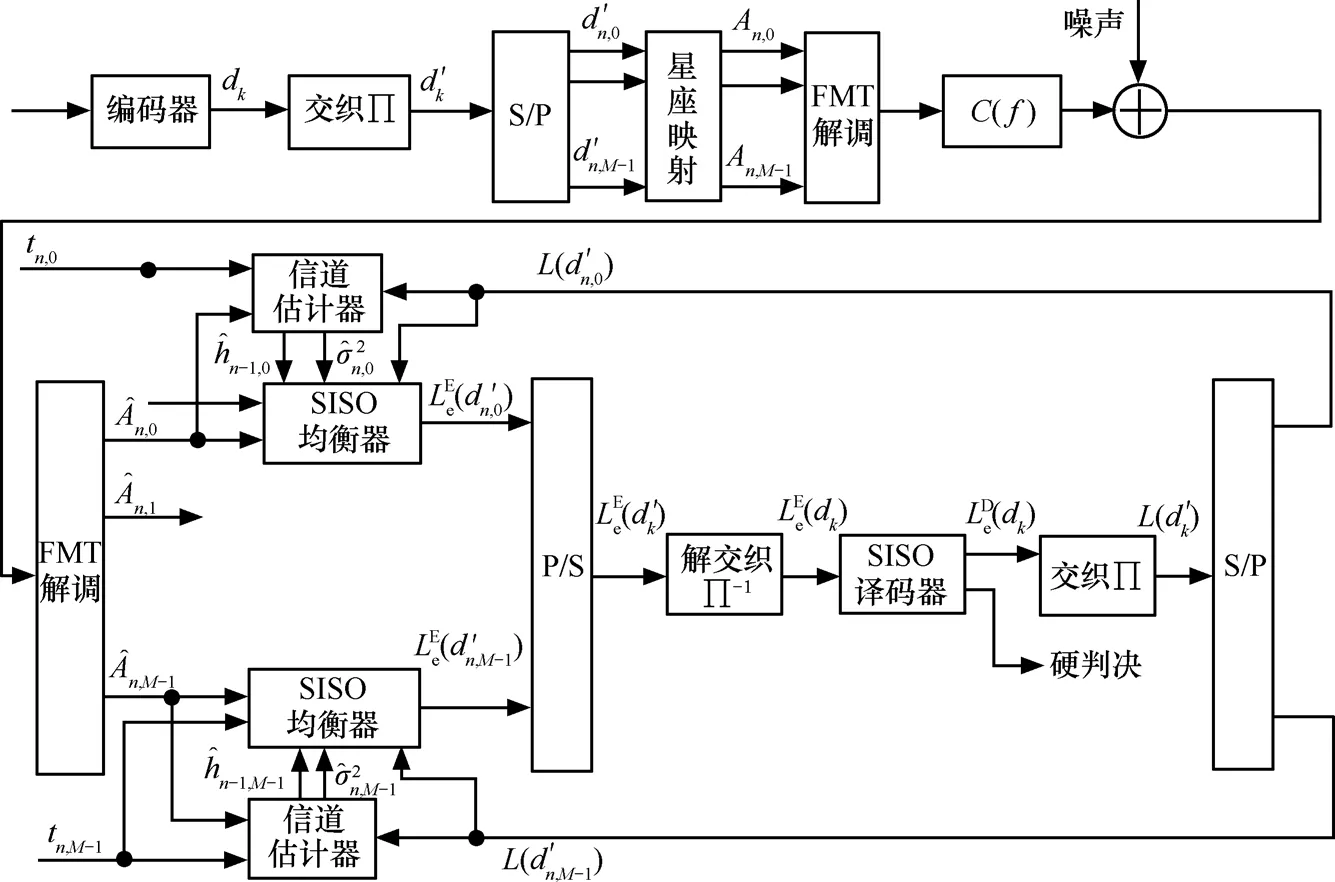
图2 FMT系统子信道Turbo迭代均衡结构
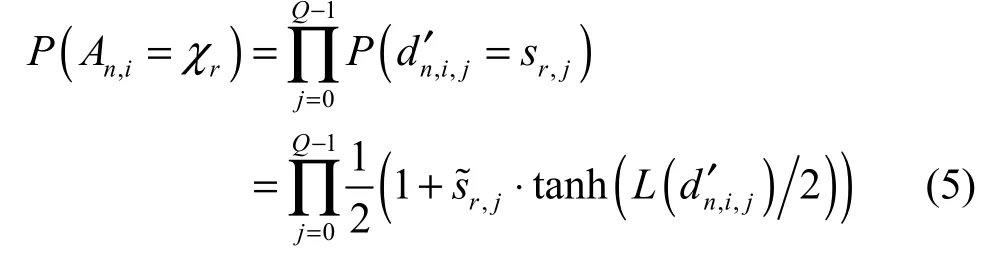
其中,
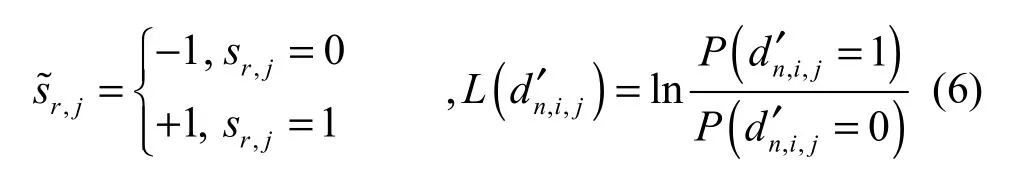
图2中信道估计器需要借助于训练序列tn,i来实现。当信道衰落特性不随时间变化时,只需在每个子信道传输数据之前发送一定长度的训练符号Trn,i(Trn,i∈S)来估计信道响应,而后续数据则按该估计值来进行处理;而当信道衰落具有时变特性时,则需要每隔一定时间间隔重复发送训练符号来估计信道的响应。以下分析假设每个子信道发送的每帧数据由长度为NTr的训练符号Trn,i和长度为NData的数据符号An,i组成。
FMT系统第i个子信道的等效冲激响应可以表示为
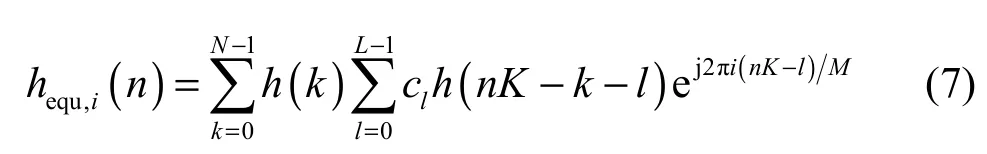
其中,cl为信道的冲激响应,经FMT解调后的信号可以表示为
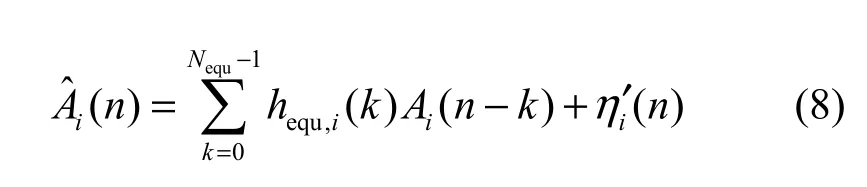
其中,Nequ为第 i个子信道等效冲激响应的长度,ηi′(n )是高斯白噪声ηi(n)经接收端分析滤波器后所产生。因此,ηi′(n )不再具有白噪声的性质。
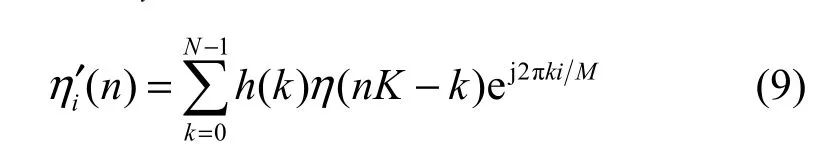
当信道响应未知时,hequ,i(n)也不能确定,本文将研究利用 SISO译码器输出的码元对数似然比(LLR)来对hequ,i(n)进行估计。令hequ,i(n)的估计值为 hˆn,i,其长度为 Ne′qu,第 i个子信道经 FMT 解调后的信号可以表示为
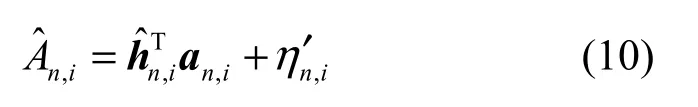
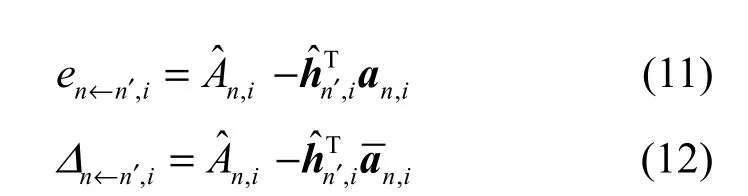
RLS估计算法所定义的代价函数为[12]
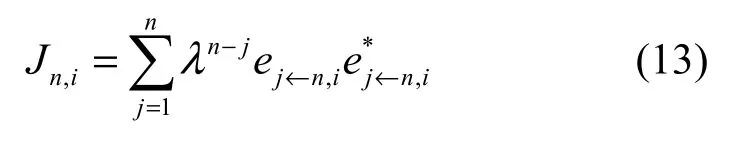
其中,λ为所加指数窗的系数。当接收端已知发送数据An,i,即发送训练数据时,hequ,i的估计值n,i为[13]
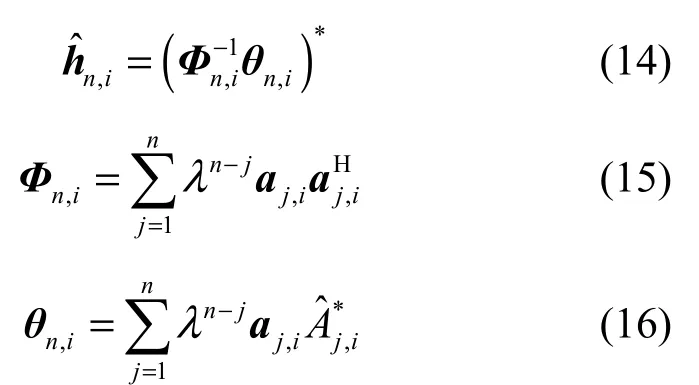
由式(15)和式(16)可知,Φn,i和θn,i可以通过递归的方式计算,即
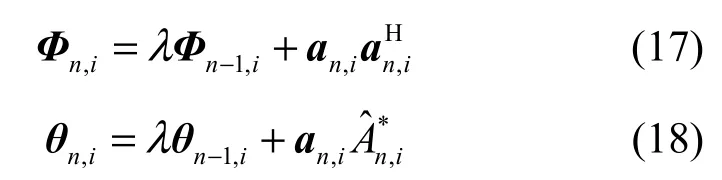
式(13)是通过 en←n′,i来定义的代价函数,而en←n′,i与SISO译码器输出无关,因此,通过式(14)来计算hequ,i(n)的估计值时无法利用SISO译码器输出的软信息。传统的基于软信息的RLS信道估计算法将式(13)中的 en←n′,i用Δn←n′,i代替,从而建立起与SISO译码器输出软信息之间的联系。但是当发送数据 An,i的方差 vn,i≠ 0时,第i个子信道实际误差为 en←n′,i而不是 Δn←n′,i。因此,传统的 RLS信道估计算法并不是最优解。
n时刻信道估计器确知的信息包括接收数据Aˆn,i,n′时刻等效信道响应的估计值 hˆn,i以及利用SISO译码器输出的软信息经式(3)和式(4)计算出的 An,i的均值和方差。本文利用这些已知量,以条件期望的形式重新定义了一种代价函数,以克服传统基于软信息的RLS信道估计算法的缺点。该代价函数为
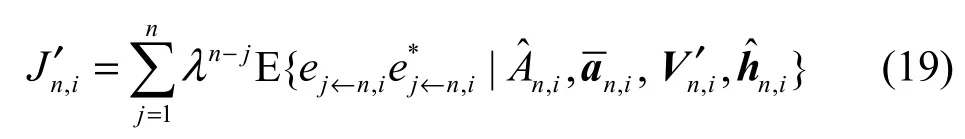
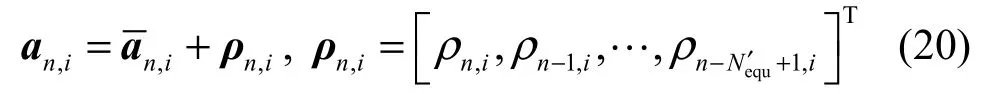
其中,ρn,i均值为零,方差cov(ρn,i,ρn,i)=Cov(An,i,An,i)=vn,i。因此,发送数据 An,i的自相关矩阵Dn,i可以表示为
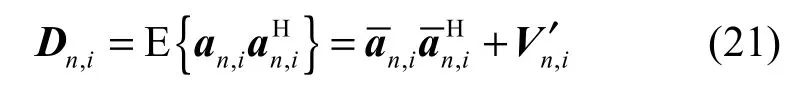
将式(11)和式(21)代入式(19),可得
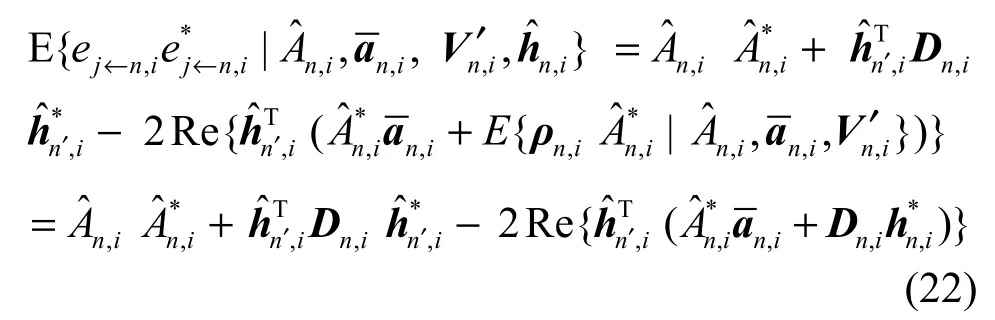
由于hn,i未知,求解时可以用n-1,i来近似,因此式(22)可以近似表示为
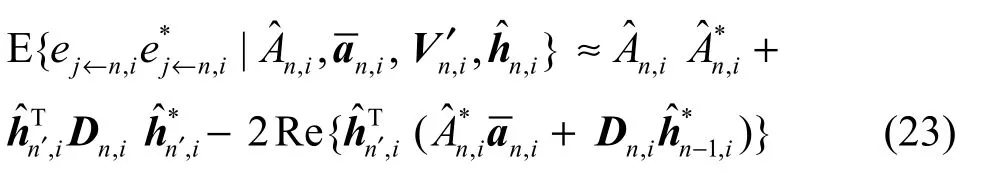
将式(23)代入式(19)并使该代价函数最小化可得信道估计值。
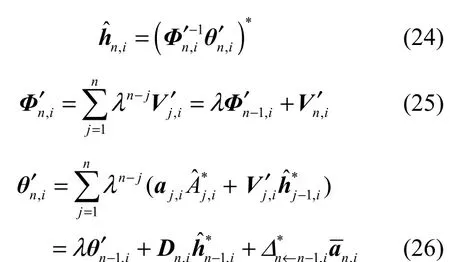
利用文献[7]给出的计算SISO均衡器输出软信息的方法需要知道噪声功率,而当利用信道估计值计算FMT解调输出时,式(8)所给出的模型将变为
因此,利用式(27)的模型计算SISO均衡器输出时需要计算误差信号 en←n-1,i的方差 σˆn2,i。文献
[14]给出了一种ad hoc算法,通过式(12)定义的误差 Δn←n-1,i来计算 en←n-1,i的方差 σˆn2,i。为了便于表述,en←n-1,i简化表示为en,i,Δn←n-1,i简化表示为Δn,i。
该算法可以简述如下。
step 1 初始化

其中,ε为常数。
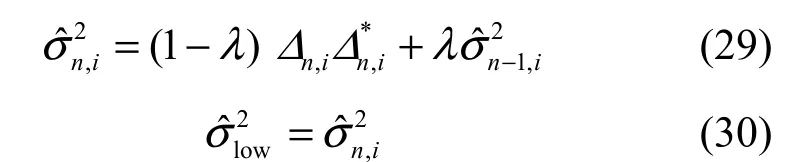
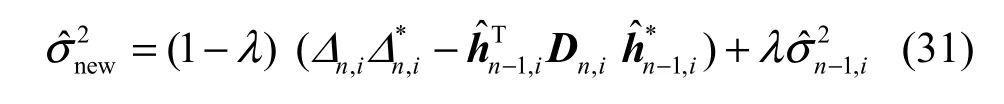
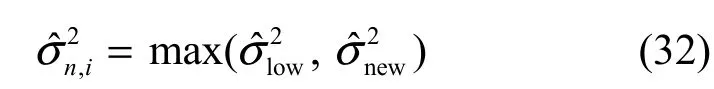
为了简化计算,在此假设误差 en←n-1,i相互不相关,并且与发送数据 An,i也不相关。因此,根据文献[7]所给出的计算均衡器输出软信息的方法,图2中SISO均衡器输出软信息为
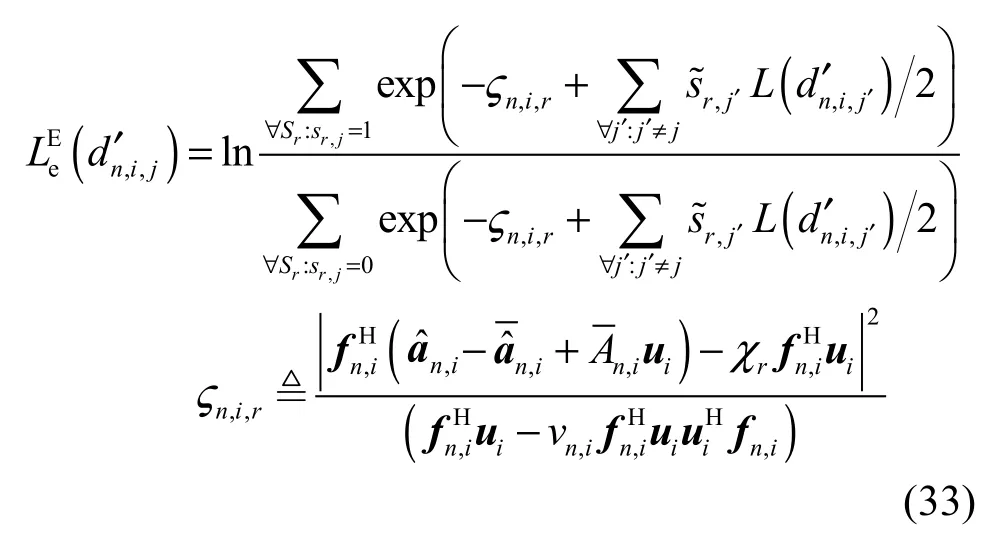
其中,
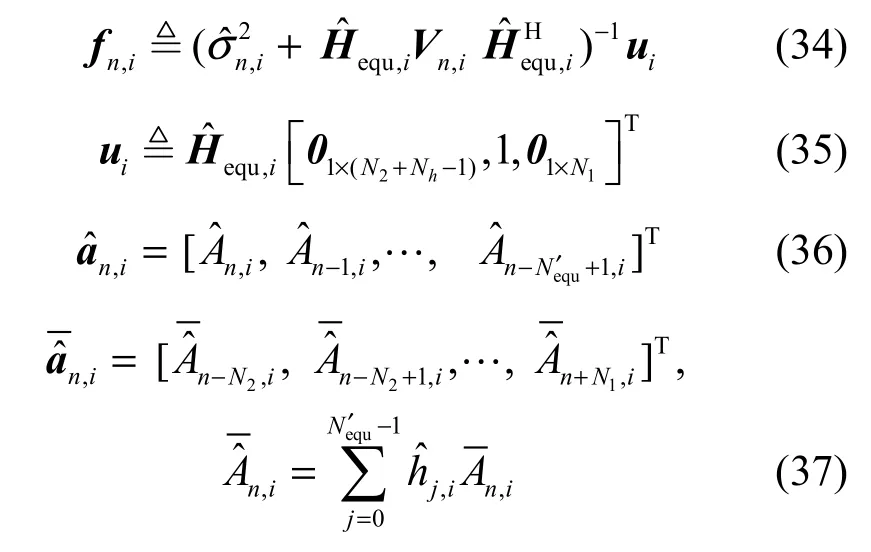
N1为均衡器非因果部分长度,N2为均衡器因果部分长度,均衡器长度为NE=N1+N2+1。equ,i为根据第 i个子信道等效冲激响应估计值所构成的NE×(NE+N'equ-1)维矩阵。
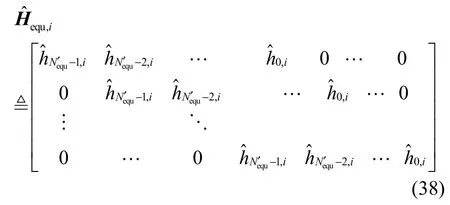
每个子信道SISO均衡器输出关于dn′,i,j的外信息经并/串变换、解交织后作为SISO译码器的输入,而译码器输出经交织和串/并变换后作为信道估计和均衡的先验信息,从而实现迭代信道估计和均衡。关于译码算法已有较多文献进行了研究[15],在此不再赘述。当迭代完成后,根据 SISO译码器输出的码元LLR来判决所接收的信号,当码元的LLR大于0则判决为1,小于0则判决为0,从而完成Turbo均衡。
4 仿真与分析
在 MATLAB仿真环境下分别对论文所提出的FMT子信道Turbo迭代均衡算法进行了仿真,并与DFE均衡算法进行了比较。仿真参数选取如下:FMT子信道数 M=64,采样因子 K=80,原型滤波器采用均方根升余弦滤波器,滚降因子 a=0.1;信道选用文献[16]中的 HiperLAN/2—Model A 和Model E模型,Model A是典型的办公室环境,RMS=50ns,Model E是典型的户外环境,RMS=250ns;编码器为(7,5)8的RSC码,码率为1/2;交织器为随机交织器,交织深度为4 096;译码器采用 Log-Map译码算法[15];DFE前馈均衡器长度Nf=5,反馈均衡器长度Nb=5;基于Turbo均衡算法的参数 N1=5,N2=5;每帧数据中训练序列长度NTr=500,NData=5 000。
图3和图4分别给出了QPSK调制和16QAM调制方式下FMT系统联合迭代信道估计和Turbo均衡在Model A信道条件下的性能。由图3可知,当调制方式为QPSK,误码率为10-4时,Turbo均衡经过2次迭代后的BER性能较之DFE均衡改善了1.5dB,经过5次迭代后的性能则改善了 4dB;而当调制方式为16QAM,误码率为10-3时,由图4可知,Turbo均衡经过2次迭代后的BER性能与DFE相当,略微改善了0.5dB,但经过5次迭代后的性能则改善了3dB。
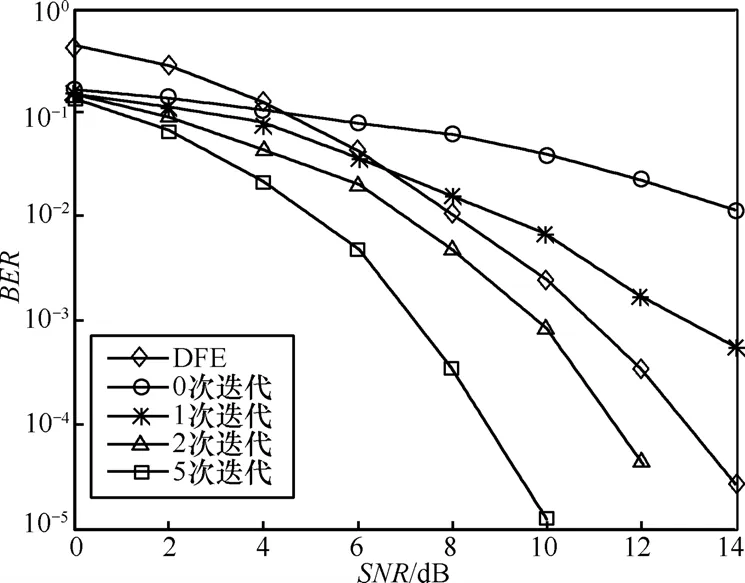
图3 QPSK调制BER性能曲线(Model A)
图5给出了采用QPSK调制时,FMT系统联合迭代信道估计和Turbo均衡在Model E信道条件下的性能。由图5可知,当误码率为10-4时,Turbo均衡经过2次迭代后的BER性能较之DFE均衡改善了2dB,经过5次迭代后的性能则改善了5dB。
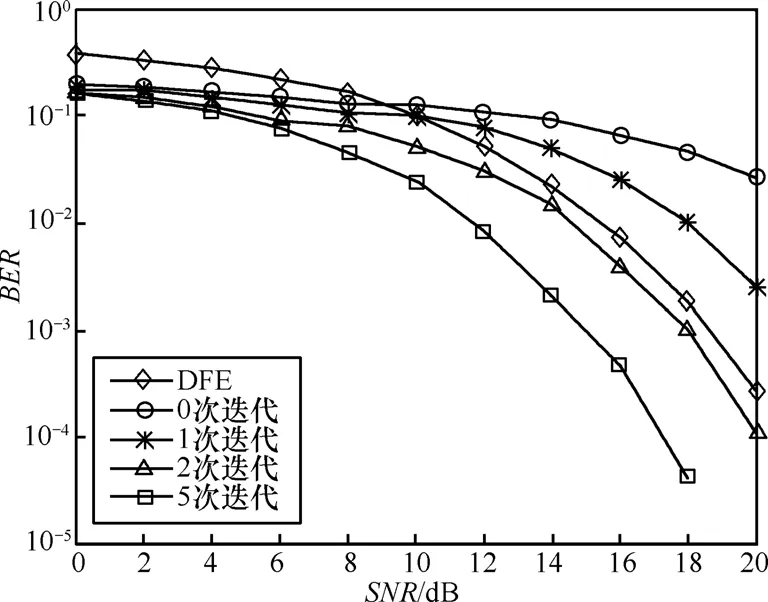
图4 16QAM调制BER性能曲线(Model A)
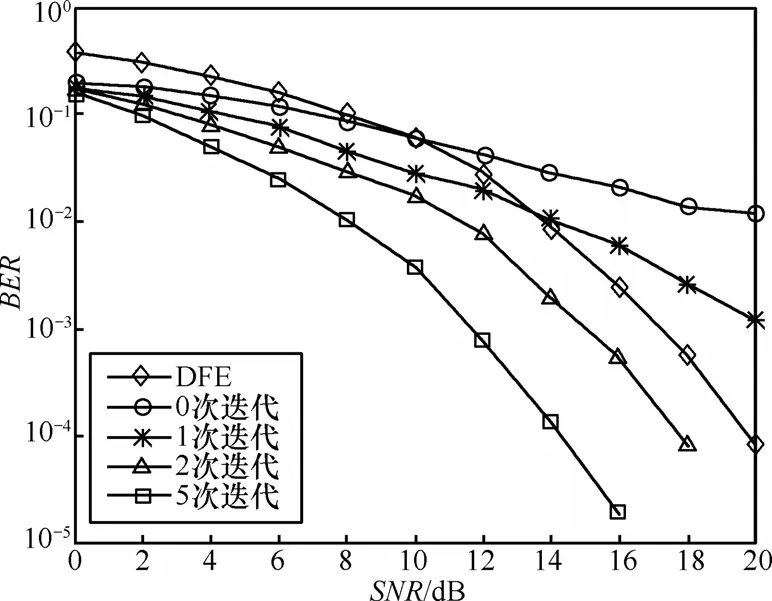
图5 QPSK调制BER性能曲线(Model E)
图6给出了SNR为12dB,调制方式为QPSK,采用 Model A信道模型时算法仿真所消耗时间的对比。由图6可知,Turbo均衡2次迭代仿真所需要的时间是DFE均衡的3.2倍,而经过5次迭代的时间是DFE的8倍,那是由于Turbo均衡需要对同一帧数据进行多次迭代处理来改善性能,但随着硬件技术的发展,系统实现复杂度的问题将得到缓解。此外,由图3~5可知,随着迭代次数的增加,其BER性能改善幅度也将逐渐降低。因此,FMT系统联合迭代信道估计和Turbo均衡的迭代次数也应该限制在5次以内。
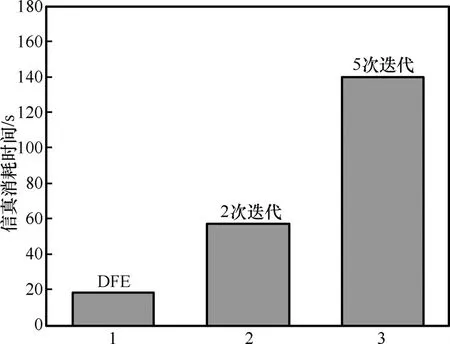
图6 仿真所消耗时间对比
5 结束语
本文将基于软信息的迭代信道估计算法应用于 FMT系统,提出了一种联合迭代信道估计和Turbo均衡的FMT系统接收方法,通过对FMT系统每个子信道的等效冲激响应进行迭代估计,然后采用基于线性滤波器结构的 Turbo均衡器来消除ISI。仿真结果表明,不论采用QPSK或16QAM调制方式,经过 2次以上的迭代后,新算法的 BER性能都优于传统的DFE均衡算法。Turbo迭代思想在无线通信系统中有着广泛的应用,本文只将该思想应用于 FMT系统的均衡,在后续研究工作中,还需要重点关注以下2方面的问题:①在不降低系统性能的前提下,如何简化系统的实现结构和算法;②如何将Turbo迭代思想应用于FMT系统设计中。
[1] CHERUBINI G,ELEFTHERIOU E,OLCER S.Filtered multitone modulation for VDSL[A].Proc IEEE Globecom’99[C].Rio de Janeiro Brazil,1999.1139-1144.
[2] BORNA B,DAVIDSON T N.Efficient design of FMT systems[J].IEEE Transactions on Communication,2006,54(5): 1413-1418
[3] TENELLO A M,PECILE F.Analytical results about the robusteness of FMT modulation with several prototype pulses in time-frequency selective fading channels[J].IEEE Transactions on Wireless Communications,2008,7(5):1634-1645.
[4] FUSCO T,PETRELLA A,TANDA M.Blind CFO estimation for noncritically sampled FMT systems[J].IEEE Transactions on Signal Processing,2008,56(6):2603-2608.
[5] BENVENUTO N,TOMASIN S,TOMBA L.Equalization methods in OFDM and FMT systems for broadband wireless communications[J].IEEE Transactions on Communications,2002,50(9):997-1015.
[6] YANG Z G,WANG X D.Turbo equalization for GMSK signaling over multipath channels[J].IEEE Journal on Selected Areas in Communications,2001,19(9): 1753-1763.
[7] TÜCHLER M,SINGER A C,KOETTER R.Minimum mean squared error equalization using a priori information[J].IEEE Transactions on Signal Processing,2002,50(3):673-683.
[8] 金国平,丁宏,钟华等.FMT系统中一种新的信道估计算法[J].信号处理,2009,25(5): 811-815.JIN G P,DING H,ZHONG H,et al.A new channel estimation algorithm for FMT system[J].Signal Processing,2009,25(5): 811-815.
[9] 金国平,钟华,郑林华.FMT频域信道估计算法的研究及其性能分析[J].计算机工程,2009,35(10):98-100.JIN G P,ZHONG H,ZHENG L H.Research of channel estimation in FMT frequency domain and its performance analysis[J].Computer Engineering,2009,35(10):98-100.
[10] SONG S,SINGER A C,SUNG K M.Soft input channel estimation for turbo equalization[J].IEEE Transactions on Signal Processing,2004,52(10):2885-2894.
[11] SELLAMI N,ROUMY A,FIJALKOW I.The impact of both a priori information and channel estimation errors on the MAP equalizer performance[J].IEEE Transactions on Signal Processing,2006,54(7):2716-2724.
[12] OTNES R,TÜCHLER M.Iterative channel estimation for Turbo equalization of time-varying frequency-selective channels[J].IEEE Transactions on Wireless Communications,2004,3(6):1918-1923.
[13] HAYKIN S著,郑宝玉 等译.自适应滤波器原理(第四版)[M].北京: 电子工业出版社,2006.HAYKIN S.Adaptive Filter Theory(The 4th)[M].Beijing: Publishing House of Electronics Industry,2006.
[14] OTNES R.Improved Receivers for Digital High Frequency Communications: Iterative Channel Estimation,Equalization,and Decoding(Adaptive Equalization)[M].Norwegian University,Science and Technology,Trondheim,Norway,2002.
[15] 刘东华.Turbo码原理与应用技术[M].北京: 电子工业出版社,2004.LIU D H.The Theory and Application of Turbo Code[M].Beijing:Publishing House of Electronics Industry,2004.
[16] MEDBO J,SCHRAMM P.Channel Models for HIPERLAN/2[R].ETSI/BRAN doc.3ERI085B,1998.

