滚动轴承寿命与可靠性试验的评定方法
张 伟,汤 洁,胡留现
(1.洛阳轴承研究所有限公司,河南 洛阳 471039;2.洛阳理工学院,河南 洛阳 471023)
轴承的寿命可靠性是轴承综合质量水平的体现,是轴承的一个重要质量指标。通过轴承的寿命可靠性试验可以反映出轴承成品以及零件的整体质量水平。轴承经过寿命与可靠性试验后,其试验数据如何评估,评定方法就显得尤为重要,且评定方法必须能体现整个行业的先进水平,需要给轴承生产企业、用户、行业及第3方认证机构一个指导性文件。
轴承行业对轴承寿命与可靠性试验评定方法的研究已有很长时间。1985年洛阳轴承研究所首次制定了滚动轴承寿命试验评定方法ZQ 37—85《滚动轴承寿命可靠性考核试验方法》,后于1991年修订为JB/CQ 37—91《滚动轴承寿命可靠性考核试验方法》,又于1997年再次修订为JB/T 50093—1997《滚动轴承 寿命及可靠性试验评定方法》。
多年来,滚动轴承寿命及可靠性试验评定方法对促进轴承寿命可靠性质量的提高、行业的质量评定以及国内、外用户的产品验收起到了重要的作用。为适应新形势下轴承质量水平不断提高的要求,以及和国外轴承质量的接轨问题,特制订GB/T 24607—2009《滚动轴承 寿命与可靠性试验及评定》标准,以促进轴承寿命可靠性质量进一步提高。
1 合格评定
轴承寿命可靠性试验原始数据经数据处理后得到相关参数,对参数进行一系列评估后才能得出合格与否。
质量要求:L10t/L10h≥Z′即为合格,其中L10t为基本额定寿命的试验值;L10h为基本额定寿命;Z′为质量系数,与轴承的结构、材料、工艺有关,球轴承Z′=1.4,滚子轴承及调心球轴承Z′=1.2。
但对具体的试验有不同的要求,最基本的验证试验达到合格寿命即认为合格;而鉴定试验要求达到合格寿命的3倍为合格。
如果是长寿命试验时,还应给出达到合格倍数的值,即达到L10t/L10h的倍数值。
2 试验数据处理
常规试验数据处理一般依据二参数Weibull分布函数,使用图估计法和参数估计法进行分析处理。其中,图估计法较简便直观,一般可优先采用;而对试验数据较少或无失效数据的情况一般采用序贯试验评定方法。
2.1 Weibull分布图估计法
2.1.1 图估计目的
通过对轴承样品的完全试验、截尾试验等,得出试验数据,根据图估计法在Weibull分布图上估计出分布参数,并得出试验结果及评定结果。
2.1.2 Weibull分布图
轴承寿命服从二参数Weibull分布函数:
其对数形式为:

则上式变成直角坐标系中一条直线方程:
Y=bX+B。

轴承寿命Weibull分布曲线是以b为斜率,ν为特征寿命的一条直线,b表示轴承寿命的离散程度或轴承寿命质量的稳定性,斜率b越大,说明轴承寿命数据较集中,轴承寿命质量稳定;反之则说明轴承寿命数据离散,轴承寿命质量不稳定。ν是当F(ν)=0.632时的轴承寿命,即破坏概率为63.2%时的轴承寿命。求出参数b,ν,直线可唯一确定。
2.1.3 一般的图估计
一般对于失效数据不少于6个的试验数据评定,可用图估计方法。失效数据越少,图估计的精度就越低。

由直线求出参数b,ν,再分别求出基本额定寿命的试验值L10t(纵轴为10%),中值额定寿命的试验值L50t(纵轴为50%),计算出可靠度Re等。
2.1.4 分组淘汰图估计
分组淘汰试验方法可缩短试验周期,但试验风险比一般完全试验和定时(数)截尾试验大。试验中,每一分组中出现一个失效样品即停止试验,然后用各组的最短寿命数据在Weibull分布概率纸上描点,配置直线,再由该直线求得该批样品的分布直线。
2.1.5 图估计实例
例1:某厂生产的深沟球轴承L10h=100 h,N=8套,试验结束,得到8个失效数据,分别是80,110,155,170,220,240,300和380 h。用Weibull分布图估计参数b及ν,L10t,L50t,Re等值。
(a)由8个失效数据,配置直线A(图1)。

图1 Weibull分布图估计

(b)由直线A求出:b=2,ν=250 h,L10t=85 h,L50t=200 h,Re=86%。
(c)L10t/L10h=85/100<1.4,故判定该批轴承样品不合格。
例2:某厂生产的深沟球轴承L10h=100 h,N=32套,分8组(m=8),每组4套同时上机试验N′=4套。每组有一套轴承失效即停机,试验结束,得到8个分组的最短寿命分别为80,110,155,170,220,240,300和380 h。用Weibull分布图估计参数b,ν,L10t,L50t,Re等值。
本例为分组淘汰图估计例。先按例1求出分布直线A,再由分布直线A求分布直线B。

(b)作3条平行线:过F(L)=50%作横轴平行线与直线A交于点C,过C作纵轴平行线与过F(L)=0.159的横轴平行线交于点M。(在直线A上取纵坐标为F(L)=50%的点C,由C做纵轴平行线,并与过F(L)=0.159的横轴平行线交于点M。)
(c)过M点做平行于直线A的平行线B。

由直线B求出:b=2,ν=500 h,L10t=160 h,L50t=400 h,Re=96%。
(d)L10t/L10h=160/100>1.4,故判定该批轴承样品合格。
2.2 Weibull分布参数估计
2.2.1 Weibull分布参数估计的目的
通过试验轴承样品的完全试验、截尾试验,得出试验数据,根据Weibull分布数据处理估计出分布参数,并得出试验结果及评定结果。
截尾试验失效数据一般应不少于6个。若失效数据太少,参数估计的精度就会降低。
通过数据处理确定Weibull分布的两个参数b,ν。
设样本容量为N,经试验后得到的实际寿命为:
完全试验L1≤L2…≤Li…≤LN,i=1,2,…,N。
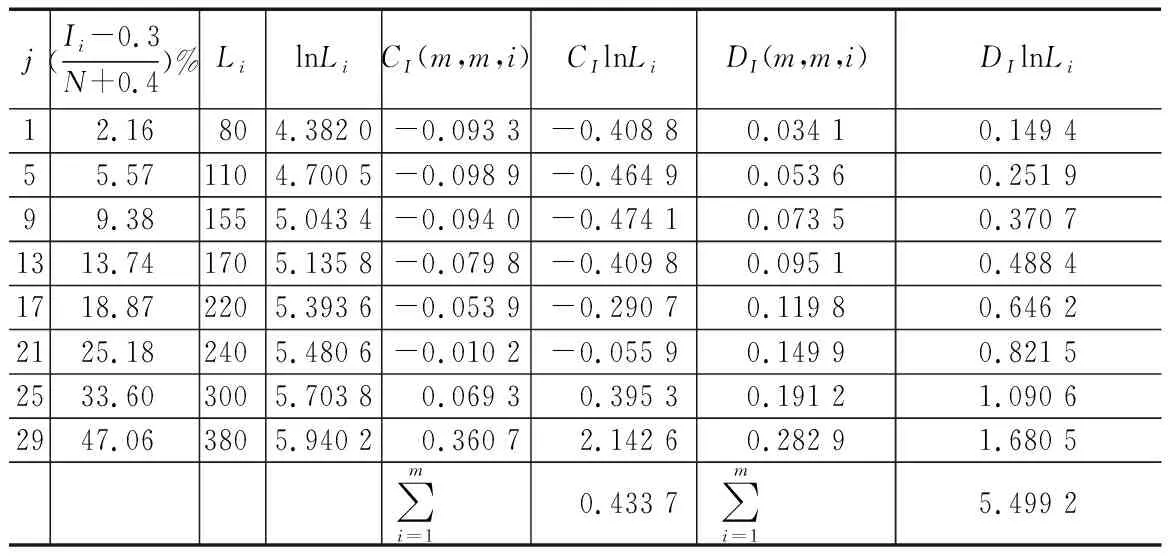
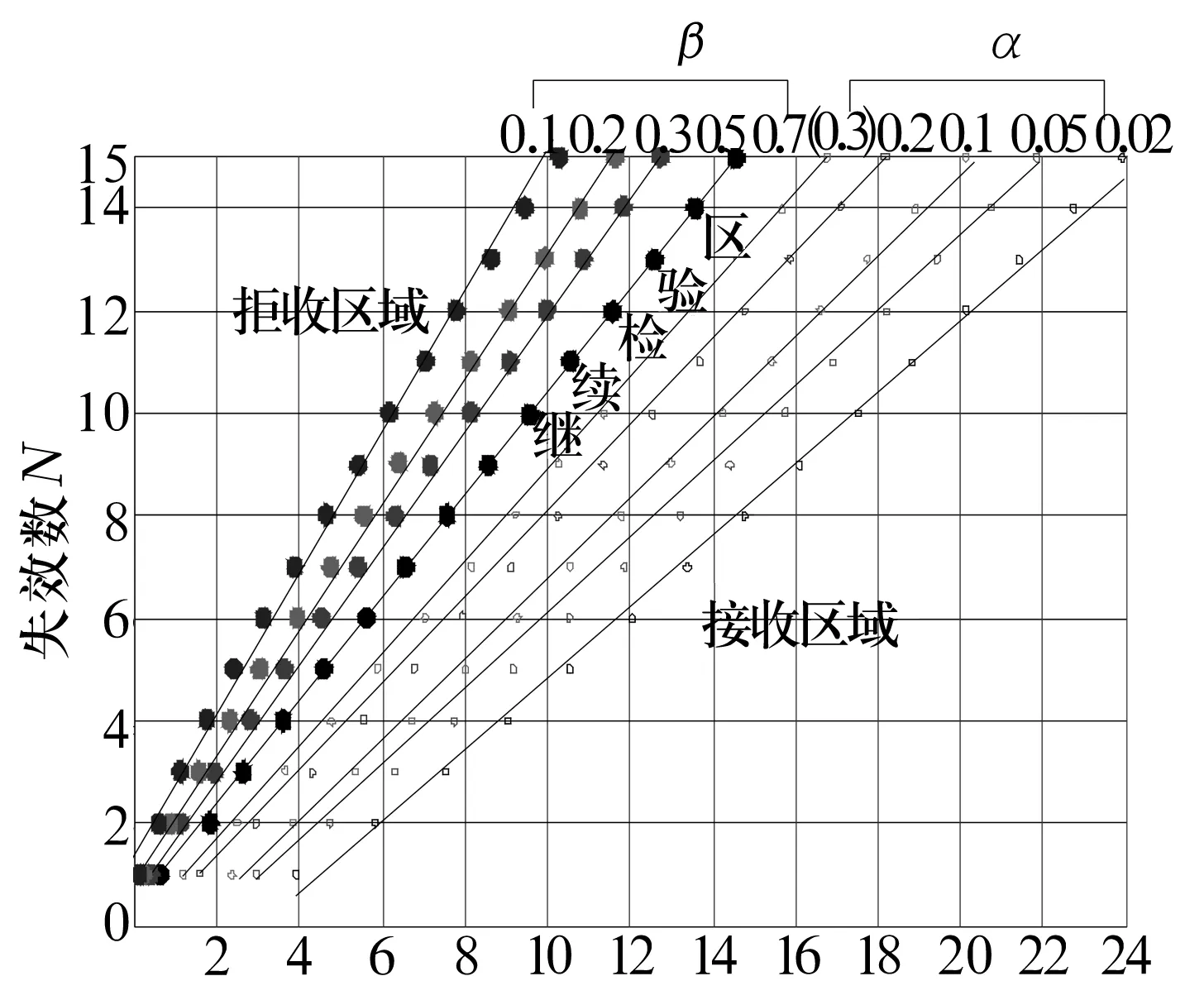
定数截尾试验L1≤L2…≤Li…≤Lr,i=1,2,…,r;r 分组淘汰试验L1≤L2…≤Li…≤Lm,i=1,2,…,m;m=N/N′。 表1 非完全试验时F(Li)的修正值 轴承寿命Weibull分布参数b,ν的估计,当N≤25时,用最佳线性不变估计(BLIE)方法;当N>25时,用最大似然估计(ML)方法(略)。 2.2.2 最佳线性不变估计 完全试验: 定数截尾试验: 分组淘汰试验: 最佳线性不变估计系数CI,DI见《可靠性试验用表》。 2.2.3 依据b,ν估计L10t,L50t及Re 当F(L)=0.10时,基本额定寿命的试验值L10t=ν(0.105 36)1/b; 当F(L)=0.50时,L50t=ν(0.693 15)1/b; 2.2.4 参数估计实例 例3:对例1的数据用Weibull分布估计参数b及ν,并计算L10t,L50t,Re等值。 本例为完全试验,最佳线性不变估计系数为CI(N,N,i),DI(N,N,i)。 若为定数截尾试验,失效数一般不能少于试验样品容量的2/3,即r 参数估计列于表2,计算得:b=2.305 7,lnν=5.499 2,ν=244.5 h,L10t=92 h,L50t=210 h,Re=88%。 表2 Weibull分布参数估计表 L10t/L10h=92/100<1.4,故判定该批轴承样品不合格。 例4:对例2的数据用Weibull分布估计参数b及ν,并计算L10t,L50t,Re等值。 对样本容量为N的试验样品进行试验时,因为有各种各样的原因使某一试样中停试验,此数据就是未失效数据(按数据大小排列,未失效数据可能在失效数据之间),一般数据处理方法是不考虑未失效数据,这样就不能真实地反映整体的情况,影响轴承质量水平评价。所以含有未失效数据的处理要对失效数据进行位置修正。 非完全试验F(Li)的修正值的计算见表1。最佳线性不变估计系数为CI(m,m,i),DI(m,m,i),参数估计见表3。 表3 非完全试验Weibull分布参数估计表 b=2.305 7,lnν=6.100 4,ν=446 h,L10t=170 h,L50t=380 h,Re=97%。 L10t/L10h=170/100>1.4,故判定该批轴承样品合格。 本标准所选取的后验序贯抽样检验方案,是序贯抽样检验的一种。其适用性强,可利用原有试验设备,特别是当疲劳破坏数据较少时,也可给出判定结论,便于考核及订户验收;而且方法简便,运算少,数据处理程序化、表格化,便于推广应用。 完全试验、截尾试验一般需要较长试验时间才能得出结果,而对小子样失效数据、无失效数据的处理宜采用序贯试验,较短时间就能得出结果。 序贯试验用于试验设计而不是试验判定。第1套轴承如果出门,则直接判定合格;如果不入门,则判定为不合格;如果在继续检验区,则用替换轴承继续检验。 2.3.1 替换试验 试验采用有替换试验序贯检验,按失效顺序逐套进行检验判定。当有5套轴承样品失效时停试,并做出合格与否的判定。试验中替换轴承样品的失效数据也参与判定。这种方法用于小子样或无失效数据的处理。 2.3.2 检验判定参数 综合国内、外资料,取Weibull分布斜率b=1.5。 检验水平:根据选取的α,β风险值分为4组,检验水平由宽到严。一般用户验收的试验取水平Ⅰ或Ⅱ,行业及第3方认证机构的试验取水平Ⅱ或Ⅲ,制造厂内部的试验取水平Ⅲ或Ⅳ,如表4所示。 表4 检验水平 α为合格风险,接受风险或显著性水平,1-α为置信度。 β为不合格风险,拒绝风险。本标准判定检验时配合α使用。有时称β为使用方风险。 2.3.3 检验判定门限 不同的α,β值可以组成多个检验水平,图2为不同检验区示意图。由图可以看出,水平Ⅰ,Ⅱ,Ⅲ接受区一样,但拒收区增加,即继续检验区减小;水平Ⅳ接收区减小,拒收区增加。这样从检验水平Ⅰ→Ⅳ,检验水平逐步加严。 图2 检验区示意图 与表4中α,β对应的门限系数μα,μβ见表5。从图2及表5看出,如果取α=0.3,β=0.7,即两条检验判定线重合,说明检验严,要么合格,要么不合格,中间没有继续检验区。 表5 与α,β对应的门限系数μα,μβ值 表中给出了一个i=0的点,在判断格式里为t10点,即无失效门限t10,r=0时的接受门限值,该点尤其适用于军品轴承试验套数少,而又要求无失效试验的特点。 2.3.4 检验判定格式 表6 检验判定格式 2.3.5 检验判定式 若0≤i<5,Ti>t1i为合格(接受);Ti 若i=5,t15-T5≤T5-t25为合格;否则为不合格。 2.3.6 可靠度Re 2.3.7 序贯试验实例 圆锥滚子轴承质量要求:L10t/L10h≥Z′为合格,Z′为1.2。 计算t1i及t2i,其检验判定格式见表7。 表7 检验判定表 情况1:当试至200 h,尚无失效轴承出现,这时12套轴承均试至200 h。 判定该批轴承样品合格。 (100+180]1.5/121.5=2801.5=4 685,t22 3 336 当试至455 h,第3套轴承失效,L3=455 h,T3=4551.5=9 705>t13=9 612,合格停试。 判定该批轴承样品合格。 情况3:当L1=180 h,T1=1801.5=2 414,t21 当L2=220 h,T2=2201.5=3 263,T2 判定该批轴承样品不合格。 情况4:如果是长寿命试验时,还应给出达到合格倍数的值(K值),即达到Z′的倍数值;相应的可靠度Re等。 若12套轴承试至500 h均无失效,则: 设K=3,则t10=8 418,合格;K=4,则t10=11 225,不合格。 假设某轴承L10h=100 h,N=12套和N=8套,b=1.5,在不同质量系数、不同检验水平风险时的最小无失效时间比较见表8。 表8 最小无失效时间比较 由于序贯试验风险较大,所以判定加严。 N=12套时,球轴承Z′=1.4,检验水平α=0.2,β=0.3,最小无失效时间约比L10h增大50%;滚子轴承Z′=1.2,检验水平α=0.2,β=0.3,最小无失效时间约比L10h增大30%。 对图估计、参数估计,球轴承L10t/L10h≥1.4为合格,即超过L10h的40%为合格;滚子轴承L10t/L10h≥1.2为合格,即超过L10h的20%为合格。 由于序贯试验风险较大,相比较其判定均比图估计、参数估计加严一定的比例。故3种数据处理结果基本一致。 N=12套时,球轴承Z′=1.4,检验水平α=0.2,β=0.3,最小无失效时间为148 h;Z′=1.05,检验水平α=0.3,β=0.3,最小无失效时间为100 h,两者相差约50%。 滚子轴承Z′=1.2,检验水平α=0.2,β=0.3,最小无失效时间为133 h;Z′=1,检验水平α=0.3,β=0.3,最小无失效时间为97 h,两者相差约40%。 相同质量系数、检验水平下,试验套数N=8较N=12的试验时间长约30%,即试验套数减少,试验风险将增加。 对于轴承寿命与可靠性试验,如果失效数据不少于6个,试验评定采用Weibull分布图估计、参数估计,可以给出试验评定结果;对于小子样失效数据、无失效数据的处理则采用序贯试验,较短时间就能得出评定结果,可以大大提高试验的效率。





2.3 序贯试验方法











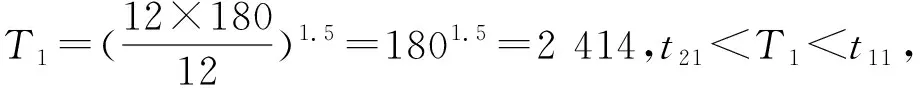



3 试验验证

3.1 序贯试验与图估计、参数估计比较
3.2 不同质量系数、不同检验水平比较
3.3 不同试验套数比较
4 结束语

