结构变形对测向天线精度的影响
李聪聪,刘国玺,毛贵海
(中国电子科技集团公司第五十四研究所,河北石家庄050081)
0 引言
在无线电导航、电子侦察、电子跟踪和电子对抗等电子系统中,一个很重要的任务是测定目标的方位[1]。测向的方法和种类很多,按天线的方向图大体可分为两类。一种是利用简单振子或天线阵列的一定方向性来测向;另一类是利用系统功能来测向,而对天线方向图没有特殊要求。前者如由垂直振子天线与环形天线组合的复合天线,这个复合天线将会产生一心形方向图。通过旋转天线可找出某一方位天线感应电压最小。这种方式的测向的优点是:天线结构简单,尺寸小。缺点是:工作带宽窄,测向精度低。而后一类采用干涉仪测向体制,具有适用于任意形状的天线阵列、测向精度高等优点,广泛应用于无线电通信侦察、电磁频谱监测、导航、射电天文等领域。其中,圆形阵列是目前应用最普遍的干涉仪测向体制。
评价测向系统性能的主要技术指标是灵敏度、测向精度和抗干扰性能。
1 测向原理
1.1 干涉仪原理
干涉仪原理是利用信号到达固定间距天线阵列中不同天线振子的时间先后所形成的相位差来判断来波方位的一种测向方法,它是目前世界上最先进的测向机制。图1为测向原理图。

图1 测向原理图
如图1所示,间隔为 d(称为基线)的2个偶极子天线1和2,来波方向与d的垂直平分线的夹角为θ,此时信号到达2个天线振子时就会有相位差,如以天线1为计算相位差的基准天线,波程差与相位分别为:

式(1)、式(2)中 d21和 φ21分别表示天线2相对于天线1的波程差和相位差,λ为来波波长。令:

由式(2)可得:

由式(4)可知 n值越大,φ21对 θ的灵敏度就越高,测向精度也越高。但是,n值越大,θ值越容易超过2π的范围,从而引起测量相位差的模糊。为了解决解相位值模糊这一矛盾,可增加单元天线组数。
1.2 测向算法
实际测向天线采用五阵元体制,如图2所示。
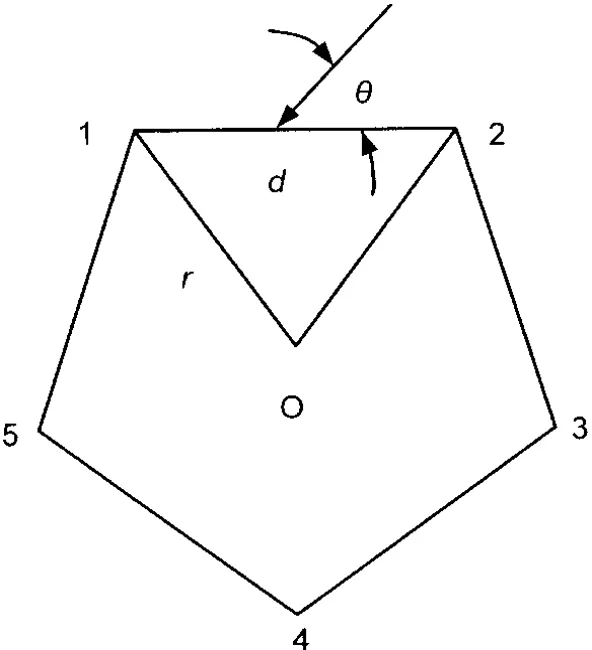
图2 五阵元测向体制图
图2中,边长为d,则各单元天线之间的波程差为:

各单元天线相对应的相位差为:
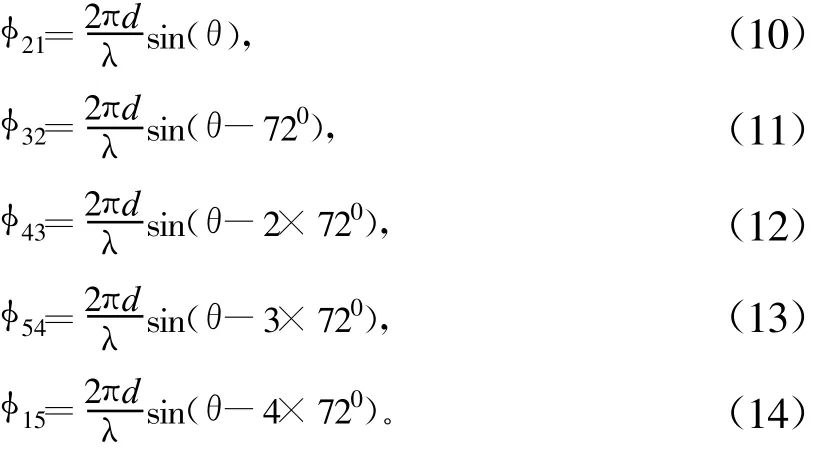
由式(10)~(14)可以看出:各单元天线的间距将影响天线的测向精度。因此,有必要分析间距误差对相位的影响。
2 受力与误差分析
2.1 受力分析
一般情况下,天线所受的载荷主要包括:自重和风负荷。自重主要引起各单元天线在垂直平面内的微小位移,但我们注意到:各单元天线为全向,因此,自重变形不会对天线的测向精度产生影响。风负荷则不同,它将影响天线的测向精度。
风力计算的公式可写为:

式中,v为风速,CF为风力系数,A为物体的特征面积。风力作用于各基线的横向力分别为:

对于各集合线的载荷集度为:

式(21)中,Fi为各基线所受的横向力,r为基线半径。基线受力示意图如图3所示。
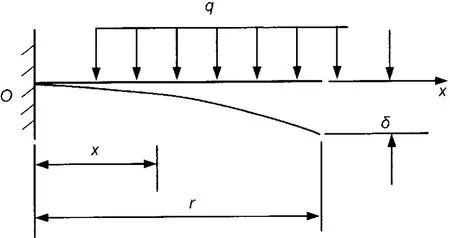
图3 基线受力示意图
则距离原点为 x的截面的弯矩为:

根据变形物体的挠曲线微分方程:
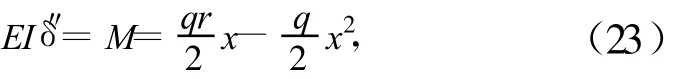
式(23)中,E为弹性模量,I为惯性矩,δ″为变形的两阶导数。
经过两次积分可得:

再由边界条件原点处的转角和挠度应等于0,即当 x=0 时 ,δ′=0,δ=0。
则式(24)、式(25)中的常数 C、D 均为 0。式(25)变为:
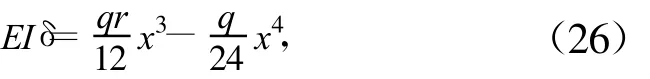
由式(26)可以看出当给定r时,即可求出该处的挠度。
2.2 变形计算
现以某工程的测向天线为例来计算单元振子之间的间距误差。取1号和5号基线为例。由式(26)可得出 δ1=0.071 mm,δ5=0.054 mm。再经过转化振子间的距离为 x=0.11 mm。
3 测向误差
以50 MHz为例来计算有间距误差和无误差时的相位曲线。
在图4、图5中θ表示来波方位角,φ表示理论相位差曲线,Δ φ表示基线在受力变形时与理论相位差之间的误差。
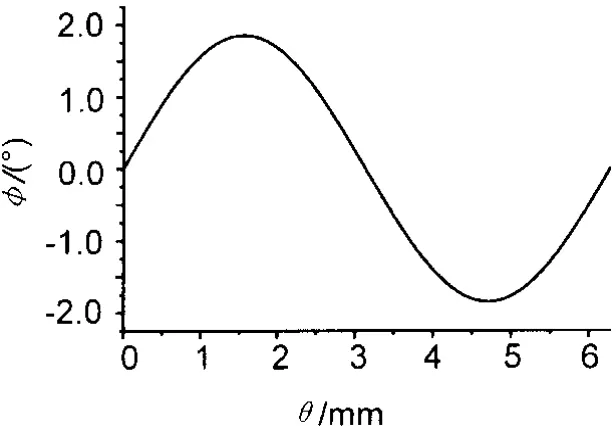
图4 无误差时的相位差曲线

图5 变形引起的相位误差
4 结束语
通过计算不同风速时单元天线的变形,进而得出修正后的各单元间的相位差,这样可以作到有的放矢,同时,将各种情况加入到系统的相关表中,来提高测向天线在不同工况时的测向精度。
[1]林昌禄.近代天线设计[M].北京:人民邮电出版社,1987.
[2]刘鸿文,材料力学[M].北京:高等教育出版社,2004.
[3]TITZE W A U.Direction Finding System Using Symmetricpair Anntenna Arrsys[J].IEEE proc.Radar,Sonar Navig.,1995,142(3):130-136.
[4]周朝栋.天线理论与工程[M].西安:西安电子科技大学出版社,1988.

