降低OFDM系统峰均功率比的研究

段再超,肖丽萍

(燕山大学信息科学与工程学院,河北秦皇岛066004)

0 引言

OFDM(正交频分复用)是一种多载波调制技术,目前已经成功应用于无线局域网IEEE802.1la,HYPERLAN和数字视频广播(DVB)等系统中。但是由于OFDM信号是多个独立的信号直接叠加而成,具有很高的峰均功率比,为避免信号非线性失真必须采用具有大动态范围功率放大器,同时放大器的效率也会降低,且高的峰均功率比值也要求A/D、D/A转换器具有非常大的动态范围,因此增加了系统的造价和实现难度。

为解决OFDM系统中高的PAPR的问题,近年来国内外此方面的研究人员提出了很多降低峰均功率比的方法,包括限幅类技术[1]、概率类技术[2]、星座图类技术[3]、编码类技术[4]、载波干涉技术[5]等。载波干涉的方法是通过改变OFDM信号的统计特性来降低系统峰均功率比值。基于载波干涉的OFDM系统(即 CI/OFDM)不仅可以有效地降低系统的PAPR,而且能凭借扩频带来的频率分集效应提高系统的误码率性能。CI/OFDM系统具有应用灵活,易于与其他降低 PAPR技术结合使用,复杂性也比较低的优点,因此具有很高的实用价值。文中对载波干涉法进行了改进,在保证误比特性能的前提下,进一步降低了PAPR。

1 OFDM系统及载波干涉

1.1 OFDM系统

在OFDM系统中,已调制的OFDM信号可以表示为[1]：

式中,N为载波数,TS为OFDM符号宽度,Δf=1/Ts为子载波频率间隔,a[k](k=0,1,…N-1)为输入数据符号。s(t)的离散形式s(n)可表示为：

由于OFDM符号是由多个独立的经过调制的子载波信号相加而成的,这样的合成信号就有可能产生比较大的峰值功率(peak power),由此会带来较大的峰值平均功率比(peak-to-average power ratio),简称峰均比(PAPR)。峰均比可以被定义为：

在实际应用中,通常采用峰均功率比超过某一门限值δ2的概率,即互补累积分布函数(CCDF)来衡量OFDM系统的PAPR分布,即：

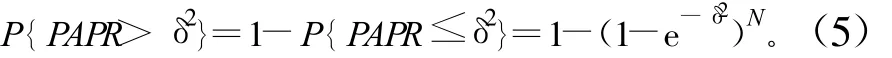
由上式可见,子载波数 N增大时,P{PAPR＞δ2}也随着增大。

1.2 载波干涉

载波干涉技术是一种已被前人仿真证明具有可行性的新方案。载波信号是矩形函数的频域离散采样表示形式,在时域上是个周期的sinc函数。将每个低速并行数据均由正交的CI码扩展到OFDM的全部子载波上同时传输,不降低系统传输率即可产生频率分集效应。凭借它的频率分集特性可以有效克服无线通信中的多径衰落。CI码还能使每个数据调制的时域波形峰值均匀错开,从而很好地降低了PAPR。CI/OFDM发射机结构如图1所示。

图1 CI/OFDM系统发送端原理图

由图1可知,与传统OFDM不同的是经过串并转换的数据,不是分别调制到相互正交的子载波上,而是调制到相互正交的CI信号上,然后合成,经上变频后进行传输。CI信号由加载了CI扩展码的N个相互正交的子载波组成。

CI/OFDM发送信号可表示为：

式(6)中 ak表示发送的第k个数据,iΔθk表示ak所对应CI码在子载波 i上的码元,fi=iΔf,Δf=1/Ts为子载波频率间隔,fc为载频。因为带通信号的峰值功率近似等于信号包络的峰值功率,而前者的平均功率是后者的一半,两者峰均功率比相差3 dB,在研究中只需要考虑基带信号的峰均功率比即可。所以忽略载频fc的影响,其复基带信号可表示为：

式(7)中,Δθk=,k=0,1,…,N-1,实现了各个子载波调制的相位补偿,它们之间也是相互正交的。定义第k个数据调制的CI信号为：

C(k)={ej◦0◦Δθk,ej◦1◦Δθk,…,ej◦(N-1)◦Δθk},k=0,1,2,…,N-1,则CI信号可表示为：

在一个OFDM符号持续时间内,各CI信号的主瓣互不重叠,彼此保证特定的延时关系时,某一CI信号峰值点都对应着其他CI信号的零点,从而采样时不存在信号间的干扰,保证了各CI信号之间的正交性。并使得所有数据符号的能量在整个OFDM符号持续时间内得以均匀分布,从而大大降低了CI/OFDM系统的峰均功率比。因此,在BPSK调制情况下,CI/OFDM系统的PAPR同样也得到了大大的降低,即：

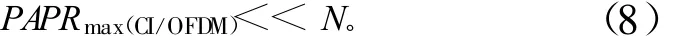
2 对载波干涉的改进

从式(5)可理论分析得知使 PAPR值变大的原因是由于在进行IFFT快速反傅里叶变换时,将 N个子载波相加导致了较大的PAPR值出现,且P PAPR＞δ2随N增大而增大,因此可以通过降低一个IFFT内的子载波数来达到降低PAPR的目的。现将 N个子载波分成M组,分别送入 M个IFFT变换器进行变换。由于每组的IFFT计算分别进行,这样每一组输入到IFFT的子载波数就会降低,达到降低每一组PAPR值的目的。同样,接收端每一组的子载波与相应的CI解扩码进行操作。为了达到最佳效果,每组采用相同的值m,即为m=N/M。将改进后的CI/OFDM发送原理图如图2所示。

第1组的子载波分别为(a0,a1,…,am-1),第2组的子载波分别为(am,am+1,…,a2◦m-1),……,第M 组的子载波分别为(a(M-1)◦m,a(M-1)◦m+1,…,aN-1),分组后的信号为：

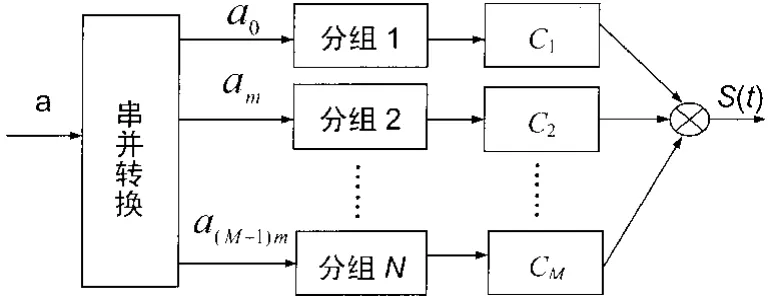
图2 发送端、接收端的部分框图

分组后的信号s(t)的最大值随着分组后每组的子载波个数减少而降低,而 s(t)的平均功率E{s(t)2}不发生改变,则：

因此,改进的方法较CI/OFDM能进一步地降低PAPR。

3 仿真与性能分析

文中采用子载波数为32,调制方式为BPSK的OFDM信号,对CI/OFDM及提出的方法的互补累积分布函数(CCDF)与误码率(BER)性能进行了仿真,仿真结果如图3和图4所示。

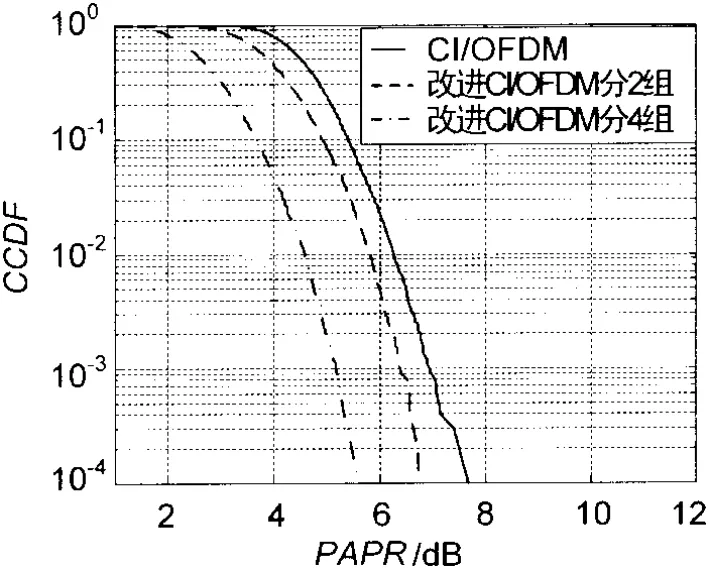
图3 CCDF曲线对比图

图3给出了采用4倍过采样时载波干涉法以及文中方法的CCDF曲线。由图3可见,改进后的方法与未改进的方法相比PAPR有了明显的降低,例如在CCDF为10-4时,将输入信号分为2组时PAPR改进了0.65 dB,将输入信号分为 4组时PAPR改进了1.85 dB。由此可见,分组数越多,PAPR降低效果越明显。

图4给出了在加性高斯白噪声(AWGN)信道的条件下,载波干涉与改进方法的 BER性能仿真曲线。仿真结果表明,改进后方法的BER性能与原载波干涉法的BER性能十分接近,表明该方法在有效地降低OFDM系统的 PAPR的同时保证了系统的BER性能。

图4 BER曲线比较图

4 结束语

文中对现有载波干涉降低PAPR技术进行了改进。即在加载波干涉之前先对输入信号进行分组,减小高峰值功率出现的概率,从而降低系统的PAPR。该技术不仅适用于BPSK调制,同样适用于其他多进制调制方式。此方案不仅算法简单、不产生失真、不发送边带信息,而且能更灵活地实现,易与其他降低PAPR技术结合使用,具有较好的实用性。

[1]XUE Kai-yuan,YANG Hong-wen,SU Sheng-lan.The clipping noiseand PAPR in the OFDM system[R].Proceedings-2009 WRI International Conference on Communications and Mobile Computing,CMC 2009：265-269.

[2]WU Xin-chun,WANG Jin-xiang.A novel PTS architecture for PAPR reduction of OFD M signals[R].2008 11th IEEE Singapore International Conference on Communication Systems.2008：1055-1060.

[3]LONGO FRANCESCO,ANSARI RASHID.Erasure pattern selection with active constellation extension forpeak-toaverage power ratio reduction in OFDM[R].2007 IEEE International Conference on Electro/Information Technology,EIT 2007：53-58.

[4]CHEN Houshou,LIANG Hsinying.PAPR reduction of OFDM signals using partial transmit sequences and Reed-Muller codes[J].Department of Electrical Engineering,Graduate Institute of Communication Engineering.2007：528-530.

[5]WIEGANDT D A,NASSAR C R,WU Z.The Elimimation of Peak-to Average Power Ratio Concerns in OFDM via Carrier Interferometry Spreading Codes：A Multiple Constellation Analysis[J].In Proceedings of the Thirty-sixth Southeastern Symposium.2004,36：323-327.