一种参数途径的自适应时延估计方法
王 江,李永生,李林果
(1.中国人民解放军电子工程学院,安徽合肥230037;2.中国人民解放军77526部队,西藏拉萨850000)
0 引言
时差定位系统具有高度的隐蔽性和精确的测向定位特性,在电子对抗侦察和定位中具有很高的应用价值,一直受到学者们的广泛关注[1-3]。时差定位系统通过估计空间来波信号到达位置分开的不同传感器的时差来对辐射源目标进行定位。因此,能否对来波信号到达不同传感器的时差进行精确估计,直接决定了时差定位系统定位精度高低。对来波信号的到达时差进行估计通常称为时延估计。时延估计的方法总体上可以分为基于信号各阶统计量方法[4-5]和自适应类的方法[6-7]。
时差定位实际应用中,需要先对侦收的连续信号进行离散采样,再做时延估计。信号到达2个传感器的时差D通常不是采样间隔T的整数倍。无论是用基于信号各阶统计量类时延估计方法,还是自适应类时延估计方法,即使在没有噪声的情况下,时延估计误差也可能达到0.5T。为减小此误差,可以通过提高采样频率即减小采样间隔T的方法,也可以用插值方法。有学者应用插值方法[8]提高时延估计精度,常用的插值方法有sinc函数插值、抛物线或其他多项式插值等。但插值方法的计算量较大,导致时延估计速度较慢,系统实时性差。
基于时延估计可以转化为对滤波器的权系数最大值的位置估计来实现,文献[9]提出了通过参数途径进行时延估计方法。参数途径时延估计方法可以直接估计非整数倍采样间隔的时差,且不需要插值运算,运算量较小。应用LMS算法来实现参数途径时延估计方法,新方法简称为P-LMSTDE,下面详细论述。
1 时延估计转换为sinc滤波器的权系数
由于2部传感器的空间距离较远,因此同一来波信号到达2部传感器有时差。假设时差为D,2个传感器输出的信号可以表示为:

式中,n1(t)和n2(t)为相互独立的零均值高斯白噪声,且与信号 s(t)相互独立。
为方便讨论,先不考虑噪声影响,定义信号u(t)和 v(t)为 :


式(5)中,

式中,T为采样间隔。不失一般性,假设时差D=(m+f)T,m是整数,f是小数,0≤f≤1。则时延信号v(t)可以重构为:

对时间t离散化,则任意整数n:

做变量代换,让 q=n-k,式(8)变为:

定义:
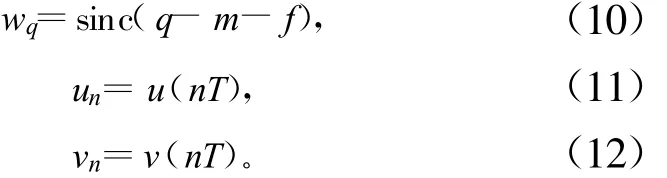
则式(9)可以改为:

由式(13)可看到,时间序列un通过一个权系数为 wq,q=-∞,…,∞ 的滤波器与其时延序列vn相联系,且与时延D有关。由于 wq是辛格函数sinc(q-m-f)的采样,当 q-m-f=0时,其取得最大值,如图1所示。因此,时延估计问题转换为寻找 wq的最大值。

图1 sinc(q-m-f)函数波形图
对式(1)和式(2)的时延估计模型进行离散采样得:

由式(13)和式(15)可得,xn和yn的关系可以表示为:
图5给出了热流密度=30W/cm2时,质量流率和微通道分支数n对最大热应力σ的影响。由图5可知,在相同微通道分支数的情况下,最大热应力σ随质量流率的增大而减小,但降幅逐渐减小。以质量流率分别为4.5g/s和1.5g/s时的最大热应力进行比较,n分别为3、4、6、8时,σ分别降低0.216、0.192、0.178、0.163GPa,降低幅度分别为54.8%、55.0%、56.9%、56.6%。即当冷却流体质量流率增大3倍时,各热沉的热应力降低超过一半,高质量流率下能够有效降低热沉热应力。
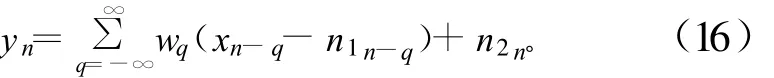

相应的式(16)变为:

式(18)中误差en由噪声成分和模型误差组成,表达式为:

有很多方法求解方程式(17),最简单的方法是应用LMS算法来估计wq,即:

2 时延估计
根据图1可得,当 f<0.5时,式(10)中 wq在q=m处达到最大值;当f>0.5时,wq在q=m+1处达到最大值。记 wj代表权系数wq的最大值,wj+1代表最大值的后一个值,wj-1代表最大值的前一个值。则当f<0.5时,可得:

式(21)除以式(22),得:

当 f>0.5时,可得:

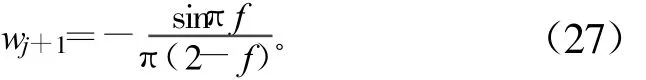
式(25)除以式(26),得:

假设经过LMS算法n步迭代后,滤波器权系数进入稳定状态。此时最大值权系数标号为wj,其后一个权系数为wj+1,前一个权系数为wj-1。则根据式(24),时延估计为:
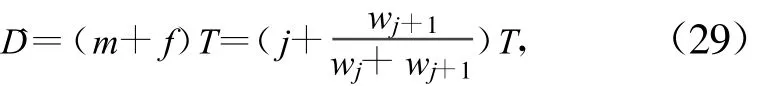
或根据式(28),时延估计为:
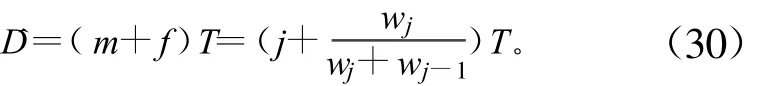
当f<0.5时,由式(23)可以看出 wj-1<0;当f>0.5时,由式(26)可以看出 wj-1>0。所以在实际应用中,当 wj-1<0时,用式(29)估计时延;当wj-1>0时,用式(30)估计时延。
3 仿真验证
仿真参数如下:仿真信号调制样式为2PSK,调制码元信号为Matlab7.0随机产生的0、1序列,码元速率fk=5 kbit/s。根据通信原理2PSK调制有关理论,已调信号第一零点带宽Bs=10 kHz。已调信号载频fc=20 kHz,也就是一个码元宽度内4个载波周期。采样频率 fs=10fc,时差D=3.4 T(T为采样间隔,T=1/fs);高斯带限白噪声中心频率fi=20 kHz,带宽。在不同信噪比下对3种自适应时延估计方法各做50次仿真试验,图2和图3为估计均值和方差结果比较。可以看到在小信噪比时,本节提出的P-LMSTDE方法时延估计方差小于其他2种自适应时延估计方法;3种方法的估计均值基本相同。

图2 不同信噪比下3种自应时延估计方法的估计均值
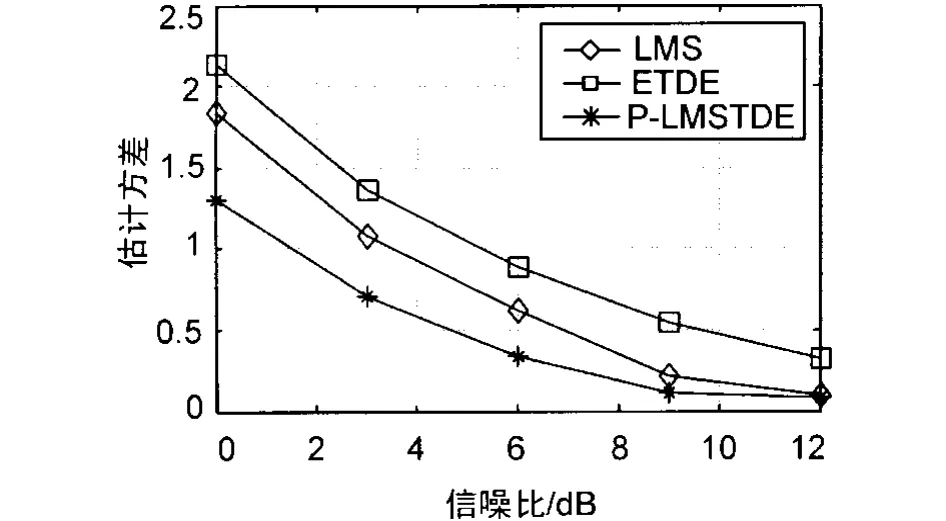
图3 不同信噪比下3种自应时延估计方法的估计方差
4 结束语
时差定位应用中,需要对侦收的来波信号进行离散采样后估计时差。来波信号到达2个传感器的时差D通常不是采样间隔T的整数倍。参数途径时延估计方法可以直接估计非整数倍采样间隔的时差,且不需要插值运算。把参数途径时延估计方法推广到应用LMS算法来实现,通过理论推导给出了时延估计的方法和步骤。计算机仿真验证了新方法的有效性和正确性。
[1]BECKER K.An efficient method of passive emitter location[J].IEEETrans on AES,1992,28(4):1091-1104.
[2]SO H C,CHING P C.Performance analysis of ETDGE-an efficient and unbiased TDOA estimator[J].IEE Proc Rardar,Sonar and Navig,1998,45(6):325-330.
[3]杨林.TDOA被动定位方法及精度分析[J].国防科技大学学报,1998,20(2):49-53.
[4]NIKIAS C L.Time delay estimation in unknown gaussian spatially correlated noise[J].IEEE Trans on ASSP,1988,36(11):1706-1714.
[5]WU YONG.LEYMIN A R.Time delay estimation in unknown spatially uncorrelatedgaussian noise using high-order statistics[C]∥International Conference Proceedings on ASSP,1999:2813-2816.
[6]YOUN D H.On using the L MS algorithm for time delay estimation[J].IEEE Trans on ASSP,1982,30(5):789-801.
[7]WANG JIN-LIN.Application of adaptive filter in time delay estimation generalized interpolation method[J].Journal of Acoustics,1992,17(3):208-216.
[8]HUANG JIA-REN.An interpolation algorithm ofthe correlation peak for time delay estimation[J].Applied Acoustics,1996,15(6):33-36.
[9]CHAN Y T.A parameter estimation approach to time-delay estimation and signal detection[J].IEEE Trans on ASSP,1980,28(1):8-15.

