FSK信号非相干解调的数字实现

王 伟,张 靖,王伟伟

(1.通信网信息传输与分发技术国防科技重点实验室,河北石家庄050081;2.石家庄市动力机械厂,河北石家庄052165)

0 引言

移频键控(FSK)信号的解调通常可分为相干解调和非相干解调2大类。其中相干解调方式需要提取载波频率和相位信息进行解调,其抗噪声性能优于非相干解调,但是由于需要进行载波恢复而使得其设备比非相干解调复杂,并且难以在短时间内对接收信号的相干载波进行准确的估计和跟踪。非相干解调不需要载波同步,并且同相干检测相比,其信噪比损失不大,适合于存在多径时延和相位起伏的突发通信模式中。

FSK信号的非相干解调的传统方法是对输入的中频信号采用带通滤波后,再进行包络检波,比较每个频点检波能量来实现解调。但是简单的带通滤波器通常不能满足实际解调的需要,因为调频信号在调制速率较高的情况下,每个码元包含的载波周期数较少,信号呈现窄带特性,使带通滤波器很难对不同载波的信号作出灵敏的反映。因此需要采用高选择性梳齿滤波器进行非相干包络检波,同时采用前向提取定时脉冲的检测方式,使调频解调器易于采用大规模集成电路实现,以下将以2FSK为例介绍全数字调频解调器的实现原理。

1 解调器设计

在数字接收机的设计中,移频键控信号经过收信机放大和变频后,成为一个幅度稳定的低中频信号。根据中频采样接收机的结构,A/D变换器直接对低中频信号采样,采样后由DSP芯片完成移频键控的全数字解调。全数字解调器主要完成信号的包络检波、定时提取和判决输出,因此解调器由数字下变频器、包络检波器、定时恢复单元等部分组成,整个解调器工作原理框图如图1所示。

全数字调频解调器首先把低中频模拟信号进行A/D变换,在数字域上进行解调处理,数字信号处理采用FPGA来实现。

调频信号通过变换频率来代表基带信息,因此通过检测信号包络,比较每个频点的能量大小就可以恢复出原始信息。设2个频率点为 f1、f2,A/D采入的信号分别由2个频率为f1、f2的NCO混频到零频,经过低通滤波滤除倍频项和带外噪声后,I、Q两支路进行平方相加,计算每一个支路的能量,在比特定时脉冲的控制下,比较2路能量就可以恢复出基带信息。

图1 全数字2FSK解调原理框图

2 包络检波的IIR实现

数字包络检波器,可分为中频检波器和零频包络检波。在中频进行包络检波,需要Q值极高的带通滤波器,硬件实现复杂;利用调制信号的等效低通表示,可以采用零频包络检波,其包络检波仅需要低通滤波器。因此,方案采取零频包络检波方式,下面考虑低通滤波器的设计实现。

FIR滤波器传输函数的极点固定在原点,所以只能用较高的节数达到高的选择性,对于同样的滤波器设计指标,所需要的阶数可高达IIR滤波器的5到10倍,消耗硬件资源大,信号延迟也大;而IIR滤波器传输函数的极点可以位于单位圆的任何地方,以很少的阶数,或消耗很少的硬件资源就可以达到高选择性。

在IIR滤波器中,梳状谱滤波器是一种特殊形式的滤波网络,利用梳状滤波器可以实现通带宽度极窄的滤波器。因此,这里采用无限循环累积型数字梳状谱IIR滤波器实现零频包络检波。

低通型梳状滤波器的系统函数可以表示为：

相应的系统传输函数为：

幅频特性为：

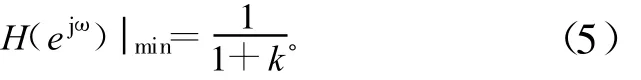
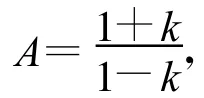
图2是梳状滤波器的幅频特性和相频特性,其中N=8,k=15/16。

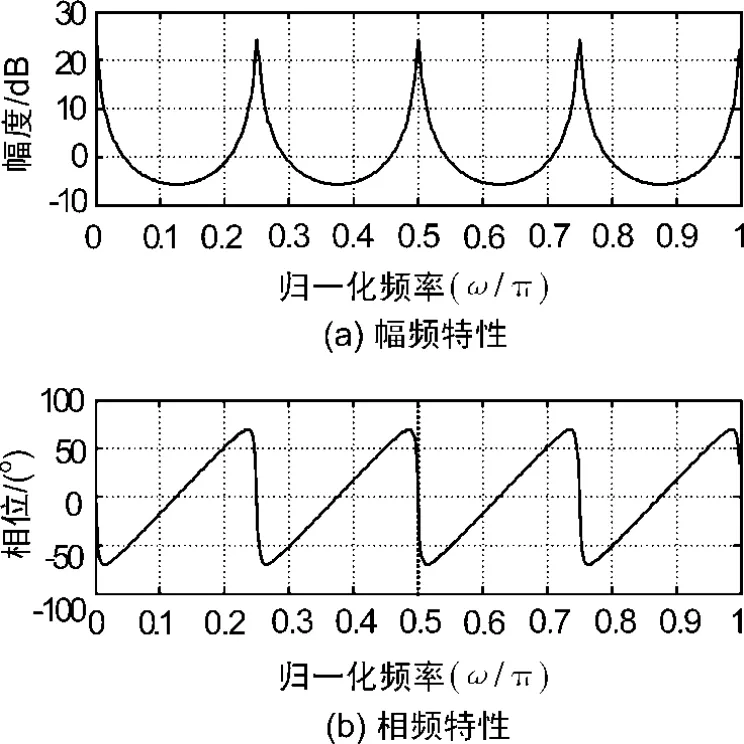
图2 低通型梳状滤波器的幅频及相频特性

由梳状滤波器的幅频、相频特性可知,除零频外,还存在若干点频通带,包络检波器只取其零频处的窄带特性,因此还需要在梳状滤波器后再串接一个FIR低通滤波器,该FIR低通滤波器的选频特性要求就大为放低了。

3 定时恢复算法

定时恢复算法主要分为2类：闭环算法和开环算法。闭环算法是从数字信号中提取与码元定时信号相位相对应的误差信号,并用此误差信号去控制NCO来产生所需的码元定时信号。开环算法又称前向算法,直接从数字信号中测量定时脉冲的最佳采样时刻。

在开环算法中,有一类重要同步算法称为谱线产生定时恢复法,其方法是通过对接收到的基带信号进行非线性变换,变换后的信号频谱在符号速率处含有丰富的定时分量。通过窄带带通滤波器提取这个定时频率分量或使用锁相环跟踪该信号,最后对提取的定时信号进行适当移相,使移相后的定时脉冲位于包络信号最佳采样点,就完成符号定时恢复。本方案对谱线产生定时恢复法进行了设计实现。

2FSK信号包络检波后的每一个频点支路其实已经含有定时周期分量,为了把整个信号能量全部利用起来,可以对其中一个频点的包络固定延迟1/2符号间隔,再把2个频点包络相加。经过上述变换后的信号含有丰富的定时谱分量,采用带通滤波器滤取定时单谱分量后,再经过移相网络和过零判决器最终恢复定时信号。

白高斯噪声经过延时后与原来的输入不相关,而周期信号经过延时前后保持强相关,符号定时谱就满足这一条件。仿照低通型梳状滤波器的特性,可以采用带通型梳状滤波器实现定时信号的提取。

带通型梳状滤波器的系统函数如式(6)所示：

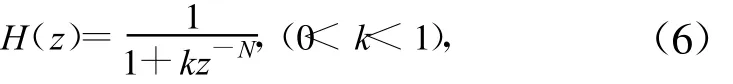
相应的系统传输函数为：

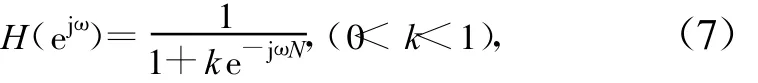
幅频特性为：

由带通型梳状滤波器相频特性图可知,相频特性 φ(ω)也是频率的周期函数,且周期为2π/N,当ω=2π(n+1/2)/N 时,φ(ω)=0,即在梳状滤波器幅频特性的极值点不引入附加相移。但是在梳状滤波器幅频特性极大值附近,引入的附加相移随频率变化的斜率是负值,其绝对值随着k的增加而急剧增大。当k值较大时,在滤波器幅频特性极大值附近的微小的频差就会带来较大的附加相移,在提同步时,表现为产生较大的定时同步相位移动,这样就会较大幅度地偏移最佳采样点,从而造成信噪比损失。因此滤波器k值的选取应在满足检测性能的前提下,尽量选小一些,以减少由于收发两端频率漂移而在收端产生的抖动。

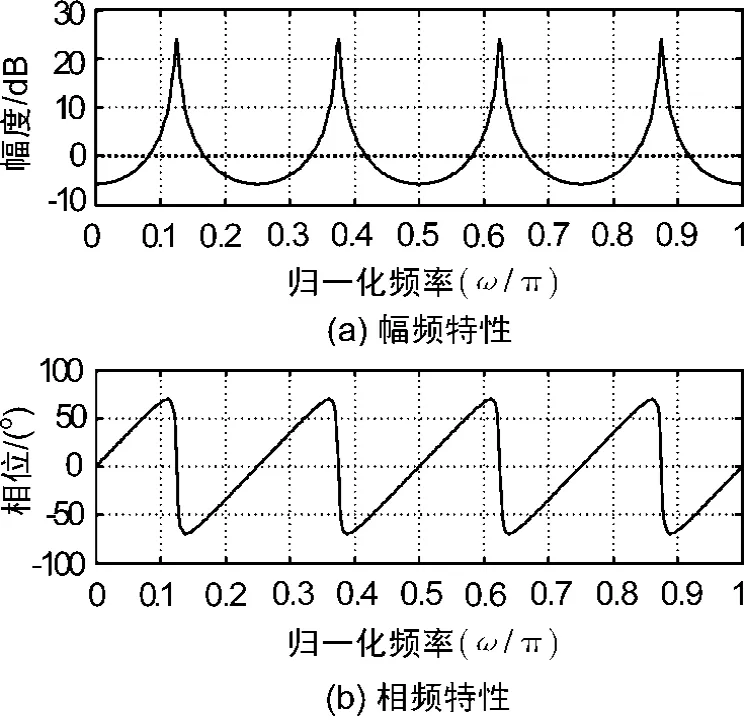
图3 带通型梳状滤波器的幅频及相频特性

带通型梳状滤波器在0～π区间内存在 N/2个梳齿,通常取频率最低的第1个梳齿作为定时提取的工作频带,其他齿峰需要级联一个FIR低通滤波器予以滤除。提取后的定时信号可以再通过数字内插滤波器进行进一步的降低抖动。

在定时抖动和抗噪声性能要求严格的场合,还可以级联IIR陷波滤波器进一步抑制梳齿滤波器的用梳齿。数字陷波器的系统函数如下：

式中,A(z)为全通滤波器,全通滤波器取二阶时,传输函数可表示为[1]：

式中：

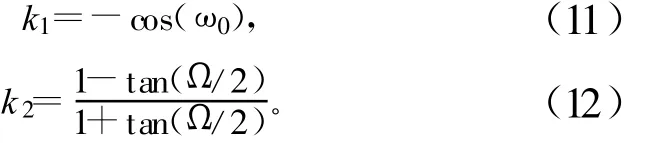
式中,ω0为陷波频率,Ω为衰减3 dB的陷波带宽。全通滤波器可以由高效的格型结构来实现,格型结构滤波器具有模块结构、对参数量化效应不敏感等优点。

式(11)和式(12)表明,该滤波器的陷波频率 ω0和3 dB衰减带宽Ω可以独立调整,互不影响。级联多个这种形式的数字陷波器可以有效消除梳状滤波器的无用梳齿。格型结构的二阶全通滤波器的实现如图4所示。

图4 二阶全通滤波器的格型实现结构

4 结束语

移频键控调制方式在中低速数字传输中,特别是在衰落信道中传输数据时,有着广泛的应用。包络检波方式可以避免相干载波的提取,在快速衰落信道和突发通信模式中,具有一定的优势。采用无限循环累积型数字梳状滤波器来实现调频信号的包络检波和定时提取,正是利用了IIR滤波器的高选择性,简化了硬件实现的复杂度。为进一步提高梳齿滤波器的选择性,还可以在梳齿滤波器后级联FIR低通滤波器和陷波器。该移频键控非相干解调方案已用于多个实际工程,实际工作状况良好,证明了该方案的可行性和有效性。

[1]REGALIA P A,MITRA S K,VAIDYANATHAN P P.The digital all-pass filter：A versatile signal processing building block[J].IEEE,1988,76：19-37.

[2]OEI S C,TSENG C C.IIR multiple notch filter design based on allpass filter[C]//IEEE TENCON-DigitalSignal Processing Applications.1996：267-272.

[3]PROAKIS J G.数字通信(第4版)[M].北京：电子工业出版社,2003.

[4]杨绿溪.现代数字信号处理[M].北京：科学出版社,2008.