基于最小二乘支持向量机的振动切削力软测量模型及其应用

张海鹰，廖建勇

(湖南城市学院 建筑与城市规划学院，湖南 益阳，413000)

随着科学技术和工业生产的发展，对各种精密机械零件的加工精度和表面质量的要求越来越高[1-2]。而传统的切削加工效率很低，难以保证不锈钢、耐热钢及钛合金等各种难加工材料高精度技术要求，为此，出现了许多新的切、磨、削加工方法，而振动切削就是其中之一[1-6]。由于振动切削力随着刀具的磨损、破损及振动等现象发生明显变化，粗加工和难加工材料加工时的振动切削力是影响振动切削过程的主要因素之一[7-11]。因此，准确地测量振动切削力，并利用它对振动切削状态进行在线预报和监控非常重要。然而，由于振动切削材料本身具有复杂性和多变性，人们对振动切削加工的微观机理的解释尚缺乏科学的定量描述，对材料的振动切削工程问题求解较困难，这对材料的振动切削理论的研究带来了难度。软测量技术(Soft-sensing technique, SST)[12]以及支持向量机(Support vector machine, SVM)技术[13-15]的飞速发展，为振动切削力软测量的实现提供了一条新思路。为此，本文作者提出1种利用多个振动切削特征参数作为辅助变量，基于最小二乘支持向量机(Least squares support vector machine, LS-SVM)的软测量技术测量振动切削力的新方法。

1 数控车床振动切削实验

1.1 数控车床振动切削实验系统

在CK6136型数控车床上设计如图1所示的同机床水平回转刀架相配套的振动实验系统。

微驱动刀架通过过渡安装板装夹到机床回转刀架上；型号为CN61M/HPV的压电陶瓷电源的输出线采用单股屏蔽电缆与微驱动刀架上对应正负极相连；压电陶瓷电源通过 25芯电缆和插在计算机内的接口相连；自行设计的车刀安装到微驱动刀架上，通过计算机来控制压电陶瓷电源的输出。

在车刀上粘贴合适的应变片，通过导线连接到电桥盒上形成电桥，通过TST3829型动静态电阻应变仪将测量信号放大，并通过示波器计录输出信号，或由A/D转换板将TST3829型动静态电阻应变仪与计算机相连接。

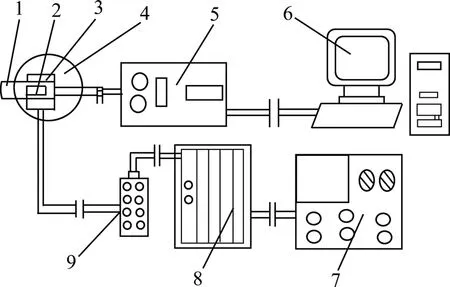
图1 数控车床振动实验系统Fig.1 Vibration cutting experiment system of numerically controlled lathe

1.2 车床振动车削实验条件

待加工试件材料为经正火处理的45号钢，直径×高为50 mm×300 mm。CK6136型数控车床的主轴转速n为 150～2 000 r/min，振动频率f为 50～250 Hz，振幅A为 8～12 μm；振动切削速度v为 3.0～100.0 m/min，进给量f1为 0.04～0.25 mm/r，切削深度ap为 0.02～3.00 mm。刀具的主前角γ= -5°～15°，后角α0=6°，刃倾角λs=0°，主偏角Kr=75°。程序运行前，将刀具调整到某点定位。此零件加工分3次进刀：第1次进刀1.00 mm，第2次进刀1.00 mm，第3次进刀0.97 mm。加工前尺寸为加工后尺寸为

待加工试件加工时的主切削力由 QJ44型电桥盒和应变片组成的测力系统进行测量。由于应变片的机械应变为10-3～10-6，通过QJ44型电桥盒测量电阻变化，并将此信号经过应变仪放大后输出到示波器上，然后，根据标定数据对主切削力进行计算。

1.3 振动车削实验结果

改变振动频率f、振幅A、振动切削速度v、进给量f1，在车床振动切削过程读取25组(包括振动切削力F1、振幅A、振动频率f、进给量f1与切削速度v)信号数据，其部分结果如表1所示。

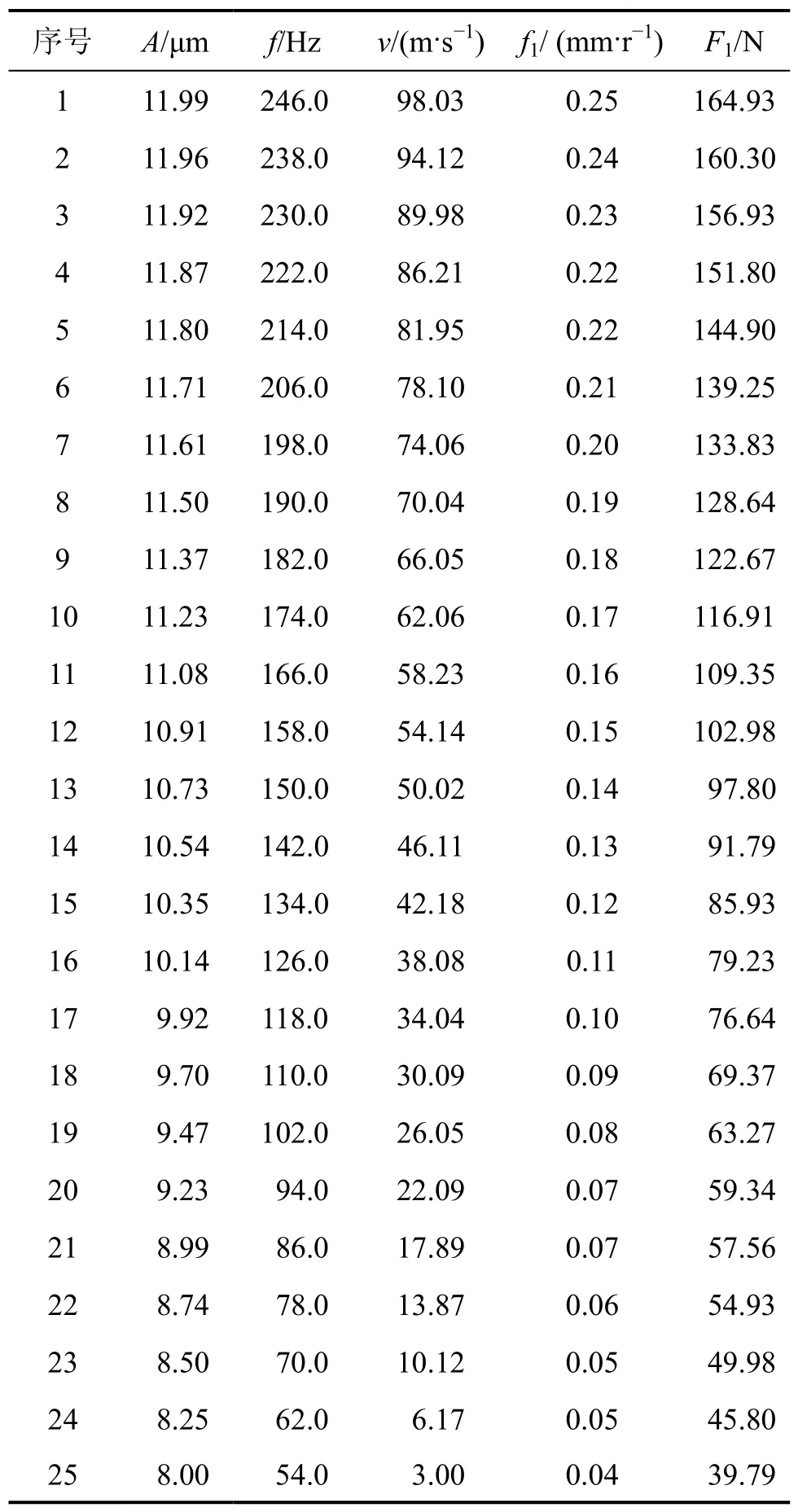
表1 振动切削实验测量值Table 1 Measurement values of vibration cutting experiment

2 振动切削力软测量模型

在现有技术条件下，车床振动切削力难以直接测量或不易快速在线测量，可通过控制其他可测变量或者采用其他数据处理方式间接地保证振动切削质量要求。因此，振动切削力(即主导变量)的软测量可利用振幅A、振动频率f、进给量f1与切削速度v这4个振动切削特征参数(即可测变量)作为辅助变量(常称为二次变量)，然后，借助支持向量机构造某种以可测变量为输入、主导变量为输出的数学模型，最后，利用计算机软件实现主导变量的估计与控制。振动切削力软测量器估计值可作为控制系统的被控变量或反映过程特征的工艺参数，为振动切削过程优化控制与决策提供重要信息。

振动切削力软测量模型构建的总体思路是：对振动切削所有工况通过1个如图2所示的最小二乘支持向量机建立1种非线形映射关系，将环境状况的可调参数作为支持向量机的输入参数，将振动切削力作为最小二乘支持向量机的输出结果。

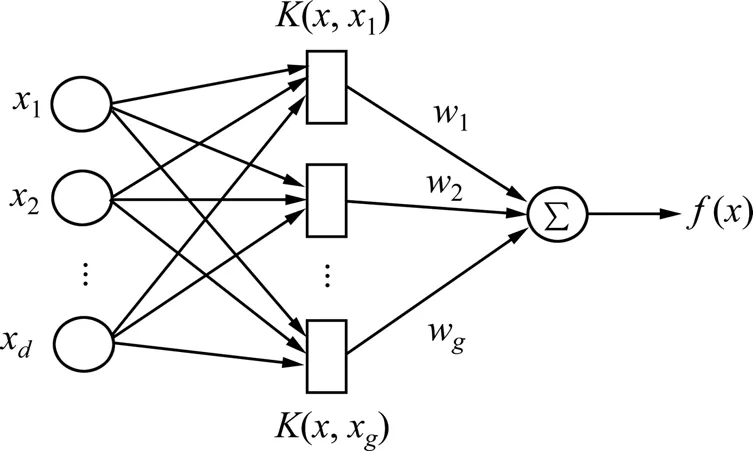
图2 支持向量机网络结构Fig.2 Network structure of support vector machine

该最小二乘支持向量机的网络结构有3层：输入层节点数为输入向量的维数d，输入为x1,x2, …,xd；隐层节点个数即为支持向量的个数，且每一个支持向量对应于1个隐层节点；输出节点个数为1，输出为f(x)。在网络权值方面，输入层与隐层之间的网络连接权值为1，隐层与输出层之间的网络连接权值为wi。

将振动切削过程振幅A(视为x1)、振动频率f(视为x2)、进给量f1(视为x3)与切削速度v(视为x4)作为最小二乘支持向量机的输入参数，振动切削力F作为目标输出量，即

在振动切削过程中必定存在噪声，通常是高斯噪声，而且将时刻影响着系统的性能，而标准的 SVM算法抗噪声能力较弱。另外，标准 SVM 算法的速度不依赖于输入空间的维数，而依赖于样本数据的个数，样本数据越大，求解相应的二次规划问题越复杂，计算速度越慢，花费的时间越长。LS-SVM 是 Suykens和Vandewalb提出的最小二乘支持向量机，优化指标采用了平方项，只有等式约束，而没有不等式约束，简化了计算的复杂性，可较好地解决此类问题。

LS-SVM在优化目标中选取了与标准 SVM算法不同的损失函数，以误差的二次平方项代替不灵敏损失函数作为损失函数。优化问题在标准 SVM 的基础上进行改进：

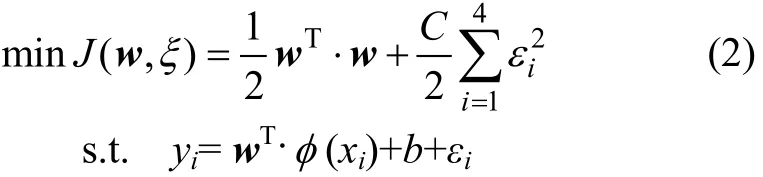
式中：εi＞0；i=1，2，3，4；C为可调参数；b为偏差量；ξ∈R，为误差变量；φ(xi)：Rn→Rnh为核空间映射函数；w∈Rnh，为权矢量。

相应的拉格朗日函数为：

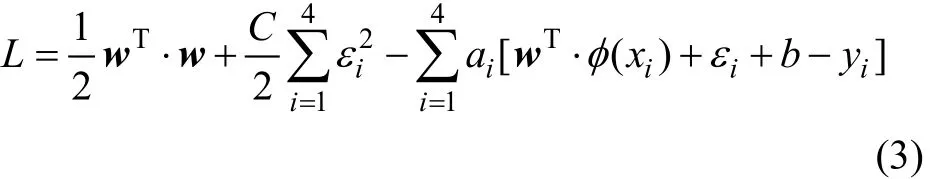
其中：i=1, 2, 3, 4。化简式(3)，消去ξ和w，则可将单工况多次映射最小二乘支持向量机优化问题转化为求解线性方程：

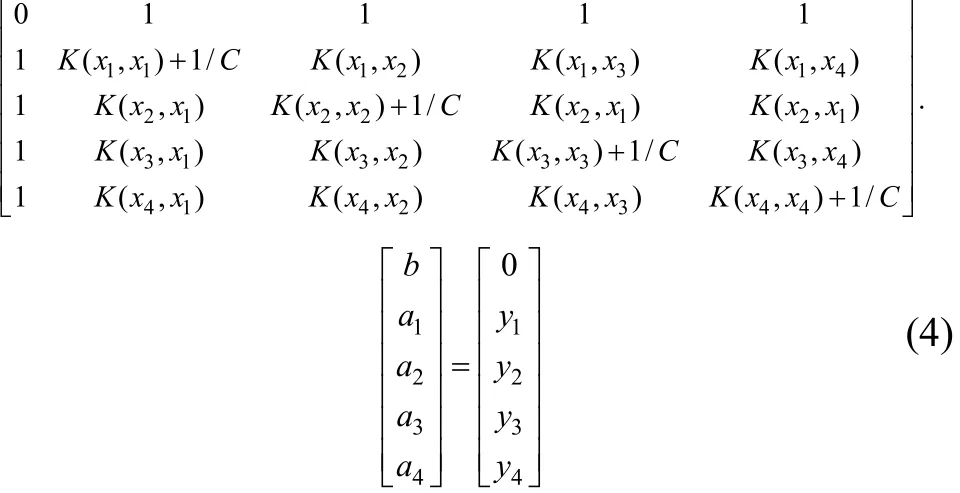
式中：核函数k(xi,xj)=φ(xi)·φ(xj)；i=1，2，3，4；j=1，2，3，4；核函数取高斯核函数(径向基核函数)；k(xi,xj)=

振动切削力软测量模型为：

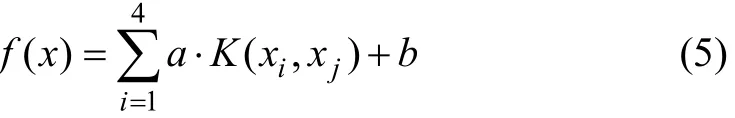
其中：i=1，2，3，4；j=1，2，3，4。应用最小二乘法进行振动切削力软测量模型辨识时，正则化参数C和核参数σ的选择是一个重要问题。用网格搜索法先选择参数对(C，σ)，然后，用交叉验证法对目标函数(如均方差最小)进行寻优，直至找到最佳的参数对，交叉验证的精度最高，并且能够避免过拟合问题。选择最佳参数对的过程为：

(1)确定合适的正则化参数集和核参数集。实验结果表明：按照指数增长方式生成2种参数集是一种有效的方法，例如，C=2-2，2-0，…，210，…；σ=2-8，2-6，…，2-2，20，…。网格搜索简单、直接，因为每一个参数对(C，σ)是独立的，可以并行地进行网格搜索。

(2)参数对进行交叉验证。应用网格搜索法选择1个参数对(C，σ)进行交叉验证，其交叉验证步骤如下：

① 把样本集G分为I组验证集，即{G1，G2，…，Gi，…，GI}；

② 把任意的I-1组作为训练集，剩余的1组作为验证集；

③ 选择不同的验证集，重复S次，其泛化性能可通过下式评价：

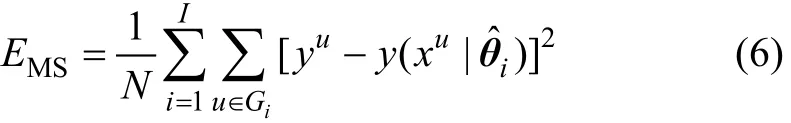
式中：Gi为第i组验证集；yu为验证集的第u个样本值；为用G-Gi作为训练样本时得到的参数向量，即式(5)中的为LS-SVM的输出。

④ 循环选择参数对进行交叉验证，计算每个参数对的EMS，当EMS最小时，该参数对(C，σ)是最佳的，网格搜索停止；否则，返回(1)，继续分组并进行交叉验证。

3 振动切削力软测量模型应用

3.1 振动切削力软测量仿真分析

取表1中前15组数据对振动切削力软测量模型进行训练，并用后10组数据对训练后的模型进行检验。振动切削力软测量值与实际测量值在训练集与测试集中的对比及相应的误差曲线分别如图3～6所示。

从图3～6可以看出：基于最小二乘支持向量机的振动切削力软测量值的建模精度较高，泛化能力较强，所得的振动切削力最大训练误差为3.0 N(此时，相对误差约为1.87%)，振动切削力最大测试误差为1.47 N(此时，相对误差约为1.95%)。

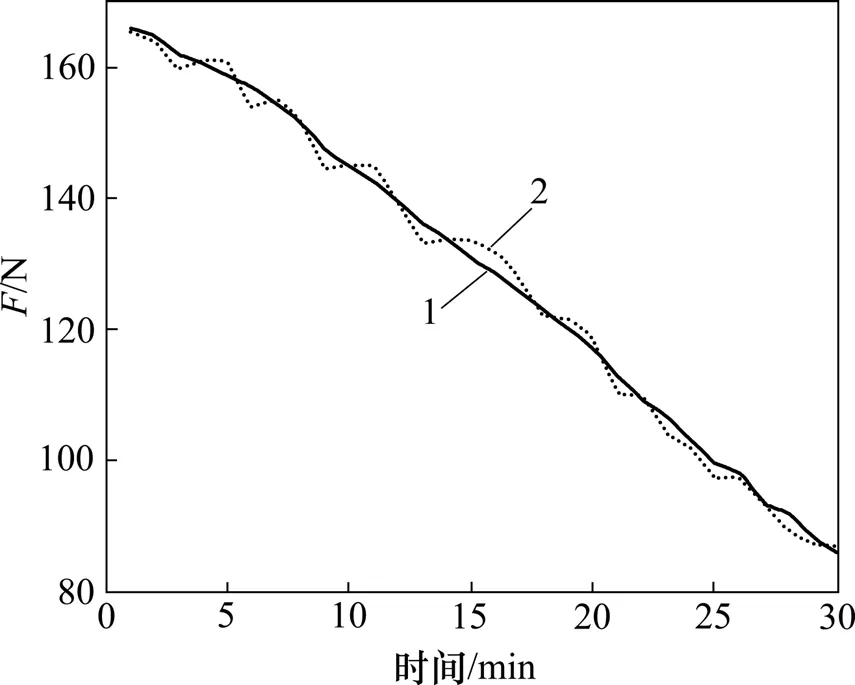
图3 训练集的振动切削力软测量结果Fig.3 Vibration cutting force of soft-sensing based on training set

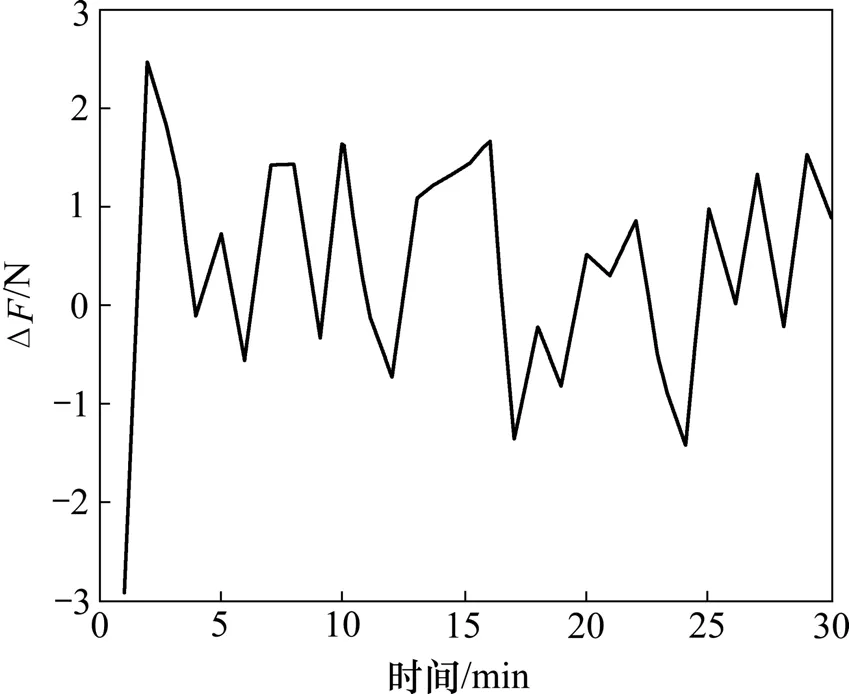
图4 训练集的振动切削力软测量结果误差ΔF曲线Fig.4 Error of vibration cutting force of soft-sensing based on training set

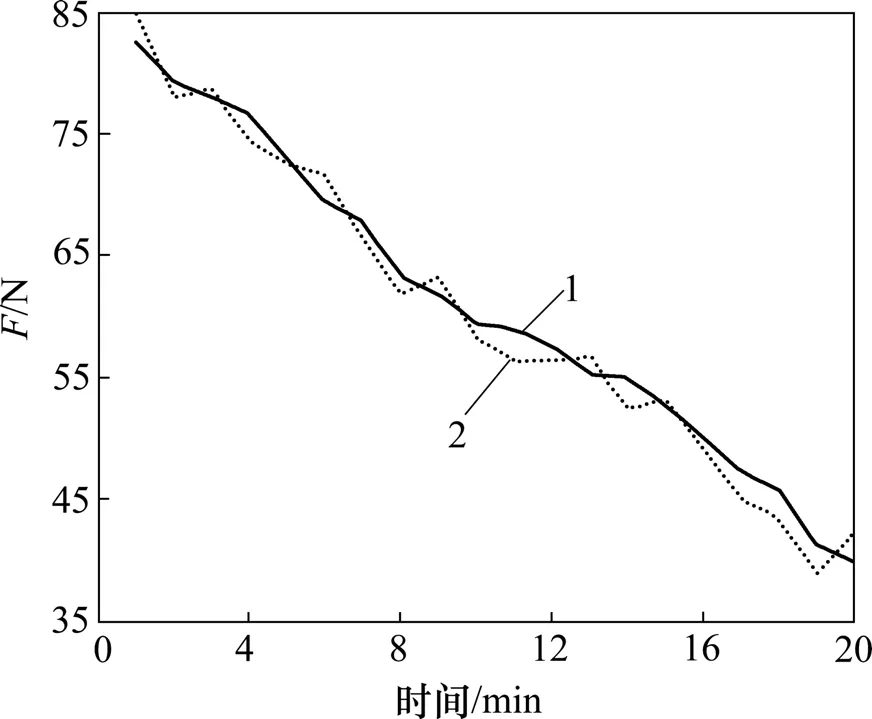
图5 测试集振动切削力的软测量结果Fig.5 Vibration cutting force of soft-sensing based on test set

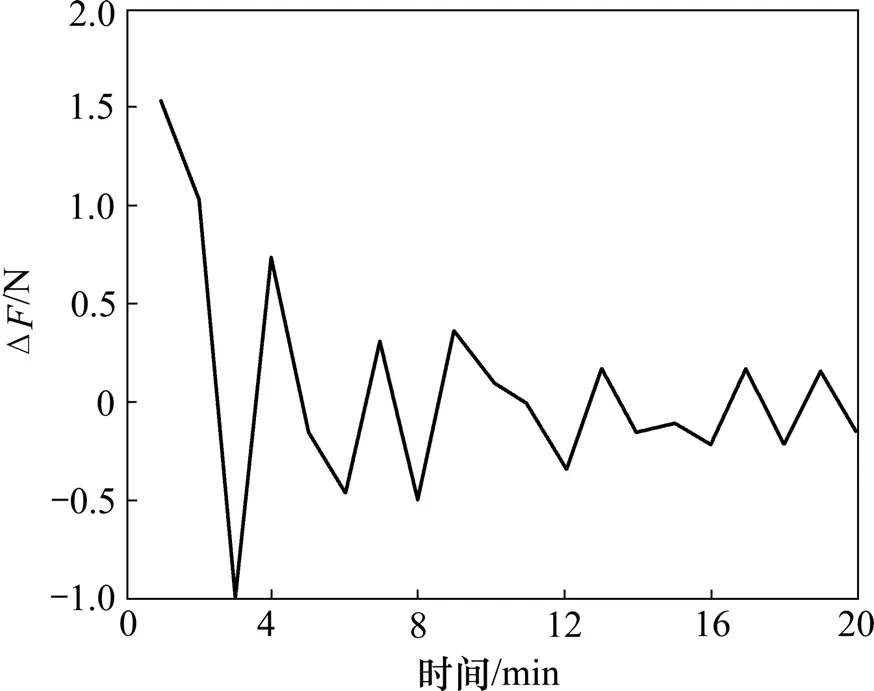
图6 测试集的软振动切削力测量误差ΔF曲线Fig.6 Vibration cutting force error of soft-sensing data from test set

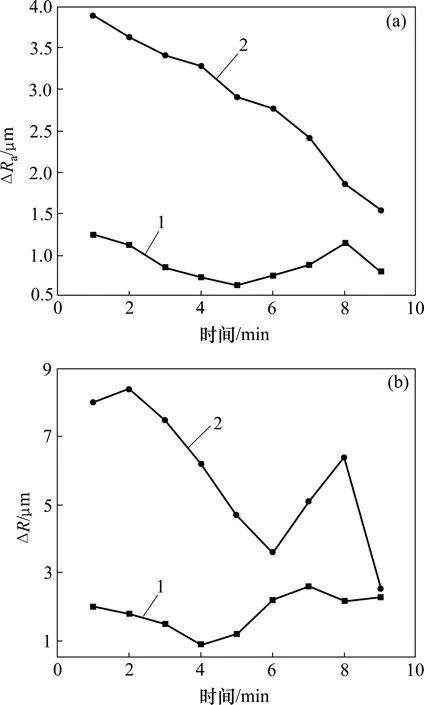
图7 振动切削阻力软测量应用效果Fig.7 Application effects on soft-sensing model of vibration cutting force

3.2 振动切削力软测量实际应用分析

采用前面的车床振动车削实验系统，对比分析利用振动切削力软测量模型测量振动切削力与不测量振动切削力时所得到的切削加工工件的加工精度。加工工件圆度误差采用凸轮轴检查仪进行测量，其表面粗糙度采用SV-C3000超级表面粗糙度轮廓仪进行测量，在加工工件上随意选取27个测试点，取其中9个最大的数据进行对比分析，结果如图7所示。从图7可知：对振动切削力进行软测量的加工工件，其表面粗糙度误差为1.0～1.4 μm，不对振动切削力进行测量的加工工件表面粗糙度误差为1.5～3.9 μm，表面粗糙度平均误差降低50%以上；对振动切削力进行软测量的加工工件圆度误差为1.1～2.4 μm，不对振动切削力进行测量的加工工件，其圆度误差为2.6～8.4 μm，圆度平均误差降低70%以上。可见：采用软测量模型对振动切削力进行软测量后，工件加工精度得到较大提高。

4 结论

(1)利用数控车床振动切削实验系统对振动切削力F1、振幅A、振动频率f、进给量f1与切削速度v进行了数据采集，并将其作为最小二乘支持向量机的输入参数。

(2)基于最小二乘支持向量机的振动切削力软测量值的建模精度较高，泛化能力较强，所得的振动切削力最大训练为3.0 N(此时，相对误差约为1.87%)，振动切削力最大测试误差为1.47 N(此时，相对误差约为1.95%)。

(3)对振动切削力进行软测量后，加工工件表面粗糙度误差和圆度误差与不对振动切削力进行测量的加工工件表面粗糙度误差和圆度误差相比，表面粗糙度平均误差降低50%以上，圆度平均误差降低70%以上，其加工精度得到较大提高。

[1] Masahiko J, Masao M. Development of a practical ultrasonic vibration cutting tool system[J]. Journal of Materials Processing Technology, 2001, 113(1/3): 342-347.

[2] Chandra Nath, Rahman M. Effect of machining parameters inultrasonic vibration cutting[J]. International Journal of Machine Tools and Manufacture, 2008, 48(9): 965-974.

[3] Xiao M, Karube S, Soutome T, et al. Analysis of chatter suppression in vibration cutting[J]. International Journal of Machine Tools and Manufacture, 2002, 42(15): 1677-1685.

[4] Shamoto E, Suzuki N, Hino R. Analysis of 3D elliptical vibration cutting with thin shear plane model[J]. CIRP Annals-Manufacturing Technology, 2008, 57(1): 57-60.

[5] Harada Kei, Sasahara Hiroyuki. Effect of dynamic response and displacement/stress amplitude on ultrasonic vibration cutting[J].Journal of Materials Processing Technology, 2009, 209(9):4490-4495.

[6] Shu K, Wataru H, Tatsuo S, et al. The non-linear phenomena in vibration cutting system: The establishment of dynamic model[J].International Journal of Non-linear Mechanics, 2002, 37(3):541-564.

[7] Kim J S, Lee B H. An analytical model of dynamic cutting forces in chatter vibration[J]. International Journal of Machine Tools and Manufacture, 1991, 31(3): 371-381.

[8] Rincon D M, Ulsoy A G., Kaftanoĝlu Bilgin. Effects of drill vibrations on cutting forces and torque[J]. CIRP Annals-Manufacturing Technology, 1994, 43(1): 59-62.

[9] Liu C S, Zhao B, Gao G F, et al. Research on the characteristics of the cutting force in the vibration cutting of a particle-reinforced metal matrix composites SiCp/Al[J]. Journal of Materials Processing Technology, 2002, 129(1/3): 196-199.

[10] Chandra N, Mustafizur R, Soon N K. Machinability study of tungsten carbide using PCD tools under ultrasonic elliptical vibration cutting[J]. International Journal of Machine Tools and Manufacture, 2009, 49(14): 1089-1095.

[11] Risbood K A, Dixit U S, Sahasrabudhe A D. Prediction of surface roughness and dimensional deviation by measuring cutting forces and vibrations in turning process[J]. Journal of Materials Processing Technology, 2003, 132(1/3): 203-214.

[12] Willis M J. Artificial neural networks in process engineering[J].IEE Proceedings-D, 1991, 138(3): 256-266.

[13] Vapnik V. The nature of statistical learning theory[M]. New York:Springer, 1999: 15-26.

[14] Gu Y I, Weston J, Barnhill S. Gene selection for cancer classification using support vector machines[J]. Machine Learning, 2002, 46: 389-422.

[15] Vapnik V. Statistical learning theory[M]. New York: Wiley, 1998:30-50.