结构优化理论在预应力混凝土连续梁桥配束中的应用
王文清,侯广伟
(1.安徽建筑工业学院,合肥 230601;2.西安铁路局 总工程师室,西安 710054)
预应力混凝土连续梁桥以结构受力性能好、变形小、伸缩缝少、行车平顺舒适、造型简洁美观、养护工程量小、抗震能力强及施工方法成熟等特点,在桥梁工程中得到广泛的应用。在预应力混凝土连续梁桥的结构计算中,确定预应力钢束(筋)的数量与位置,使结构在施工与使用阶段处于合理的受力状态是一项重要的内容。传统的配束方法是:首先按照正常使用极限状态的应力要求以及按承载能力极限状态的强度要求预估预应力钢束的数量,然后根据预应力钢束的预估数量进行预应力钢束的布置。由于结构的次内力与预应力钢束的数量和布置有关,而且结构施工方法转换体系的顺序对结构次内力的影响也很大,因此预估的预应力钢束的数量是非常粗略的,而且配置的预应力钢束又导致内力重分配,需再调整。有时结构尺寸不符合要求,亦需要调整。此过程重复几次,直到满足规范要求。因此,预应力混凝土连续梁桥的配束是一项十分繁琐的工作。
土建结构优化设计是一门土建工程与运筹学交叉的学科,它的出现使设计者从被动的分析、校核而进入主动的设计,这是结构设计上的一次飞跃。结构优化设计理论已经成功地应用于确定斜拉桥的合理成桥状态,如弯曲能量最小法(以结构的弯曲应变能作为目标函数)、用索量最小法(以索力乘以索长累计值作为目标函数),这些方法属于线性规划和非线性规划问题。
在预应力混凝土连续梁桥设计中,在满足连续梁桥各控制断面应力的条件下,使预应力钢筋数量达到最小时的配束设计方案是最经济的。因此以钢束用量最小为目标函数,采用优化设计方法进行预应力混凝土连续梁桥的配束设计是合理的。
1 钢束用量最小法的基本原理和计算步骤
1.1 基本原理
在恒载、汽车荷载、温度变化、基础沉降等作用下,计算连续梁桥各控制截面的应力向量和其中{σ}为按照作用(或荷载)的标准值组max合得到的各控制截面最大应力向量(压应力为正,拉应力为负,以下同),为按照作用(或荷载)的短期组合得到的各控制截面最小应力向量,为按照作用(或荷载)的长期组合得到的各控制截面最小应力向量。
对各预应力钢束施加单位张拉力,按施工过程求得预应力钢束对各截面的应力的影响矩阵[C]。
根据桥涵设计规范,使用阶段预应力混凝土受弯构件在正截面混凝土的压应力和拉应力均不得超过规范规定的限值。上述限值构成了优化计算模型的约束条件。
1)混凝土压应力限值
对全预应力混凝土构件和A类预应力混凝土构件,{σmax}+[C]{Ti}其结果均≤0.5fck(fck混凝土标准抗压强度,Ti为第i根钢束的张拉力)。
2)混凝土拉应力限值
当然,设计者也可根据桥梁使用耐久性的要求,提出混凝土应力(包括压应力、拉应力、主压应力、主拉应力等)的限制值。显而易见,只需改变优化计算模型的约束条件,即可达到上述目的。
1.2 计算步骤
1)拟定结构尺寸和预应力钢束的位置;
2)在恒载、活载、温度变化、支座沉降等作用下,当不考虑混凝土收缩徐变时,按照实际施工步骤对全桥进行结构计算,形成各控制断面的应力向量{σmax}、和
3)不考虑混凝土收缩徐变的影响,对各预应力钢束施加单位张拉力,按施工过程求得预应力钢束对各截面的应力的影响矩阵[C]。计算时,考虑了除混凝土收缩徐变影响以外的全部预应力损失;
4)求解U→min的线性规划问题,得到不考虑混凝土收缩徐变时的钢束张拉力 { T0};
5)将索力转换成相应的钢束数目,将此结果带入到计算模型中重新进行计算,并考虑混凝土收缩、徐变的影响,重新形成各控制断面的应力向量 { σmax}、此时,预应力钢束考虑了包括混凝土收缩徐变影响的全部预应力损失;
6)重新求解 U→min的线性规划问题,得到考虑混凝土收缩徐变的钢束张拉力 { T1};
7)对连续梁桥的各控制断面进行应力验算;
8)重复第5)~7)步,直到整个结构满足应力条件为止。在一般情况下,2~3个循环即可达到设计要求。
2 算例
某三跨变截面预应力混凝土连续梁桥,跨径组合为(40+60+40)m,支点梁高3.3 m,跨中梁高1.6 m,如图1所示。上部结构采用双幅桥布置,主梁采用单箱双室的箱形截面,箱梁的顶板宽13.5 m,底板宽8.5 m,顶板厚22 cm,腹板厚30 cm,底板厚40~25 cm,如图2所示。箱梁采用 C50混凝土,预应力钢材采用ASTM A416-87a标准270级钢绞线,公称直径为15.24 mm,抗拉强度标准值为1 860 MPa。设计荷载为公路—Ⅰ级。主梁按照全预应力混凝土结构进行设计。本桥采用悬臂挂篮法施工。

图1 桥梁立面与截面编号(单位:cm)

图2 桥梁横断面(单位:cm)
预应力钢束的布置形式,与桥梁结构体系、受力情况、构造形式和施工方法都有密切关系。采用悬臂挂篮法施工的预应力混凝土连续梁桥的布束形式分为悬臂力筋、中跨力筋、边跨力筋和连续力筋。布置在梁顶的悬臂力筋主要承受结构的重量与施工荷载,中跨合龙段附近的下缘钢束和边跨用支架施工端部梁段的下缘钢束除了承受活载需要外,常因结构次内力在这些部位产生正弯矩而需要布置。根据以上的布束特点,拟定本桥的预应力钢束的位置,如图3~图5所示。

图3 悬臂钢束布置(单位:cm)

图4 中跨钢束布置(单位:cm)

图5 边跨钢束布置(单位:cm)
对各预应力钢束施加单位张拉力,按施工过程计算预应力钢束对各截面的应力的影响矩阵,见表2。求解U→min的线性规划问题,得到不考虑混凝土收缩徐变时的钢束张拉力,并将索力转换成相应的钢绞线数量。这时得到的各个钢束数量是不均匀的,需要对钢束数量进行均匀化处理。钢束数量的均匀化处理是通过指定优化模型中的设计变量(钢束数量)的值实现的。钢束均匀化顺序为:悬臂钢束→边跨钢束→中跨钢束。当悬臂钢束数量调整以后,边跨钢束和中跨钢束的数量随之发生变化。当边跨钢束数量调整以后,中跨钢束的数量随之发生变化,从而实现了钢束的自动调整,避免了传统方法中的顾此失彼的现象,见表3。

表1 各控制截面的应力MPa
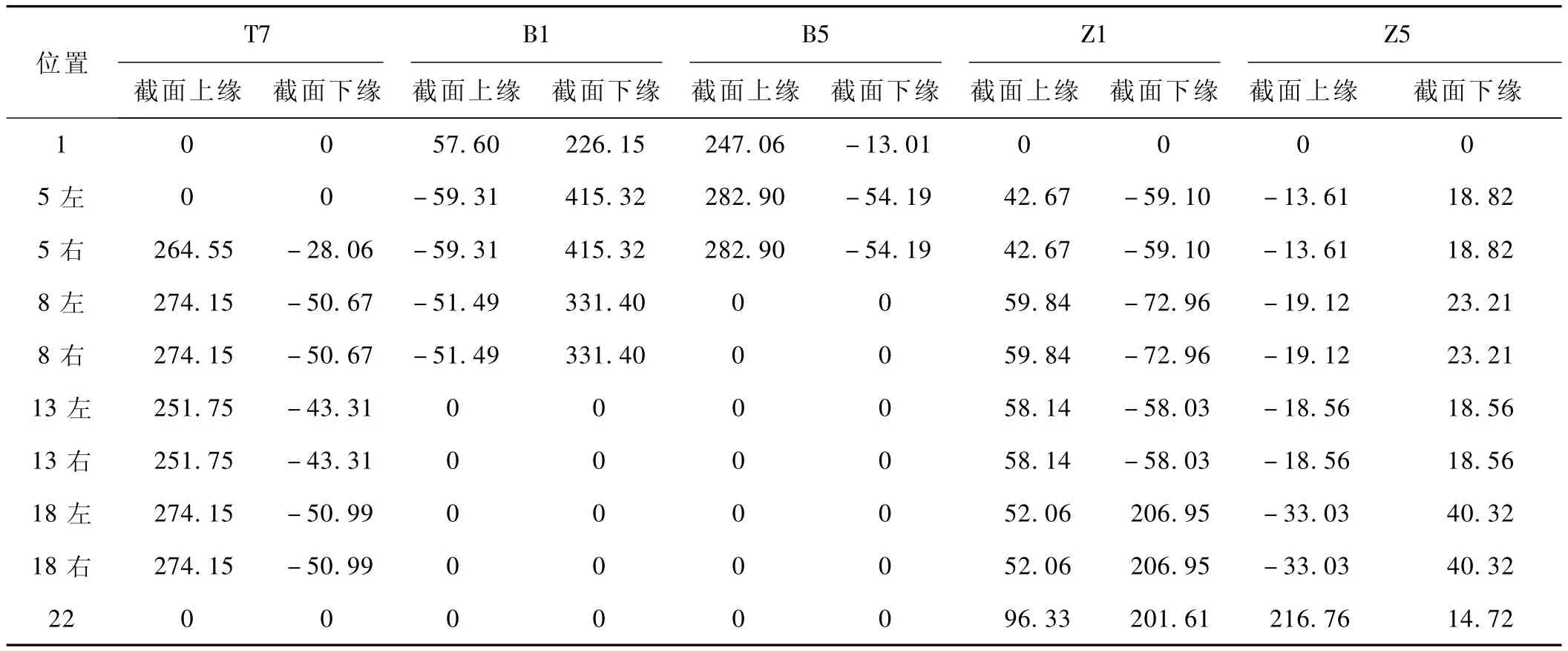
表2 预应力钢束施加单位张拉力时截面的应力 Pa/kN
将均匀化后的优化结果带入到计算模型中重新进行计算,当不考虑混凝土收缩徐变时,在恒载、汽车荷载、温度变化、基础沉降等的作用下主梁应力如图6所示。当考虑混凝土收缩徐变时,由于混凝土收缩徐变产生的次内力以及预应力钢束由于混凝土收缩徐变引起的预应力损失的影响,局部的主梁应力不满足规范要求,如图7所示。
图6 不考虑混凝土收缩徐变时的主梁最小应力(单位:MPa)

图7 考虑混凝土收缩徐变时的主梁最小应力(单位:MPa)
以上述计算结果为初始状态,并考虑混凝土收缩徐变的影响,重新形成各控制断面的应力向量以及预应力钢束对各截面的应力的影响矩阵,再次求解线性规划问题,并对各钢束数量进行均匀化处理。最终的各预应力束的钢绞线数量见表4。在各种作用或荷载的作用下,主梁应力满足规范设计要求,如图8、图9所示。

图8 在作用的短期效应组合下主梁的最小应力(单位:MPa)

图9 在作用的标准值组合下主梁的最大应力(单位:MPa)

表4 预应力钢束数量表
4 结语
基于预应力混凝土连续梁桥的配束设计的传统方法,参考确定斜拉桥合理成桥索力的“用索量最小法”,把结构优化设计理论应用于预应力混凝土连续梁桥的配束设计。通过改变优化模型的限制条件,设计者可灵活地控制混凝土的应力,并且实现钢束的自动调整,不会发生传统方法中的顾此失彼现象,而且可得出比较经济的配束结果,具有广阔的应用前景。
[1] 徐岳,王亚君,万振江.预应力混凝土连续梁桥设计[M].北京:人民交通出版社,2000.
[2] 范立础.桥梁工程(上册)[M].北京:人民交通出版社,2001.
[3] 范立础.预应力混凝土连续梁[M].北京:人民交通出版社,1988.
[4] 项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.
[5] 贺栓海.桥梁结构理论与计算方法[M].北京:人民交通出版社,2003.
[6] 张炳华,侯昶.土建结构优化设计[M].上海:同济大学出版社,1998.
[7] 江爱川.结构优化设计[M].北京:清华大学出版社,1986.[8] 中华人民共和国交通部.JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.

