高速薄壁圆柱滚子轴承拟静力学分析

苏 敏，付金辉，郑红威，邓四二

(1.洛阳LYC轴承有限公司，河南 洛阳 471039；2.河南科技大学 机电工程学院，河南 洛阳 471003)

高速薄壁圆柱滚子轴承套圈的结构变形直接影响其动力学性能和使用寿命，因此在圆柱滚子轴承设计时需要考虑套圈结构变形的影响。柔性支承的滚动轴承性能分析早就引起很多学者的关注，文献[1]在游星齿轮轴承动力学分析中，考虑了因游星齿轮支承引起的轴承套圈结构变形因素，提出了一种柔性支承的轴承力学分析方法；文献[2-3]利用有限元法对带有轴承外圈结构变形的滚动轴承性能进行了分析；文献[4]在给出简化的套圈变形表达式基础上，对柔性套圈的圆柱滚子轴承进行了性能分析。这里针对高速薄壁圆柱滚子轴承，在考虑转速对轴承套圈影响的基础上，给出薄壁套圈的结构变形解析式，利用拟静力学分析方法对轴承的动态性能进行分析。

1 数学模型

高速薄壁圆柱滚子轴承在径向载荷作用下，套圈将发生变形。套圈的变形不仅含有滚子与其之间的局部弹性接触变形，还有自身离心力引起的胀大变形和径向载荷引起的变形。在此对这些变形分别处理，并假设各个变形互不影响。

1.1 结构变形

滚子与套圈之间的局部弹性接触变形量(位置角为ψj的第j个滚子分别与内、外圈的接触变形)由滚子和内圈间接触变形量δij及滚子和外圈间接触变形量δej决定。

轴承在高速旋转时会产生很大的离心力，它所引起的胀大变形对保持架和套圈都有影响，分析时可以将套圈视为薄壁圆环。薄壁圆环在高速旋转时，由转速引起的内、外半径的增量为[5]：

(1)

(2)

式中：δc,i为圆环内径面增量；δc,e为圆环外径面增量；ρ为圆环密度；Ω为圆环旋转角速度；E为圆环弹性模量；ν为圆环泊松比;ri为圆环内半径；re为圆环外半径。

轴承内、外圈因离心力而产生的径向变形会改变径向游隙，将(1)式和(2)式分别应用于外圈内径面和内圈外径面可得到轴承径向游隙变化值。安装过盈量和内、外圈工作温度差也将影响径向游隙，为了更好地控制工况参数对离心力膨胀的影响，在轴承性能分析时，轴承径向游隙初始值输入应是考虑过盈配合和热效应影响后的值。

图1为单个线接触载荷引起的套圈椭圆变形，用Fourier级数表示为：

(3)

式中：Kk(k=0，1，2，…)为刚度系数；W为径向载荷；θ为变形位置与载荷的夹角。

图1 空心圆柱体在单一载荷下的变形

如果套圈受N个线载荷，可得其径向变形量δ(θ)为：

(4)

式中：单个接触载荷Wj与滚子的位置角ψj=(2π/N)(j-1)相对应(图2)。文中定义位于轴承径向载荷作用线上的滚子的位置角为0度，滚子编号为1，其他滚子沿逆时针方向依次类推。薄壁套圈结构变形时可将其作为薄壁圆环进行分析，根据文献[6]的假设，薄壁圆环在受到纯径向载荷作用时，切应力沿壁厚方向可视为均匀分布。文献[4]结合轴承内部受力情况，在(3)式和(4)式的基础上给出了简化的套圈变形求解公式，只需要3个刚度系数即可求出薄壁套圈的结构变形。

δ(θ)=W(K0+K1cosθ+K2cos 2θ)

(5)

式中：K0，K1，K2可按文献[4]中的方法进行计算。由(1)～(5)式可求得第j个滚子处内、外圈的结构变形量为：

Defij=0.5δc,e+δi(ψj)

(6)

Defej=0.5δc,i+δe(ψj)

(7)

式中：Defij为内圈在第j个滚子处的结构变形；Defej为外圈在第j个滚子处的结构变形。

图2 轴承在径向载荷作用下滚子与套圈载荷分布

1.2 滚子和套圈平衡方程组的建立

考虑轴承平稳运转，并忽略滚子歪斜。内圈以角速度ωi旋转，外圈以角速度ωe相对于内圈反向旋转。滚子径向受力如图3所示，Qij，Qej分别为第j个滚子与内、外圈接触载荷；F为滚子离心力；Fc1j和Fc2j为第j个滚子与保持架的摩擦力，在受载区，滚子推动保持架运动，仅存在Fc1j，在非受载区，保持架推动滚子运动，仅存在Fc2j。

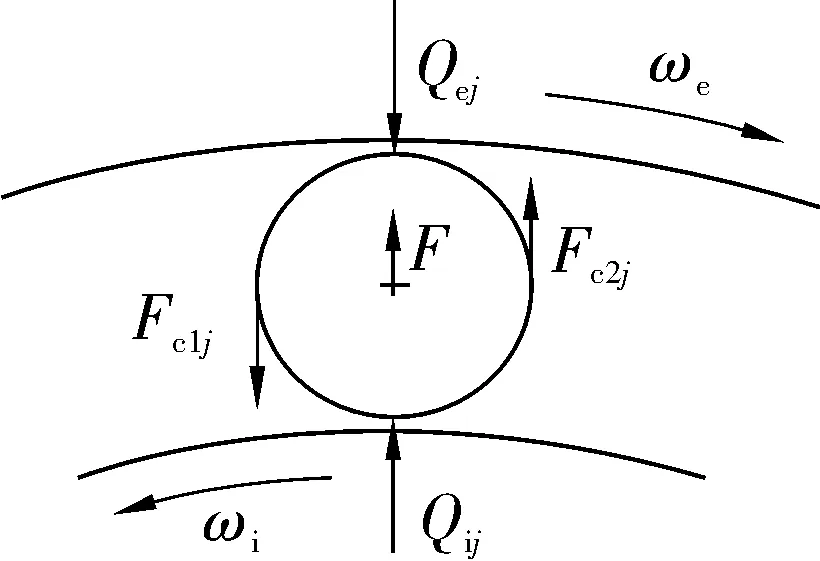
图3 滚子径向受力

滚子力平衡方程为：

Qij-Qej+F+Fc2j-Fc1j=0

(8)

轴承在径向力Fr作用下，内圈的平衡方程为：

(9)

内、外圈间的相对位移需要引入几何关系来说明，见图4。其包括滚子与内、外滚道接触区的弹流润滑油膜厚度(hij，hej)、滚子与套圈接触变形(δij，δej)、径向游隙(Gr)、结构变形(Defij，Defej)和内圈相对于外圈的径向位移(δr)。它们之间的关系可以表示为：

(Gr/2+δij+δej-hij-hej+Defij+Defej)-

δrcosψj=0

(10)

由(8)～(10)式组成的方程组中共有2N+1(N为滚子个数)个方程，由于Fc1j和Fc2j相对于Qij和Qej极小，可忽略不计，因此共有2N+1个未知数，即每个滚子与内、外圈的接触法向载荷(Qij,Qej)和内圈相对外圈的径向位移(δr)。采用BFGS数值计算法求解，可得出圆柱滚子轴承的动态特性参数。

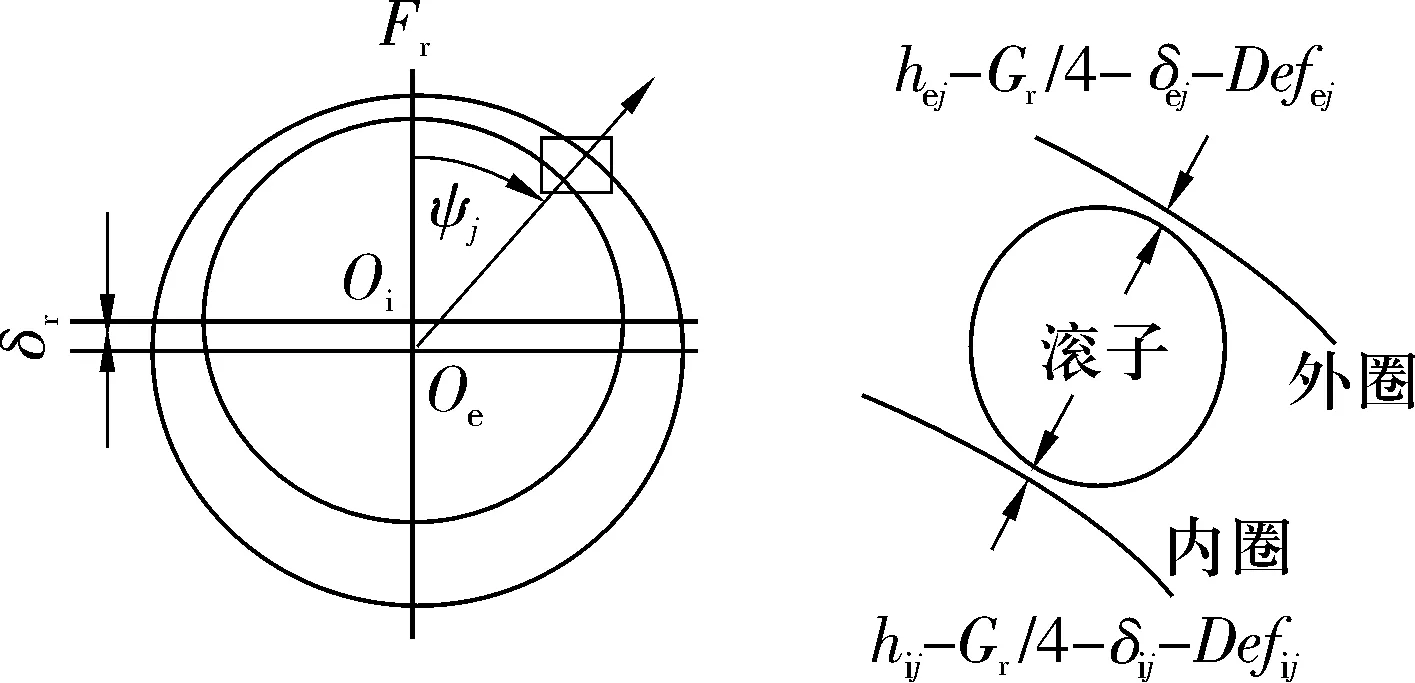
图4 几何关系

2 计算分析

以某型号高速圆柱滚子轴承为例进行分析，其相关参数见表1。该轴承在实际工作中内、外圈反向旋转，内圈转速为12 000 r/min，外圈转速为8 000 r/min。图5为轴承在Fr=4 kN时，套圈分别按刚性和柔性计算时的载荷分布。由图5可知：当套圈为刚性时，有11个滚子受载；当套圈为柔性时，受载滚子个数增加到13个。柔性套圈滚子受载区域增大，并且柔性套圈的滚子与滚道间最大接触载荷比刚性套圈的滚子与滚道间最大接触载荷要小。

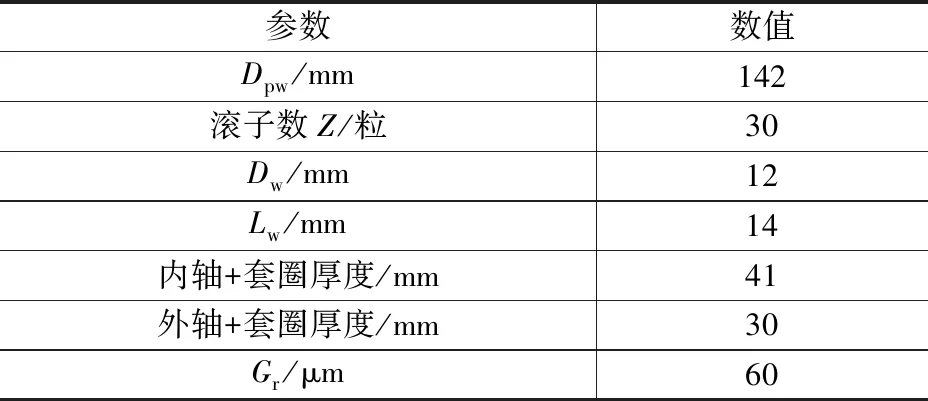
表1 圆柱滚子轴承参数

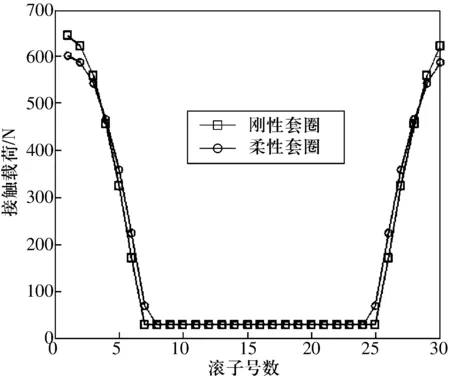
图5 滚子与内圈接触载荷分布

根据文献[7]的计算方法，图6给出了轴承在不同径向载荷下，套圈分别为柔性和刚性时轴承疲劳寿命理论计算值。由图6可知：轴承疲劳寿命随着轴承径向载荷的增大而降低，柔性套圈轴承的寿命略高于刚性套圈轴承的寿命，在载荷较大时尤为明显。这是因为载荷较大时，柔性套圈的结构变形较大，使最大接触载荷减小越明显，从而减小了最大接触载荷，提高了轴承的疲劳寿命。

图6 径向载荷与疲劳寿命的关系

图7为轴承在Fr=3 kN情况下，内圈厚度不变，外圈壁厚与外径之比为0.082～ 0.123的滚子与外滚道间接触载荷变化曲线。由图7可知：当工况相同时，随着套圈厚度变大，套圈结构变形逐渐减小。当套圈厚度与其外径之比大于0.123时，套圈变形很小，对载荷分布的影响不大。

图7 套圈厚度与接触载荷的关系(Fr=3 kN)

图8为内、外圈壁厚不变情况下，Fr=1，2，3 kN时滚子与外滚道间的接触载荷变化曲线。由图8可知：随着Fr的增大，套圈的结构变形越来越明显。当Fr很小时，套圈基本上没有变形。

3 结论

(1)柔性套圈下滚子受载区域比刚性套圈下滚子受载区域大；柔性套圈下滚子与滚道间最大接触载荷比刚性套圈下滚子与滚道间最大接触载荷小；在一定的工况下，柔性套圈有利于轴承疲劳寿命的提高。

图8 径向载荷对滚子载荷分布的影响

(2)在套圈材料不变的情况下，套圈厚度与径向载荷是影响套圈变形的主要因素。当套圈很薄或径向载荷很大时，套圈结构变形明显；当套圈很厚或径向载荷很小时，套圈结构变形较小。在工程应用中，当轴承承受较大径向载荷，套圈厚度与其外径之比又很小时，必须考虑套圈的柔性。