轴承零件圆轮廓最小二乘圆误差的Newton迭代法修正
张 慧,宋晓波,李文超,温朝杰
(洛阳轴研科技股份有限公司,河南 洛阳 471039)
在轴承套圈沟道或钢球等圆轮廓的接触式测量中,对采样点进行评定时,最小二乘圆法是目前通用的评定方法,此方法计算简便但存在一定的误差。为使评定结果更加精确,更逼近真实值,现采用Newton迭代法对最小二乘圆法评定结果进行修正。
1 圆轮廓的最小二乘圆通用算法
在轴承零件圆轮廓的实际测量过程中,得到的一系列测量点(xi,yi),按照圆的标称形式进行最小二乘圆的优化计算,可以得到圆轮廓半径和圆心的坐标[1-2]。
如图1所示,传感器实际测量出来的一系列测量点组成样本集(xi,yi),i=1,2,…,N。

图1 最小二乘圆示意图
样本集(xi,yi)中点到圆心的距离为di,则:
(1)
采用最小二乘法直接分析圆的轮廓,在对各未知参数求偏导后,无法求解,为了计算方便,可以取点(xi,yi)到圆心距离与圆半径的平方差:
(2)
(3)
(4)
(5)

k2=N∑xiyi-∑xi∑yi,
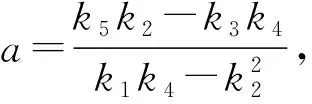

(6)
(7)
(8)
但用最小二乘圆法对圆轮廓的采样点进行评定时,不同的仪器各自存在不同的问题。
(1)对于圆度仪、圆柱度仪和沟曲率仪等仪器采用极坐标对圆轮廓进行测量评定时,采用的是采样点到圆心的距离与圆半径的平方差的平方,而不是两者差的平方,因此增加了距离与半径之和的权重,计算结果则必然使半径变小,圆心位置发生偏移。
(2)对于轮廓仪等仪器采用直角坐标对圆轮廓进行测量评定时,采用的是采样点到圆边缘的距离;而根据最小二乘法的定义应该是实测值与相应圆上点的理论值之间的误差。因此,以此距离代替误差必然会带来分析结果的误差。
2 Newton迭代法对最小二乘圆误差的修正
现针对上述两种问题,分别提出不同的修正方法。
2.1 问题1的修正
根据圆的方程,点(xi,yi)到圆心的距离与半径的差为:
(9)
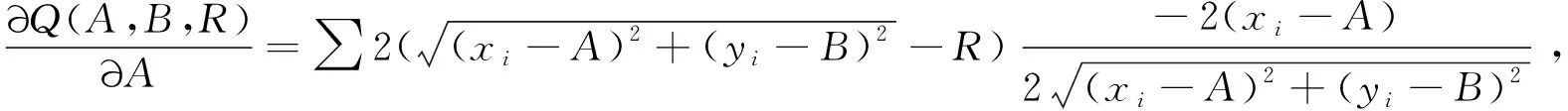
按照Newton迭代法[3],则有:
(10)
(11)
(12)
ΔA=Ak+1-Ak
(13)
ΔB=Bk+1-Bk
(14)
ΔR=Rk+1-Rk
(15)
取(6)~(8)式中的(A,B,R)为计算的初值(A0,B0,R0),根据测量需要的精度,计算(ΔA,ΔB,ΔR)即可。
2.2 问题2的修正
根据圆的方程R2=(xi-A)2+(yi-B)2有:
在直角坐标系中,误差为:
(16)
2.2.1 球体的修正
测量球体等凸面向上的圆形轮廓时:
(17)
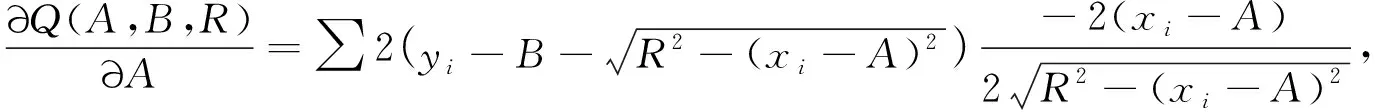
按照Newton迭代法,则有:
(18)
(19)
(20)
2.2.2 沟道的修正
测量沟道等凸面向下的圆形轮廓时:
按照Newton迭代法,则有:
(22)
(23)
(24)
同样,取(6)~(8)式中的(A,B,R)为计算的初值(A0,B0,R0),根据测量需要的精度,计算(ΔA,ΔB,ΔR)即可。
3 结束语
利用极坐标的仪器采用最小二乘圆法对圆轮廓进行测量评定时,如果不进行修正,因为圆心位置的偏离和半径的计算误差,会导致圆度误差的评定出现偏差,圆度值越大或工件偏心越大,误差就越大,特别是偏心带来的圆度误差在进行精密测量时有时可以达到5%~15%。采用玻璃半球对仪器的精度进行评定时,虽然圆度值很小(0.05 μm以内),但不同的偏心值仍可造成10%左右的误差;采用椭圆标准件对仪器进行放大倍数的校正时,不同的偏心值甚至会造成15%~20%的测量误差(多次测量的重复性),给仪器的校准及评定带来问题。通过Newton迭代法修正后,圆度值呈现一定的变化,最终趋于稳定,可以将重复性误差控制在0.1%~1%以内,相应提高了仪器的精度。
利用直角坐标的仪器采用最小二乘圆法对圆轮廓进行评定时,测量误差会呈现S形的变化。不仅圆心位置和评定半径发生变化,误差的本身也出现变化,从而整个圆轮廓的半径一致性也变差。通过Newton迭代法的修正可以消除部分S形误差(因为测杆的物理因素以及上下坡等因素也会带来部分S形误差),并可将同测量段的半径和圆心位置一致性稳定在0.5%~1%以内。

