三维裂纹扩展时动态应力强度因子的有限元研究

王光军 熊峰

（中国船舶重工集团公司712研究所，武汉 430064）

工程中很多构件受动载荷作用，例如：柴油机气缸内气体燃烧时受动态内压作用，气缸内腔经气体燃烧膨胀将出现龟裂，继续燃烧膨胀裂纹将不断扩展，可能产生疲劳破坏等等。实际上，三维裂纹扩展时动态应力强度因子的求解是一个较为困难的问题。由于增加了一个时间变量，不仅在数学处理上困难，在物理上也很复杂。对于三维问题应力强度因子，目前尚不能获得精确的解析解。而三维问题的数值分析，由于裂纹尖端奇异性的复杂性，以及计算工作量大等因素，使研究受到一定的限制。本文主要利用有限元软件ANSYS计算三维裂纹扩展时动态应力强度因子[1]，能为动态应力强度因子的计算、分析提供帮助和指导。

1 三维裂纹扩展时动态应力强度因子有限元分析

1.1 分析思路

对于线性弹性均匀介质，当载荷随时间变化，稳定裂纹顶端的渐近位移场与静态情况完全类似。对于平面I型问题

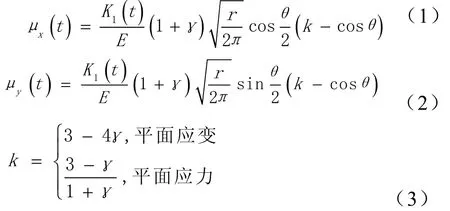
对于动态载荷下静止裂纹，裂纹尖端应力场和位移场公式与静态载荷下的类似。通过裂纹面上各点处垂直于裂纹面的位移，在平面应变情况下，由式(1)，式(2)，式(3)可得

(4)式中位移µy(t)为相应时刻裂纹面上各点处垂直于裂纹面的位移，可由上述的有限元法求得，外推到裂纹尖端求出r=0处的K1(t)值，即为所求动态应力强度因子。

1.2 三维裂纹扩展基本方程

动态随机载荷导致裂纹的随机扩展，如果将构件的动态干扰理解为围绕裂纹尖端周围材料的运动[2]，则其边界条件为：

同时满足两个剪切方程非零：

构件不受力的情况下，裂纹扩展方程可写为：

其中：c2=（µ/ρ）1/2是剪切速度，µ是剪切系数，ρ是物体的质量密度。

1.3 构件裂纹扩展数学模型

将所研究的构件进行有限元离散化处理，其运动扩展方程的矩阵形式[3]如下:

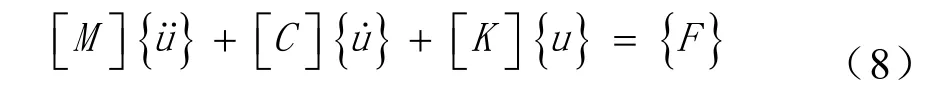
其中：[M]、[C]、[K]分别为结构的总质量矩阵、结构的阻尼矩阵、结构的总刚度矩阵；{u}为结构的节点位移列阵；{F}为节点等效载荷列阵；{}为节点位移二阶导数列阵，即加速度列阵；{}为节点位移的一阶导数列阵。

求解线弹性有限元动力方程可采用Newmark逐步积分法，得到稳定结果。在时刻t+Δt由运动方程得

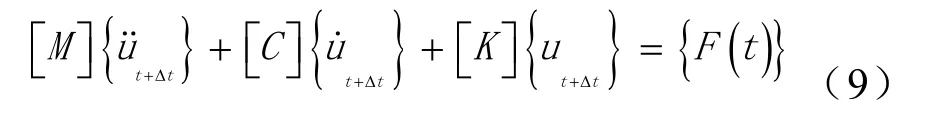
速度与位移由（10）式给出

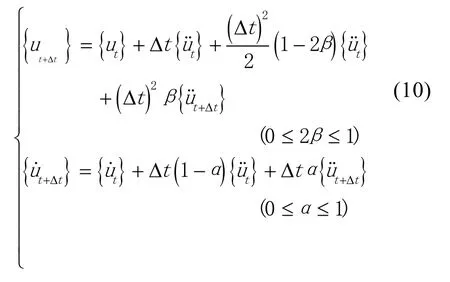
其中α、β为控制算法精度和稳定的两个参数。

如果t=0时的初始位移和初始速度为{u0}与{0}，则由式(8)求得初始加速度

再根据式(9)— (11)式，求出下一时刻△t的{uΔt}，{Δt}，{Δt}，由此即可得到所有时间离散点上的位移、速度与加速度，进而可以求得各个时刻的应力、应变和应力强度因子。

1.4 加载时间步长的确定

动态有限元程序，是通过逐步时间积分来解动力方程，需要选定合适的加载时间步长，加载时间步长△t选得过小，将增加计算时间，加载时间步长△t选得过大将影响计算精度，本文参考文献[4]中所建议的公式确定时间步长。

△t≤ Δl/C，△t为单元最小尺寸，c为最大纵波波速。参考t△ ≤ Δl/C可得对不同裂纹长度计算取△t=1.0×10-5～3.0×10-4s时能得到较好的结果。

1.5 单元形式的选取和裂纹扩展运动的求解

本文采用APDL参数化语言编制三维裂纹模型，同时结合 ANSYS子模型技术进行分析[5]。由于裂纹顶端区域应变场具有r-1/2阶的奇异性，为此在裂纹顶端采用四分之一中点奇异等参元。对于线性弹性问题，这种单元构造自动生成r-1/2阶的奇异性。其他部位采用标准八节点等参元。

求解裂纹扩展运动的主要采用模态叠加法。有限元法是计算动态K1(t)因子的有效方法，但求解动态问题需逐步加载计算，时间步长很小，很费机时。本文引用叠加原理，将每一种动态载荷曲线分解为很多微小的分级加载叠加组成，同时由于用APDL参数化语言编制的三维裂纹程序中可以灵活地修改相关参数，这样大大减少了有限元法的计算量。

本文按照模态叠加法步骤计算所有时间离散点上的位移、应力等信息，再利用软件求解静态应力强度因子，计算出某个时间点上的应力强度因子。从而可以得到应力强度因子和时间的动态关系。

2 算例分析

为了模型的普遍性，采用断裂力学中常见的有限尺寸圆柱体中深埋圆裂纹模型[6，7]为研究对象。圆裂纹示意如图1。

图1 圆裂纹示意图

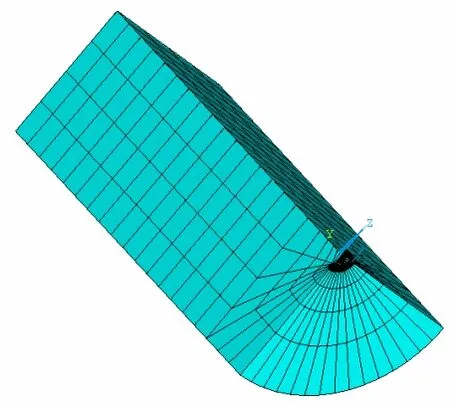
图2 八分之一圆柱体的中心裂纹模型

图3 裂纹局部放大图

考虑到对称结构，建立八分之一圆柱体的中心裂纹模型，如图2，裂纹局部放大如图3。取有限立方的八分之一建立模型的尺寸Ro；裂纹尺寸位于a处，圆柱高度为h，材料及模型参数具体尺寸如表1。选择单元MESH200和单元SOLID95,在单元属性中将 MESH200设置为KEYOPT(1)=7。用ANSYS编制的APDL程序计算裂纹深度a分别为: 5 mm、9 mm、15 mm、23 mm、27 mm，时间分别为2 ms、2.5 ms、3 ms、3.5 ms、4 ms、5 ms时的应力强度因子。在裂纹尖端用退化三角形奇异等参元，其余地方用标准等参元。

表1 材料及模型参数

本文采用突加载荷，如图4，其中σ0（t）=100 MPa。对不同裂纹长度的动态应力强度因子的有限元计算结果列入表2中。图5所示为裂纹尖端应力场，典型的应力集中现象。

图4 载荷示意图

表2 突加载荷动态强度因子的结果

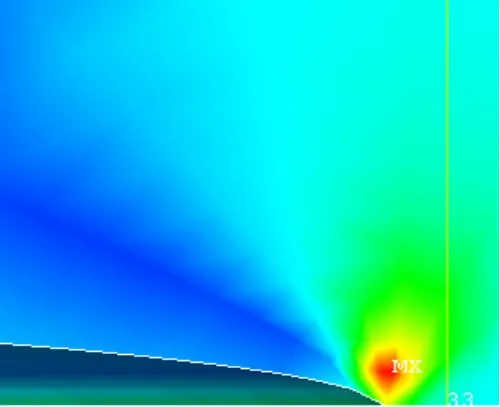
图5 裂纹尖端应力场

图6 载荷作用下裂纹尖端扩展图

图6为载荷作用下裂纹尖端位移扩展过程。最后利用各个时间点和相应的应力强度因子作图，得出动态应力强度因子随时间的变动图，如图7。

图7 动态应力强度因子图

本文模型的正确性和求解静态应力强度因子的准确性可以通过查看《应力强度因子手册》[8]对比得到。根据计算静态应力强度因子的步骤，这样可以计算出理论值为K1（t）的误差。本文算出的应力强度因子与《应力强度因子手册》中结果最大误差为 4.7%，证明模型及网格划分良好，计算结果精确。

3 结束语

(1) 利用 ANSYS建立三维模型的方法是多种多样的，本文主要考虑的圆柱体中心圆裂纹的结构。还可以利用相同的单元和建模方法建立其他典型裂纹结构，如中心穿透裂纹，椭圆裂纹等。

(2) 通过与算例的比较，可以认为利用ANSYS的 APDL参数化语言编程建立三维裂纹模型是可行的，有限元法是计算动态K1(t)因子的有效方法，本文提供的合理计算方案，也可为其它结构件动态K1(t)因子的计算作参考。

[1] 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社，2001.

[2] 范天佑. 断裂动力学原理与应用[M]. 北京:北京理工大学出版社，2006

[3] 王助成，邵敏. 有限单元法基本原理和数值方法[M].第二版. 北京: 清华大学出版社, 1997.

[4] V MURTI S VALLIAPPAN. Engineering Fracture Mechanics. 1986, 23(3): 585-614.

[5] ANSYS，Inc. ANSYS Coupled-Field Analysis Guide Release7.0.

[6] Chen Aijun. Study on Dynamic Stress Intensity Factors of Disk with a Radial Edge Crack Subjected to External Impulsive Pressure. Acta Mechanica Solida Sinica,Volume 20, Issue 1, March 2007, Pages 41-49.

[7] Yong-Dong Li, Kang Yong Lee. Dynamic Stress Intensity Factors of Two Collinear Mode-III Cracks Perpendicular to and on the Two Sides of a Bi-FGM Weak-discontinuous Interface. European Journal of Mechanics - A/Solids, Volume 27, Issue 5,September-October 2008, Pages 808-823

[8] 中国航空研究院. 应力强度因子手册. 北京:科学出版社，1993.