一种新型的非线性系统模型参数辨识方法

耿永刚

(常州机电职业技术学院，江苏 常州 213164)

非线性模型参数估计是控制领域研究的重要问题。目前已有许多成熟的系统辨识和参数估计方法，如最小二乘法[1]、极大似然估计法[2]、神经网络用于参数辨识法[3]、遗传算法[4-5]等。但是最小二乘法和极大似然估计法都是基于过程梯度信息的辨识方法，其前提是可微的代价函数、性能指标和平滑的搜索空间。但在实际应用中，由于获得的数据含有噪声或所辨识的系统非连续，使得这一条件难以满足；利用神经网络进行系统参数辨识虽然具有以任意精度逼近非线性函数的能力，但是在实际应用中，只有选择了合适的网络结构，才能获得好的结果，但选择合适的网络结构往往是非常困难的；利用遗传算法特有的复制、交叉和变异功能以及群体寻优的方式来克服陷入局部最优解，可获得较好的模型参数估计，但是遗传算法需涉及到繁琐的编码、解码过程以及较大的计算量，而且整个种群是比较均匀地向最优解区域移动，因此其搜索效率不高。

由Kennedy等人提出的微粒群(PSO)算法[6-13]是一种有效的随机全局优化技术，已经被证明是一种很好的优化方法。PSO算法对优化目标函数形式没有特殊要求，而且没有遗传算法中的交叉、变异算子，各个算子根据自己的速度来搜索，整个搜索过程跟随当前最优解进行。目前已在许多函数优化、网络训练、参数整定等领域中得到了广泛应用。本文借助PSO算法的群体寻优能力，通过对算法的改进，将其应用到对非线性系统模型参数辨识中。

1 问题描述

对于描述过程的模型一般形式为：

其中，x为系统输入，y为系统输出，θ为待估计模型参数，e是均值为 0、方差为 δ的噪声。

参数辨识就是在模型结构已确定的情况下，根据已知的观测数据对(xi，yi)，i=1，2，…，n 求解偏差平 方和 J(θ)为最小的 θ值。

可以看到其实质就是将模型参数辨识问题转化为函数优化问题。

2 微粒群优化(PSO)算法及其改进

2.1 基本PSO算法原理

PSO算法是一种新型演化计算方法。其中，“群”来源于Millonas在开发应用于人工生命(artificial life)的模型时所提出的群体智能的5个基本原则[14]。而“微粒”则是一个折衷的选择，一方面将群体中的成员描述为没有质量和体积的个体；另一方面赋予其速度和加速度。

设第 i个微粒的位置为 Xi=(xi1，xi2，…，xiD)，其速度为Vi=(vi1，vi2，…，viD)。 该微粒其所经历的历史最好位置记为 Pi=(pi1，pi2，…，piD)，也称为 Pbest，记全体所有微粒经过的最好位置为 Pg=(gi1，gi2，…，giD)，也称为 Pgest。按追随当前最优微粒的原理，对第t代的第i个微粒，PSO算法根据方程(3)计算第t+1代的第j维的速度和位置。

此外，微粒的速度vi被一个最大速度所限制。如果当前对微粒的加速导致它在某维的速度vij超过该维的最大速度 vmax，j，则该维的速度被限制为最大速度 vmax，j，使得粒子不至于因为飞行速度过高而跳过可能的优化解。

2.2 PSO算法的改进

通过对式(3)、式(4)分析发现，如果粒子群的历史最优粒子位置Pgest在较长时间内没有发生变化，在粒子群体快接近Pgest时，其速度更新将由历史速度决定，于是速度将越来越小，粒子群呈现出强烈的“趋同性”，表现在式(3)中的第2项和第3项接近于0。这种“趋同性”加快了算法的搜索速度，但是却减弱了群体开拓新的搜索空间的能力。如果该最优位置为一局部最优点，则算法很容易陷入局部最优，发生早熟现象。通过粒子群优化算法的搜索机理分析发现，无论是早熟收敛还是全局收敛，微粒群中的粒子都会出现“聚集”现象。针对这个问题，本文对PSO算法作了以下改进：在微粒群从第t代向第t+1代“飞翔”时，粒子除追随个体极值Pbest和全局极值Pgest外，还追随从微粒群中随机选取的某个粒子个体极值 Pn，则式(3)改写为：

式中，c3为非负常数，一般取 0.5；为[0，1]的随机数，根据仿真实验，的取值范围在 0～0.5之间时能获得较好的效果；qij是随机选取粒子的位置。在粒子的飞翔迭代公式中增加Pn后，由 Pbest、Pgest和 Pn三者共同向下一代提供信息，粒子获得的信息量增大，从而可能更快地找到最优解。同时Pn的权重系数很小，相当于扰动信息，增加了粒子的多样性，避免算法过早收敛。式(4)和式(5)组成后称之为改进的PSO算法MPSO(Modified PSO)。

2.3 算法设计

采用改进PSO算法进行非线性系统模型参数辨识研究，设计出的实现算法为：

(1)根据优化命题的复杂性，确定群体规模m和搜索空间维数D，并初始化群体的速度和位置；

(2)根据式(5)，计算每一个微粒新的速度和位置；

(3)根据优化目标确定算法的适应度函数，适应度函数可以根据具体的情况来确定；

2.1 开发主体环保意识薄弱 旅游资源作为一种资源，不论是可再生还是不可再生，在其使用过程中不可避免会受到破坏，绝大多数生态旅游资源都具有破坏容易恢复难的特性。随着景区知名度的提升，加上游客日益多样化的需求，旅游目的地不得不想办法对资源进行深度的挖掘和再次开发。受经济利益的驱使，常常使得旅游开发具有盲目性，可能会使得资源过度开发而超过自身恢复限度。张家界国家森林公园，由于对修建性建设项目控制不够，造成水质污染，曾被联合国教科文组织亮出黄牌警告，当地政府为了恢复景区原貌，花费了上亿元人民币。

(4)对每个微粒，将其适应值与其经历过的最好位置Pi作比较。如果较好，则将其作为当前的最好位置Pi，否则继续执行下一步；

(5)对每个微粒，将其适应值与全局所经历的最好位置Pg作比较。如果较好，则将其作为当前全局的最好位置Pg，否则继续执行下一步；

(6)判断算法是否满足终止条件。若达到终止条件，则算法停止，返回当前最优个体为结果，否则，返回第二步继续。

3仿真研究

为了验证利用改进PSO算法进行非线性模型参数估计的有效性，本文以谷氨酸菌体生长模型[5]参数优化估计为例进行了仿真研究。

菌体种子接入发酵罐以后，就在罐内按自然规律生长繁殖，在整个发酵期间，若无杂菌和噬菌体的侵袭，罐内外没有大规模菌体迁移。菌体在发酵罐内的自然生长繁殖过程可以用Verhulst方程来描述[5]:

在工业生产的实际过程中，鉴于接入发酵罐中的菌体有一个适应环境的过程，而菌体的增殖有一段时间的滞后 τ1，为此， 将上式改写为:

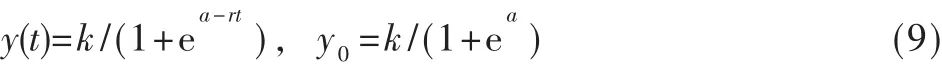
式(8)即可作为菌体在发酵罐内的生长模型。其中y(t)为菌体浓度，t为菌体生长时间，r、a、k为待定模型参数。

利用改进的PSO算法进行模型参数估计的目的是要确定菌体生长模型中的模型参数r、a、k使得实际观测值与模型估计值有较高的拟合度。本文利用参考文献[5]中提供的实际观测数据，通过改进的PSO算法对模型参数进行估计，见表1。

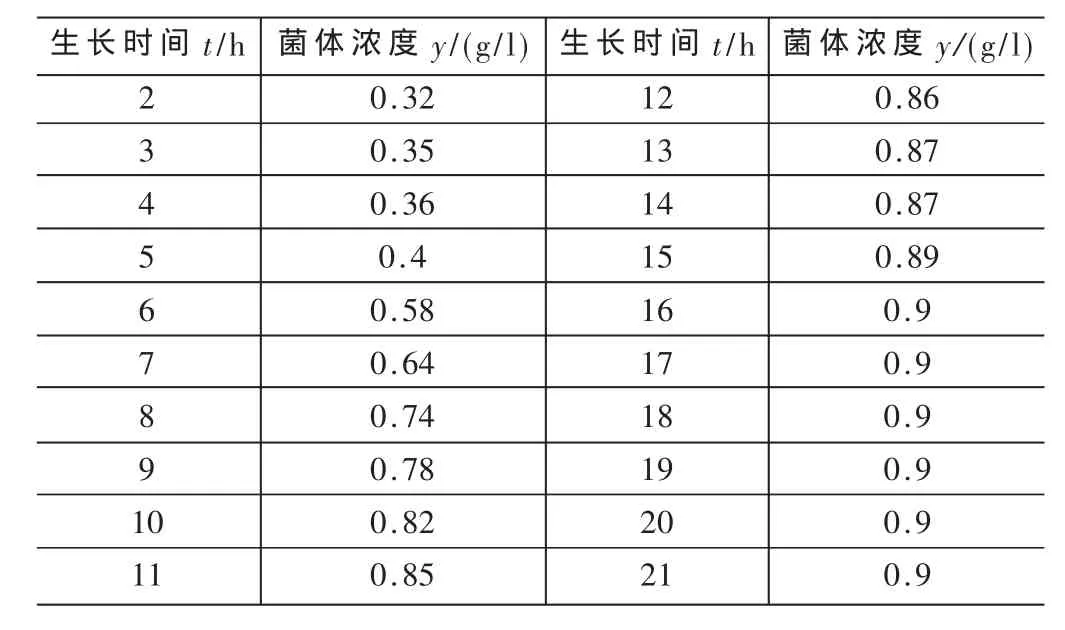
表1 菌体浓度实际观测数据

改进的PSO算法适应值函数采用如下偏差平方和形式：

其中yi为菌体浓度的实际观测值，为菌体浓度的模型估计值，n为用于模型参数估计样本个数。

改进PSO算法参数为：种群规模m=20；惯性权重w从1.2逐渐线性衰减到0.1；加速度常数为C1=C2=C3=0.5；因本文针对系统模型的三个参数进行估计，故取D=3；待估计参数 r、a、k 的定义域区间为[0，5]。

根据表1中的观测数据，利用PSO算法进行参数估计，并与人工神经网络(ANN)、标准遗传算法(SGA)、改进遗传算法(IGA)、标准PSO算法4种方法进行了比较。表2给出了模型参数估计结果。

表2 菌体生长模型参数估计结果

为了验证本文方法的有效性，将表2中的5种算法得到的估计值分别作为模型参数，并以表1中的实际观测数据作为检验样本，进行模型拟合度的比较。表3是谷氨酸菌体浓度实际观测值与模型拟合值，采用剩余标准差式(11)作为评价指标，表4是5种算法分别对应的剩余标准差值。

从模型拟合值和模型剩余标准差的比较结果可以看出，基于MPSO算法的模型参数估计精度略高于ANN、SGA、IGA、PSO 算法， 而采用 ANN、SGA、IGA 3种算法也可得到较好的拟合效果。但从5种算法的实施过程来看，MPSO算法简单，需要调整的参数较少，易于编程实现、计算量小，适于在线辨识。可见将MPSO算法用于非线性模型参数估计是有效、可行的。

表3 菌体浓度实际值与模型拟合值的比较

表4 5种算法对应的模型剩余标准差

本文研究了用改进的PSO算法解决非线性模型参数估辨识问题，并以实例进行了验证。实验结果证明了基于改进的PSO算法的非线性模型参数估计是有效、可行的。从而为非线性模型参数估计问题提供了一种新途径。

[1]仇振安，何汉辉.基于广义最小二乘法的系统模型辨识及应用[J].计算机仿真，2007，24(10):89-91.

[2]马世桡，卢建伟.极大似然估计法在高压断路器可靠性分析中的应用[J].沈阳工业大学学报，2007，29(1):41-43.

[3]董泽，黄宇，韩璞.量子遗传算法优化RBF神经网络及其在热工辩识中的应用[J].中国电机工程学报，2008，28(17):99-104.

[4]夏秀渝，周激流.一种混合遗传算法及其在线性系统辩识中的应用[J].四川大学学报，2005，37(1):104-107.

[5]蔡煜东，陈常庆.用遗传算法辨识发酵动力学模型参数[J].化工学报，1995，46(3):338-342.

[6]ZHONG Wei min， LI Shao Jun， QIAN Feng. θ-PSO:a new strategy of particle swarm optimizition[J].Journal of Zhejiang University SCIENCE A， 2008，9(16):786-790.

[7]李炜，石连生，梁成龙.基于 PSO-LSSVM的研究法辛烷值预测建模[J].化工自动化及仪表，2008，35(2):25-27.

[8]CUI Guang-Zhao， QIN Li-Min， LIU Sha.Modified PSO algorithm forsolving planargraph coloring problem[J].Progress in Natural Science， 2008，18(3):353-357.

[9]成伟明，唐振民，赵春霞，等.基于神经网络和 PSO的机器人路经研究[J].系统防真学报，2008，20(3):608-611.

[10]刘晓峰，陈通.PSO算法的收敛性及参数选择研究[J].计算机工程与应用，2007:43(9):14-17.

[11]YUHUI S，EBERHART R.Proceedings of the 7th annual conference on evolutionary programming[C].Washington:IEEE Press，1998.

[12]YUHUI S，EBERHART R.Proceedings of the congress on evolutionary computation[C]， Washington:IEEE Press， 1998.

[13]XIE Xiao Feng， ZHANG Wen Jun， YANG Zhi Lian.Overview of particle swarm optimization[J].Control and Decision， Shenyang， 2003，18(2):129-134.

[14]MILLONAS M M.Swarms phase transition and collective intelligence[M].MA:Addison Wesley，2004.