Turbo码中伪随机交织器盲识别方法

张伟杰，张 玉

(解放军电子工程学院，安徽 合肥 230037)

利用Turbo码的数字通信具有低截获和抗干扰的特性，在现代军事通信和CDMA系统中得到了广泛应用。在非协作方式下，这些特性使直扩信号的检测和盲估计变得更加困难，成为现代通信侦察中的一个研究难点。在信号截获领域，在没有任何先验知识的情况下，为了实现对Turbo码的盲识别，必须对伪随机交织器进行盲识别，这也是其中的难点。因此，对伪随机交织器中的伪随机序列的估计是信息截获成功与否的关键。

通过对伪随机交织器原理分析，发现其原理同扩频通信中的PN码发生器原理类似，因此将直接序列扩频信号PN序列盲估计方法移植到Turbo码中伪随机交织器的盲识别中去。仿真结果表明，该方法可以在发送端没有任何先验知识的情况下，适用于对m序列、Gold序列等伪随机交织器的盲识别。

1 伪随机交织器原理

设输入的信息序列为UN，以一维数组的形式存储。为了乱序数据，需要建立一个额外的数组，并称为索引数组，存放着N+1个随机数据，分别对应着不同的随机地址，随机地址可通过程序中随机数的调用来获得，并且之间的每一个数据都必须出现且仅出现一次。图1为N=11时的伪随机交织器的示意图[1]。

图1 伪随机交织示意图

实际中的交织器通常采用m序列来产生随机数，图1表示的只是m序列一个周期的示意图。由m序列的性质可知，在一个周期内的m序列各个状态中除了全零状态以外，其他状态只在m序列中出现一次。以m序列作为读写地址时，m序列状态的唯一性保证了地址的唯一性，同时也保证了输出数据的唯一性和随机性。

通过对伪随机交织原理的分析，想要得到原始信息序列，就需要对数据索引组进行恢复，即对伪随机交织器产生的伪随机序列进行盲恢复。

2 m序列周期估计

估计伪随机交织器中伪随机码周期是伪随机序列估计的必要条件，估计伪随机码周期可以借助于对PN码的周期估计，主要有二次谱法[2]、周期谱法[3]和基于二阶循环统计量法[4]。下面借助基于二阶循环统计量的方法估计m序列周期。设截获到的交织信号形式为：

式中，u(n)为信息码，p(n)为伪随机交织器产生的 m序列。

式(2)、式(3)中，uk，pk∈{0，1}，q(·)为幅度 为 1 的矩 形 脉冲，Fs为采样频率，To为m序列周期。

其算法实现的步骤如下：

(1)由于m序列具有周期性，其在时域仍具有循环平稳性，且以m序列的周期为周期。若信号s(n)的自相关是周期的，即存在 T≠0，使 Rs(n，m)=Rs(n+To，m)成立，则信号s(n)是循环平稳的。对Rs(n，m)进行傅里叶级数展开，可得：

这样就可以得到循环自相关函数的一致估计为：

式中a为循环频率，N为数据长度。所以对输入信号，可利用式(5)估计其循环自相关函数。

(2)可以证明，交织信号的循环自相关函数由多个冲激函数组成，这些冲击函数位于信号的各个谐波频率处k/To(k=0，±1，±2，…)，相邻谱线的间隔即是 m 序列周期。因此，通过估计相邻循环频率间的差值可以得到m序列周期的估计。根据对称性，在正频率部分设置门限h，计算大于h的相邻循环频率值间的最小差值dmin。设置门限是为减少噪声影响，提高估计精度。

(3)估计 m序列周期 To=1/dmin。

3 m序列起始点与码序列估计[5]

为了正确估计伪随机交织器产生的m序列，以至进一步解扩数据信息，还需要估计信息码与m序列的同步起始点。本文采用分段互相关法来估计信息码的起始点Tp。

在已知m序列周期To的条件下，设采样起始点与数据调制起始点相距为Tp，将接收到的信号按照To分段，当分段的起点与数据调制起点重合时，则每一个分段对应的向量都应包含一个完整的m序列，此时得到的各个向量组之间有最大的相关性。为此，采用计算段之间互相关最大值的方法实现调制起始点的估计。算法的步骤如下：

在晨会、少先队活动中宣传“自己的事自己做”，并举行各类小竞赛激趣，强化意识。课外，主动与部分学生家长联系，召开家长会，举行“家长开放日”活动保证了学校、家庭、社会影响的一致性。运用情感激励，榜样激励、奖励激励等手段，把自主管理渗透到各科教学、班级活动的每一个环节，多层次、全方位激发学生参与管理的动机，使学生置身于自主管理的客观环境中，产生一种参与管理的需要。

(1)以m序列周期To分段截获解调带直扩信号。设数据总周期T=Tp+(N-1)To，其中Fs=1，则数据段数为m=N-1，起始位置为第1个信息码调制对应的m序列内的第k个采样点，用矩阵表示为：

式中，每一行元素表示1个分段内的To个向量，共有m行。

(2)计算分段数据向量两两间的相关函数，得到相关矩阵为：

式中，rij为第i个分段和第j个分段的相关；Rk为 1个对称矩阵。

(3)求矩阵Rk中所有元素的绝对值之和nk。

(4)k从 1～To取值，求 nk，最大的 nk所对应的 k值即为信息码与PN码波形同步起始点。

通过上述的方法就可以得到伪随机交织器产生的m序列，这个难点解决之后，为Turbo码的盲识别扫清了前期的障碍。因为Gold序列与m序列有相似的性质，通过下面的仿真发现，此方法同样可以对产生Gold序列的伪随机交织器进行盲识别。

4 仿真分析

[4]中，已经对m序列周期、起始点和码序列估计方法的性能进行了仿真分析，得到了在低信噪比下也可得到较高正确率结果，对此不再证明并给出仿真图。本文则对Turbo码下的基于m序列以及Gold序列的伪随机交织器部分进行仿真，验证方法引用的正确性。

首先对基于分段多重互相关平均法的m序列估计方法进行仿真。信息码位数N=300，码周期To分别取42和71，采用二重相关估计m序列。进行100次Monte-Carlo仿真实验，得到的m序列正确估计概率曲线如图2所示。由图可知，当信噪比SNR＞-8 dB时，算法对m序列的正确估计达到100%；在SNR=-9 dB时，仍可以达到75%的正确估计概率。

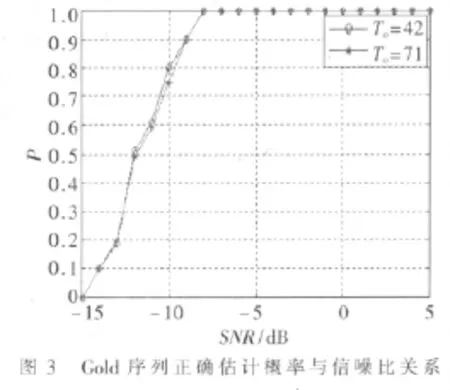
利用同样的环境与方法再对交织器产生的Gold序列进行仿真。得到如图3的仿真图。同样可以看到在低信噪比的环境下，引用的算法对Gold序列也有较好的正确估计率。

随着Turbo码的广泛应用，对Turbo码的盲识别必将成为信息截获领域中的热点问题。其中不可避免的难题就是，如何识别其中的随机交织过程，即对伪随机交织器实现盲识别。本文借助于扩频通信中对PN码进行盲识别的二阶循环统计量和分段互相关法，来解决伪随机交织器的盲识别问题。仿真结果表明，根据m序列的特性，利用上述方法完全可以对伪随机交织器产生的伪随机序列进行准确估计，从而为Turbo码的盲识别做好必要的准备，因此具有广泛的应用前景。

参考文献

[1]白宝明，马啸.随机交织器的设计与实现[J].通信学报，2000，21(6):6-11.

[2]ZHANG Tian Qi，ZHOU Zheng Zhong.Algorithms for period and sequence estimation of the PN code in DS-SS signals[J].Systems Engineering and Electronics， 2005，27(8):1365-1368.

[3]DOUGLAS A，BODIE H J B.Carrier detection of PSK signals[J].IEEE Transactions on Communications， 2001，49(3):487-496.

[4]罗军辉，姬红兵，江莉.直接序列扩频信号 PN序列盲估计方法[J].电子科技大学学报，2008，37(4):408-492.

[5]JIN Yan， JI Hong Bing， LUO Jun Hui.A cyclic-cumulant based method for DS-SS signal detection and parameter estimation[J].Acta Electronica Sinica， 2006，34(4):634-637.

[6]吕明，张红波，唐斌.基于 E-PASTd的盲扩频码序列估计算法[J].电子科技大学学报，2007，36(5):886-888.