基于欠采样和ZFFT的流速动态跟踪测量方法

李建立 ，刘纪元 ，2，焦学峰

(1.沈阳航空工业学院，辽宁 沈阳 110136；2.中国科学院声学研究所，北京 100100；3.北京航瑞博泰科技有限公司，北京 100102)

明渠流量测量中需要测量水速和水深两个关键参数。新型的流量计大多采用超声波进行测量，依据多普勒原理求解渠中水的速度，并依据发射和接收脉冲信号的时间差估计渠中水的深度。利用带通欠采样技术，选择合适的采样频率，可以完全恢复原信号，同时，可大大降低采样速率。另外，采用带通欠采样技术测速和测深可以分时利用前端抗混叠带通滤波器，达到有效地利用硬件资源，简化了设计，节约了成本。

但是共用前端带通抗混叠滤波器，可致使采样率较高。其原因是：在明渠测深中需要一个宽带脉冲信号。相对而言，明渠中流速的测量其有效带宽较窄。所以，抗混叠带通滤波器的设计，须按照带宽较宽的参数设计。除此之外，中心频率越高，带通的窄带性越难做到，这也是导致采样率较高的原因之一。为了提高测速分辨率，设计中引入局部频带细化技术ZFFT(ZoomFFT)，大大提高了速度分辨率。实现方法为：通过跟踪水的瞬时动态流速范围，确定一个较窄的局部动态频带，通过软件中设计的抽取带通滤波器对关注的局部频带进行选择和抽取，然后进行频带的细化和分析。文中给出了带通欠采样技术下ZFFT实现的具体过程。事实证明，这种方法具有计算量小的特点，易于实现，而且可以达到很高的测量精度。

1 多普勒测速原理

多普勒现象：向以相对运动的目标发射信号，回波信号的频率和原来发射信号频率不同，产生频率差，这一现象称作多普勒现象[1-3]。

利用这一原理在水中发射水声信号，水中运动的杂质颗粒反射波的频率，反映了水体的流速。关系如下：

式中，φ为换能器安装角(波束方向与水平面的夹角)；c为超声在水中的传播速度，常温下大约1 500 m/s。

实验中发射信号频率采用1 MHz，水声换能器与水速的安装夹角为45°，若认为水速 5 m/s时，为实际水渠的极限值，由式(1)可以反推多普勒频偏为4.7 kHz。取5 kHz为最大频偏，且考虑流速的方向性，测速有效带宽范围为：0.995 MHz～1.005 MHz。为了提取多普勒信号，本文采用带通欠采样的技术。通过欠采样把发射信号的频率移到低频的某一对应频率处，如图1所示A点，回波信号频谱可以存在OA或AB两个区内，回波信号与发射信号(对应位置A点)坐标差反映了多普勒频偏。把发射信号移到中频位置A点，是为了能对流水的方向做判定。

图1 多普勒频率搬移示意图

2 带通欠采样及其采样率的确定

设信号的频带范围为(f1，f2)，f1＜f2，若 采样频率 fs满足式(2)：

其中，2＜n＜[f2/B]，符号[]表示取整。 满足式(2)可保证信号频谱不发生混叠及完全可恢复原信号，这就是带通采样定理[4]。实际应用中，信号进入数字系统前，f1代表带通滤波器的下端截止频率；f2代表上端截止频率。B=f2-f1表示带宽。带通欠采样可以采用比传统技术低得多的采样率，表示数据采集性能的提高及功耗和成本的降低[5-6]。

为了降低设计成本，测速测深采用分时利用同一抗混叠带通滤波器。设计中采用带宽B=60 kHz，中心频率f0=1 MHz，即带通范围为 0.97 MHz～1.03 MHz，这样既可以满足测速的带宽需求，又可以满足测深的带宽要求。但在测速中，其采样速率提高了很多。式(2)中，f1=0.97 MHz，f2=1.03 MH，n=10，则 201 kHz＜fs＜221 kHz，选择 留有一定的边界冗余采样率fs=204 kHz，则经欠采样后，搬移到奈奎斯特第一主频(15 kHz，25 kHz)，若在频谱分析中 FFT计算点数为N=2 048，则频率分辨率 △f=fs/N=99.6 Hz。代入式(1)，速度分辨率=10 cm/s。为了进一步提高速度分辨率，还需要在软件中对数据作细化处理。

3 动态跟踪流速范围，抽取局部频带细化处理

明渠流量中水速多普勒频带范围分布(0.995 MHz，1.005 MHz)频带内，其宽度为 10 kHz，然而在某一个时段渠中，水的流速变化对应的多普勒频带只占据频带上一个很窄的范围(速度变化是一个连续的过程，不可能发生速度值的跳变)。因此可以通过跟踪水的瞬时动态流速范围，确定一个较窄的局部频带。通过在软件中设计一个较窄的抽取带通滤波器选取出这个时段的局部频带，使得信号带宽变窄，采样速率下降，进而可以提高速度分辨率。

ZFFT技术关键是局部信号提取，并通过频谱搬移至低频，然后利用奈奎斯特采样定理，就能以很低的采样率进行采样(对局部频带的细化处理ZFFT技术可以查阅参考文献[7-8])。但是在欠采样下，依据欠采样的性质，可以很好地与ZFFT方法结合在一起。欠采样本身具有把频谱向低频搬移的特性。因此欠采样下可以简化这个步骤，带通欠采样下具体实现频带细化的过程如下：

(1)首先选择某一采样频率(满足式(2)，且采样率 fs×N≠1 MHz)，目的是在初次测量中，将1 MHz频率移到中频，且能判定流速方向。根据本次测量值的大小选择抽取带通滤波器。

(2)参照阈值。在流速变化过程中，当流速测量值超出某个阈值v1，采用临近较高频段的带通进行频带选取。当流速低于某个阈值v2时，采用临近较低频段带通。比如两个流速范围划分A(0，1.3 m/s)和 B(1.0 m/s、2.6 m/s)，分别对应抽取带通滤波器 A1和 B1，当流速 v大于v1=1.2 m/s时，采用抽取带通滤波器B1；当流速小于v2=1.1 m/s时，采用抽取带通滤波器A1，对频带进行抽取(设置阈值时，v1≠v2)。

(3)流速范围划分后，选择相应的带通，抽取相应的局部频带。依据局部频带带宽，确定重抽样倍数D。对采集到的数据进行重抽样(如仍做欠采样，频谱会被搬移到低频处，所以欠采样下ZFFT省去了移频过程)。

(4)进行快速傅里叶变换(FFT)分析。在上述步骤(2)流速范围划分下，对应带宽约1.25 kHz，可以选择D=64进行细化，这样得到的频谱的分辨率=204 kHz/64/2048=1.55 Hz，流速分辨率=1.6 mm/s。(无需频谱还原，测速只要求解出多普勒频偏即可)。

4 两次欠采样下流速方向的判定

对信号进行欠采样，在频域上是对频谱进行频谱搬移。0～fs称作奈奎斯特第一主频，在频域0～fs/2内的频谱有两种可能：(1)正向频谱的搬移；(2)负向频谱的搬移，两种搬移流速方向判定相反。

欠采样的频率选择：式(2)中，若取 n为偶数，则频带[0，fs/2]为负向频带频谱搬移；若 n取奇数，[0～fs/2]为正向频谱搬移，如图2所示。

设计中两次用到欠采样，最终的流速方向由两次欠采样共同决定。具体关系如表1所示。

在0～fs/2为正向频谱搬移，若回波信号频率变大则流速方向为正向向换能器流动；变小则方向相反。

在0～fs/2为负向频谱搬移，若回波信号频率变大则流速方向为逆向向换能器流动；变小则方向相反。

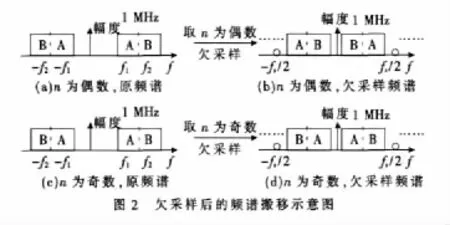
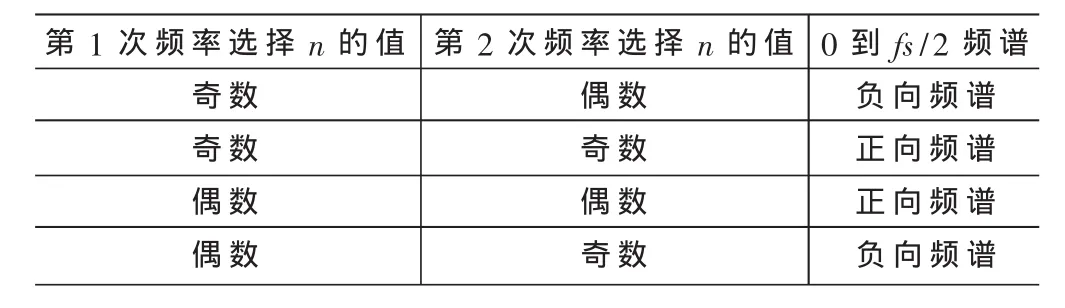
表1 两次欠采样后的频谱搬移特性

根据两次欠采样中n的奇偶性，判断(0，fs/2)频段内频谱是正向频谱搬移或是负向频谱搬移，进而可判断流速的方向。

5 在DSP平台上的流速测试实验

(1)水的流速范围分成 A(0，1.3 m/s)、B(1.0 m/s，2.6 m/s)、C(2.3 m/s，3.9 m/s)，并设 计相 应频带的抽取带 通滤波器及相应的阈值。

(2)发射信号为 1 MHz正弦波；水温 25℃；含沙量约5%；换能器与水平夹角45°(迎水安装)。测试水速在1.0 m/s以下，对应流速范围为0，1.3 m/s，相应抽取带通滤波器设 计 参 数 为 20 kHz/204 kHz×2，18.75 kHz/204 kHz×2。带入 式(2)，取 n=13 则 2.85 kHz＜fs＜3.26 kHz，取 fs=204 kHz/64=3.18 kHz作为重采样后的最终频率，此时分辨率为：204 kHz/64/2048=1.5 Hz，对应测速分辨率为1.6 mm/s(其他流速范围的抽取带通滤波器设计方法相同)。

(3)理论发射1 MHz信号经采样率fs=3.18 kHz(两次欠采样后的采样率)采样后，得到1.91 kHz余频。经计算占2 048个谱线的第1 228.6根线谱，由于栅栏效应的存在，可计算在第1 229根谱线有最大幅度谱。又因为第1 229根谱线在负频率轴，故在(0，fs/2)内占据 1 024-(1 229-1 024)=819根谱线位置。

(4)由第 1次欠采样 n=10，第 2次欠采样 n=13，由表1得知为负向频谱搬移。所以，如果多普勒回波信号频率大于1 MHz，谱线应该出现在其左侧，即谱线出现在小于819位置上。

(5)流速范围在(0，1.3 m/s)的计算方法：

(819-X)×1.6 mm/s。X表示谱线的加权均值。

实验1水静止条件下测得数据

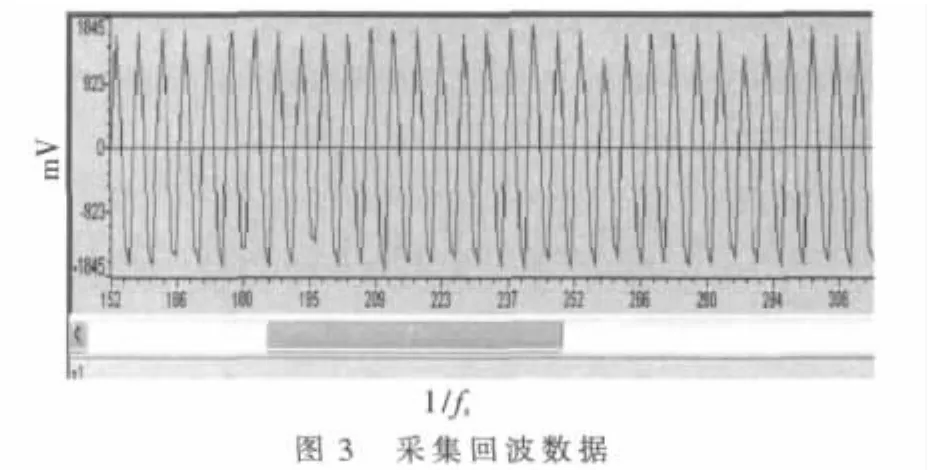
水静止条件下，测得回波信号及其频率，如图3、图4所示。

数据分析：水静止条件下，反射回波信号不存在多普勒现象。如图4所示，频谱分析后谱线在第819根谱线位置出现，测试数据结果和上述理论分析一致。

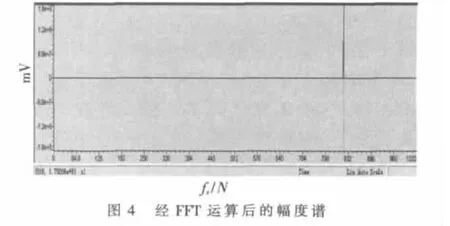
第819根谱线位置作为基频参考位置，多普勒信号FFT分析后谱线位置于此的差值d(819-719)，乘以频率分辨率，即可估计出多普勒频偏。例如：回波信号在719有峰值，则对应的频偏为：(819-719)×1.5=150 Hz

对应水的流速：(819-719)×1.6 mm/s=16 cm/s

实验2一定流速下测量数据

水速约 62.5 cm/s，测得数据如图 5、图 6所示。

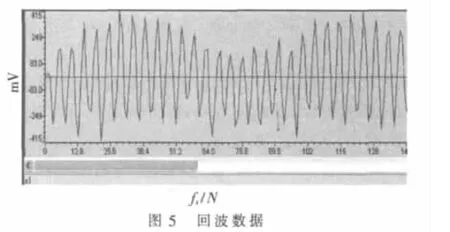
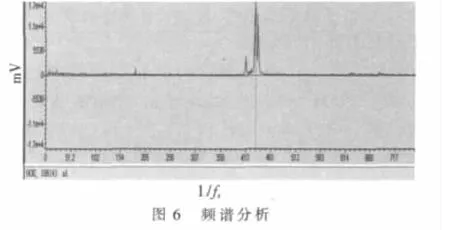
经过加权平均后可得本次的流速为61.76 cm/s。

多次测量求均值，测试结果如表2所示。

表2 三次实验数据(cm/s)

误差：0.54 cm/s。水速方向：向换能器流动。

从实验1可知，理论值和文中提到的动态跟踪测量方法、精度达到一致。流速分辨率完全可以满足工程要求，且计算复杂度小。实验2的数据表明，实验值和真实值之间的波动在允许的范围2 cm/s内。满足工程需求。

设计中利用欠采样的性质，对多普勒信号进行提取和估计，在多普勒信号的提取中充当着混频器的作用；在基于局部频带细化过程中起到了频谱搬移的作用。为了判定流速方向，把发射信号频率调到中频，可以根据欠采样性质判定流速方向。测量过程中一旦流速方向和流速范围确定，可以根据事先设置的流速阈值选择相应频段的抽取带通滤波器，对相应局部的频带进行选择抽取，进而做细化处理分析(欠采样下的ZFFT)。事实证明，这种方法大大提高了流速分辨率，而且可测流速范围也较宽。

[1]张羽，汪源源，王威琪.超声多普勒信号平均频率估计方法的比较研究[J].声学技术，2000，19(3)：127-129.

[2]孙兴亮.多普勒测速技术—信号处理技术[D].西安：西安电子科技大学，2005.

[3]陈方明，王浩.Doppler测速系统初速度的一种快速算法[J].国外电子测量技术，2005，24(7):41-43.

[4]张睿.带通欠采样技术在软件接收机中的应用[J].西安电子科技大学学报(自然科学版)，2000，27(3):327-328.

[5]周良将，梁兴东，丁赤飚.高精度相位特性测系统设计与实现[J].电子测量与仪器学报.2009:193-194.

[6]李慧光.欠采样频率的选取[J].传感技术学报，1998，12(4)：16-19.

[7]丁康，谢明，张彼德，等.基于复解析带通滤波器的复调制细化谱分析原理和方法 [J].振动工程学报，2001，14(1):30-35.

[8]罗守男.基于超声多普勒方法的管道流量测量研究[D].北京：清华大学，2004.