利用不等式的性质解物理题

王金聚

(浙江省温州中学,浙江温州 325000)

1 利用不等式的传递性

数学模型:如果 a＞b,b＞c,那么 a＞c.

例1.有4盏灯,接入如图1所示的电路中,L1和 L2都标有“220 V,100 W”字样,L3和 L4标有“220 V,40 W”字样,把电路接通后,最暗的灯将是

图1

(A)L1. (B)L2. (C)L3. (D)L4.

解析:由它们的额定电压、额定功率可以计算出4盏灯的电阻分别为:

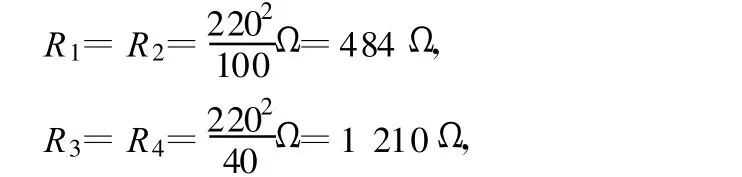
所以 R1=R2＜R3=R4.即 R4＞R1＞R23并.

因为串联电路 P∝R,所以 P4＞P1＞(P2+P3).而 L2与 L3并联,并联电路中所以 P2＞P3.

这4盏灯功率的关系是:P4＞P1＞P2＞P3,即灯 L3的实际功率最小,所以L3最暗,正确选项是(C).

2 利用不等式的定和求积模型

数学模型:如果两个正数的和一定,当两数相等时,其积最大.

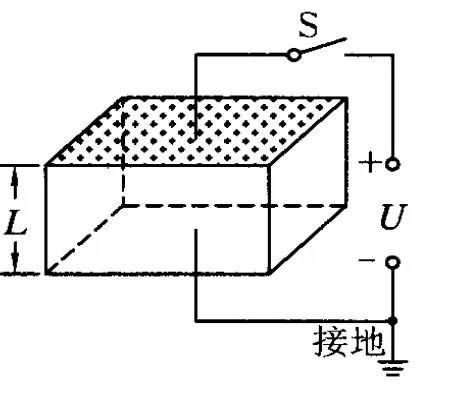
图2

例2.(2003年上海卷)为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积 A=0.04 m2的金属板,间距 L=0.05 m,当连接到U=2 500 V的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图2所示,现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒1013个,假设这些颗粒都处于静止状态,每个颗粒带电荷量为 q=+1.0×10-17C,质量为 m=2.0×10-15kg,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力.求合上电键后,

(1)经过多长时间烟尘颗粒可以被全部吸附?

(2)除尘过程中电场对烟尘颗粒共做了多少功?

(3)经过多长时间容器中烟尘颗粒的总动能达到最大?

解析:(1)当最靠近上表面的烟尘颗粒被吸附到下板时,烟尘就被全部吸附.烟尘颗粒受到的电场力

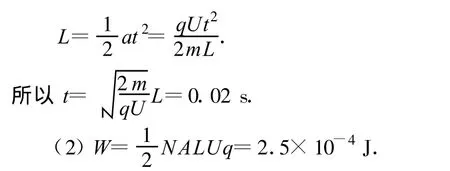
(3)设烟尘颗粒下落距离为 x,则

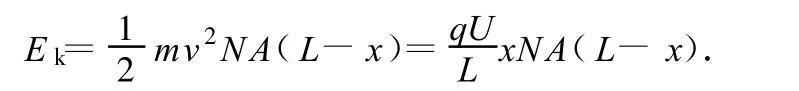
3 利用不等式的定积求和模型

数学模型:如果两个正数的乘积一定,当两数相等时,其和最小.

例3.如图3所示,一平直的传送带以速度v=2 m/s做匀速运动,传送带把 A处的工件运送到B处,A、B相距l=10 m.在A处把工件无初速地放到传送带上,经过时间t=6 s,能传送到B处.现调整传送带的运行速度,以使工件从A处传送到B处的时间最短,求传送带的运行速度至少为多大?

图3

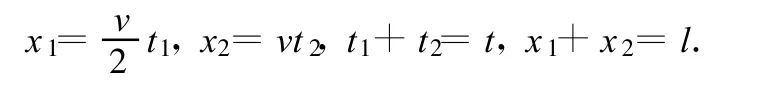
解上述4式得

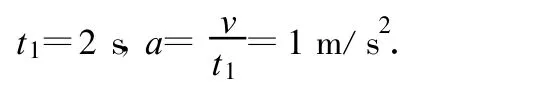
若要工件最短时间传送到B,工件加速度仍为a,设传送带速度为v,工作先加速后匀速,同理有又因为所以化简得因为常量,所以当即时,t有最小值,.表明工件一直加速到B所用时间最短.

4 利用不等式的降幂模型

数学模型:若 an＞bn且a、b为正数,n为正整数,则 a＞b.

例4.物体沿一直线运动,在 t时间内通过的路程为x,它在中间位置处的速度为v1,在中间时刻的速度为v2,则 v1和 v2的关系为

(A)当物体做匀加速直线运动时,v1＞v2.

(B)当物体做匀减速直线运动时,v1＞v2.

(C)当物体做匀速直线运动时,v1=v2.

(D)当物体做匀减速直线运动时,v1＜v2.

解析:利用公式比较.设这段过程的初速为v0,末速度为vt,则由匀变速直线运动的规律知所以当 v0=vt时取“=”号,当 v0≠vt时,有 v1＜v2,所以正确选项为(A)、(B)、(C).

5 利用不等式的“三均值模型”

例5.一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速度的释放,如图4所示,小球在运动至轻绳达到竖直位置的过程中,小球所受重力的瞬时功率在何处具有最大值?

图4

解析:当小球运动到绳与竖直方向成θ角的C时,重力的功率为

小球从水平位置到图中C位置时,机械能守恒有

解(1)、(2)式可得

令 y=cosθ sin2θ,因为.又因为