引 入 惯 性 力 场——处理加速系统中的浮力问题
倪红飞
(江苏省太仓市教研室,江苏太仓 215400)
1 问题的提出
例1.做匀速直线运动的小车上水平放置一密闭的装水的瓶子,瓶内有一软木塞,如图1所示,当小车突然向右加速时,软木塞相对于瓶子怎样运动?
这个问题已有多次讨论,常见的方法是根据牛顿运动定律求解,分析如下:
当小车突然向右加速时,瓶子中的水由于向右加速,在垂直于加速度方向的竖直平面的水层之间的压力发生了变化,而且左侧的水面间的挤压力较大,右侧水面间的挤压力较小,所以在软木塞的左右两侧产生了一个压力差.

图1

图2
对水平方向一段水柱进行分析(如图2),水柱向右加速时,左右两侧产生了一个压力差提供了水柱向右加速需要的外力,即

水柱左右两侧一个压强差为

此时,软木塞左右两侧一个压力差为
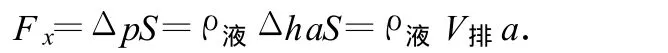
对软木塞应用牛顿运动定律:Fx=m′a′,即 ρ液V排a=ρ木V排a′,因为 ρ液>ρ木,所以,a′>a,软木塞相对于瓶子向右加速.
引入惯性力场解决这个问题,则更加思路简洁,而且分析过程更加体现理性思维的美感.
当小车突然向右加速时,以加速系统为参考系,系统水平方向存在着惯性力场,惯性力场a惯的方向与加速度方向相反,大小与加速度相等.
此时,水平方向受到两个力的作用,向左的惯性力F惯=ρ木Va和向右的浮力F浮x=ρ液Va(F浮x的方向与加速度的方向一致,大小为同体积水的惯性力的大小).由于液体的密度大于软木塞的密度,所以在水平方向软木塞受到的向右浮力F浮x=ρ液Va大于向左的惯性力F惯=ρ木Va,软木塞相对于瓶子将向右做加速运动.
2 加速系统中浮力问题的实例分析
2.1 竖直加速系统中的浮力问题
例2.如图3,一个盛水容器底部固定着一根弹簧,弹簧的上端连接着一质量为 m的木块,开始时,弹簧处于伸长状态,当容器向上加速时,弹簧的长度将如何变化?
对这个题目,如果直接用牛顿运动定律分析,求解烦琐且不得要领.引入惯性力场,说理特别简明.

图3

图4
如图4,系统静止时,根据木块平衡有

弹簧开始时的伸长为

系统加速向上时,以加速系统为参考系,则物体视重增加的同时,浮力也等比例增加.所以,弹簧的伸长变为

所以,弹簧的伸长增大.

图5

图6
2.2 水平加速系统中的浮力问题
例3.如图5所示,一容器中装满了水,在容器的底部和顶部分别用细线悬挂着木球B和金属小球A,当容器以加速度a向右做加速运动时.
(1)A、B两球分别向哪边摆动?
(2)细线与竖直方向的夹角为多少?
(3)连接A、B两球的细线受到的拉力分别为多少?
当容器向右加速时,以向右加速的系统为参照系,则在这个系统中同时存在向下的重力场g和水平向左的惯性力场a惯,合力场的方向 a合斜向左下方(如图 6),大小为a合=(如果采用类比的思想,这里的合力场a合相当于等效重力场).
此时,在垂直a合方向的同一平面内液体产生的压强相等,而沿a合方向压强不断增大Δp=ρ液a合Δh.因此,浸在液体中的物体受到的周围液体作用的压力差——即F浮方向与a合方向相反,大小为 F浮=ρ液a合V.公式中的 a合为重力场强度g、惯性力场强度a惯的矢量和.
由于木球B受到的浮力大于其重力与惯性力的合力,木球仍然“上浮”,故向前偏.铁球 A受到的浮力小于其重力与惯性力的合力,铁球仍然“下沉”,故向后偏.此时,细线与竖直方向的夹角为.两细线受到的拉力分别为

2.3 旋转系统中的浮力问题

图7
例4.在航天飞船上,如图7所示,有一长度为 l=20 cm的圆筒,绕着与筒的长度方向垂直的轴线OC以恒定的转速n=100 r/min旋转.筒的近轴端离开轴线OC的距离为d=10 cm,筒内装有非常黏稠的、密度为 ρ=1.2 g/cm3的液体.有一质量为 1 mg的密度为ρ′=1.5 g/cm3的粒子从圆筒的正中央释放(释放时粒子相对于圆静止),试求:该粒子在到达筒端过程中克服液体的黏滞阻力所做的功.若粒子的密度为 ρ″=1.0 g/cm3,其他条件不变,则粒子在到达筒端过程中克服液体的黏滞阻力所做的功又为多少?
这是全国物理竞赛的复赛题,原标准答案的解释学生很不容易理解,引入惯性力场后,问题的理解变得非常清晰.
在旋转系统中,液体中的各点的加速度都指向圆心,所以,粒子在运动过程中每一位置受到的浮力都指向圆心,由于各处的向心加速度不同,运动过程中受到的浮力也在不断变化.

图8
根据题意,粒子的密度 ρ′为大于液体的密度ρ,所以粒子在每一点受到指向圆心的浮力小于粒子向外的惯性力,粒子将向外运动.又因为在粒子向外运动到达筒端过程中,由于液体的黏滞阻力非常大,所以,可认为粒子缓慢运动过程中相对于在旋转系统近似平衡(如图8所示),即

粒子受到水平向里的黏滞阻力为
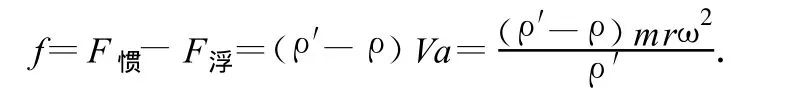

图9
由上式可知,f∝r,即与 r成线性关系,(如图9)粒子由筒中央到筒右端的过程中克服黏滞阻力做的功为直线下的面积,即
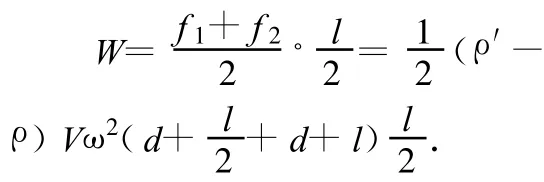
解得

当粒子 ρ″小于液体密度ρ时,同理可得


