集装箱多式联运协调计划的分级优化

靳志宏，兰 辉，2，孙 威，李 娜

(1.大连海事大学交通运输管理学院，辽宁大连 116026;2.大连港集团集益物流有限公司，辽宁大连 116004;3.大连海事局船舶交通管理中心，辽宁大连 116001)

0 引言

集装箱作为现代货物运输的主要载体，具有装卸效率高、运输方式适应性强、货差及货损率低以及便于管理等优势，适应全球经济一体化对于运输发展的要求，在全球运输领域得以迅速发展.近20年来，世界集装箱港口吞吐量以每年10%左右的速度增长，2006年我国集装箱吞吐量达到9 300万TEU，连续4年居世界首位.

集装箱多式联运是集装箱运输发展的高级组织形式，以集装箱为媒介，将海路、铁路、公路、内河水路以及航空等多种运输方式有机结合，构成连续、综合的一体化货物运输网络，为客户提供经济、合理、便捷的运输服务，更好地实现“门到门”的运输.集装箱多式联运系统由枢纽港、中转港、内陆集装箱场站和内陆办理站等众多节点以及海路、铁路、公路、航空和内河水路运输等众多弧组成.由于集装箱多式联运涉及的节点和中转环节多，要求各种运输方式之间以及参与多式联运的企业之间相互协同合作，才能缩短集装箱的周转时间，提高集装箱利用率，达到联运的全程系统优化，实现多式联运的综合效益.因此，对集装箱多式联运系统的协调管理提出更高的要求.［1]

鉴于多式联运在集装箱运输方面的重要地位，国内外专家已对此进行大量研究.孙家庆［2]对我国现阶段多式联运的形式及其特征进行分析与比较;魏际刚等［3-4]论述集装箱多式联运系统的宏观布局协调、能力协调和组织经营协调等7个方面的协调问题，并提出一些相应原则;马彩雯等［5]分析多式联运组织的特征，认为其运作符合虚拟企业的特点，可运用虚拟企业的运作模式解决多式联运参与各方的协作问题;廖日卿［6]提出构建集装箱多式联运虚拟企业，根据具体的运输任务将承运人企业和各个运输企业最大的优势动态地组合，使集装箱多式联运组织的整体力量远大于参与各方单个力量的简单之和.

在集装箱多式联运协调管理的定量研究方面，BOSTEL等［7]建立集装箱海—铁联运堆场的作业优化问题模型，减少集装箱在港口的不必要移动，并提出优化算法;KIM等［8]探讨快件运输的航空—公路联运优化问题，并考虑服务时间窗口等现实约束条件，为大规模快递服务网络的设计决策提供参考;KOZAN［9]探讨影响多式联运效率的相关因素，并提出1个集装箱码头的网络模型，可为多式联运提供决策支持;JANSEN等［10]提出1个基于港口的集装箱运作计划的模拟研究，其成果已应用于日常集装箱的调度计划;靳志宏等［11]探讨集装箱多式联运系统装卸与运输一体化优化问题;曾庆成等［12]针对集装箱码头内机械的协调调度问题进行定量分析;靳志宏等［13]定量分析集装箱多式联运系统拼箱集运优化问题.

上述定量研究基本局限于多式联运网络中的某个节点或某个弧的调度协调.本文从集装箱多式联运的组织者(多式联运经营人)的角度，针对多式联运协同基础的计划协调问题，在分析多式联运计划层次的基础上，建立多式联运计划的分级优化概念模型，并针对模型中的核心内容——海上班轮运输计划和内陆集疏运计划进一步建立任务分配的优化模型，通过分析该类问题的结构特征，设计相应的遗传算法对优化模型进行求解.

1 多式联运计划特点和分级优化概念模型

1.1 多式联运计划的特点

多式联运计划是多式联运经营人根据市场需求和多式联运组织的协同管理情况制订的整个集装箱运输网络的运输计划.与原有的单一运输方式的运输计划相比增添许多新特点:

(1)集成性.包括纵向集成与横向集成，纵向集成指多式联运计划中由下游向上游的信息集成;横向集成指各参与方之间的信息共享.

(2)层次性.多式联运计划涉及货主、货代、船代、班轮公司、港口、场站和运输企业等不同职能的自主实体以及运输的不同阶段.

(3)协调性.多式联运参与各方都为自主实体，需在一定规则下基于多式联运的整体利益进行协调.

(4)约束柔性.航运市场以及多式联运网络众多节点和弧段的运输承诺都动态变化，承诺及其柔性是多式联运合同签订的关键因素.

1.2 多式联运计划的分级优化概念模型

多式联运计划涉及班轮公司、场站、码头和堆场等众多节点以及公路、铁路和水路等众多弧段，计划过程中众多变量之间存在较强的耦合关系和时序约束，是个多目标、多约束、复杂的非线性优化问题，用传统的数学规划方法难以得出满意的结果.分级制订多式联运计划是个合理的选择，包括初步计划、海上班轮计划、内陆集疏运计划、场站计划和空箱调运计划.

2 多式联运计划分级优化建模

2.1 海上班轮运输计划优化建模

集装箱班轮运输计划任务的分配对象为各从事海上集装箱运输的班轮公司.在多式联运初步计划产生后，依据各航线的运量分布情况向经营各航线的班轮公司发出集装箱运输信息，各班轮公司根据自身航线的经营状况，向多式联运经营人提供该日的箱位供给量.根据初步计划和各班轮公司的运量供给信息，多式联运经营人对海上运输任务进行分配.多式联运承运人在进行计划任务分配时需考虑各航线的运输量、各班轮公司最大箱位供给量和完成集装箱海上运输的成本.图1为集装箱多式联运计划分级优化概念模型.

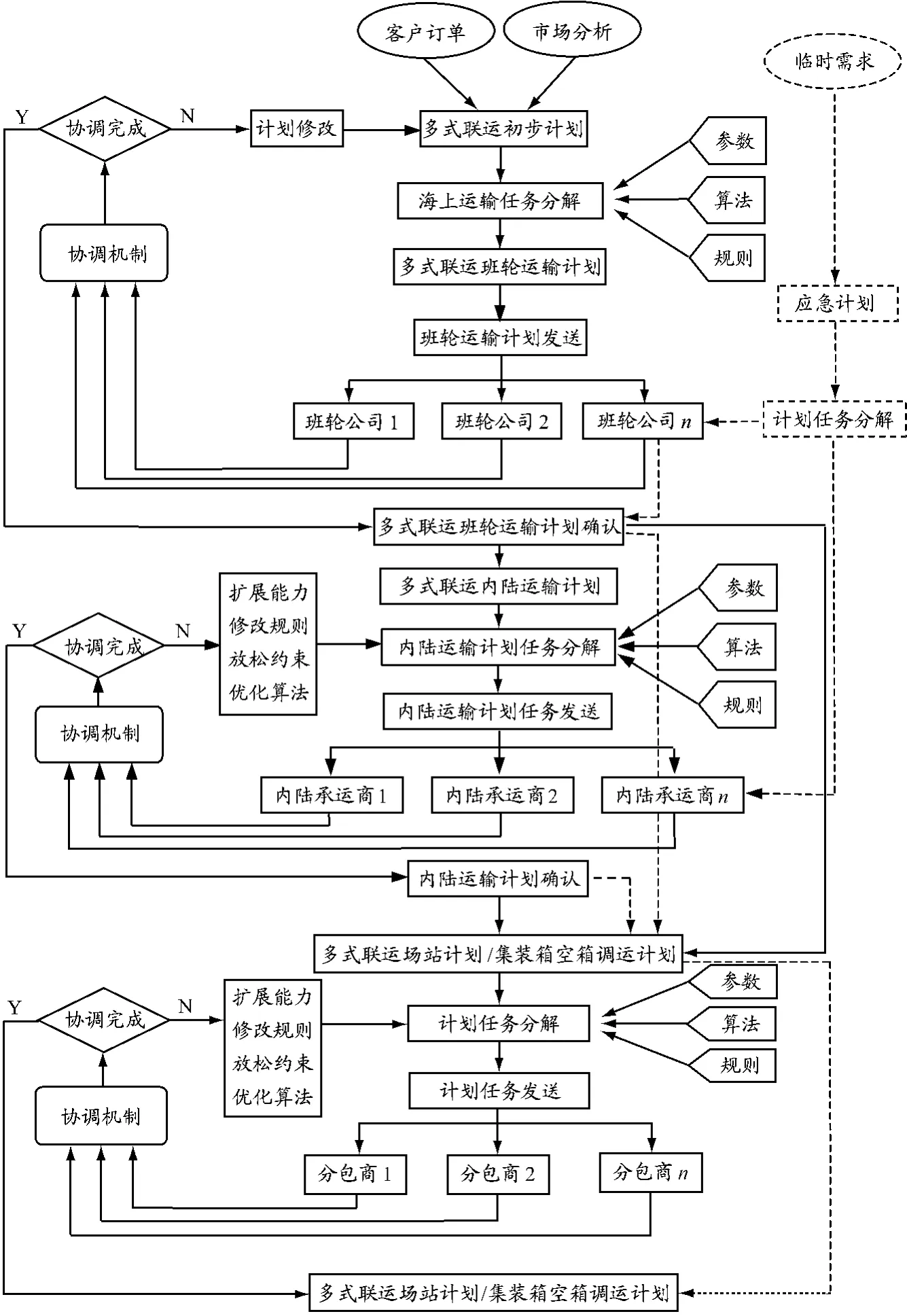
图1 集装箱多式联运计划分级优化概念模型

设共有n条航线和m个班轮公司参与多式联运，航线 i(i=1，2，…，n)的箱位需求量为 Ti(i=1，2，…，n)，各航线海上运输的成本上限为Ri(i=1，2，…，n)，班轮公司 j(j=1，2，…，m)在航线 i上的运输费用为rij，班轮公司j为航线i提供的箱位量为，tij和xij都为决策变量.

考虑到航运市场的特点，为规避风险，每个班轮公司参与多条航线的经营，每条航线由多家班轮公司共同运营.同时，当计划任务分配结果无法满足箱位需求量或超过航线费用成本约束，可对计划进行修改，与有富余能力的班轮公司进行运力协调，增加运输能力以满足初步计划.

由于箱位供给量tij属效益型指标，可通过下式对所有班轮公司在各航线上的箱位供给量进行规范化处理，

运输费用rij属于费用型指标，可通过下式对所有班轮公司在各航线上的运输费用进行规范化处理，

设目标权重因数分别为α和1－α，则班轮运输计划任务分配优化模型的目标函数为

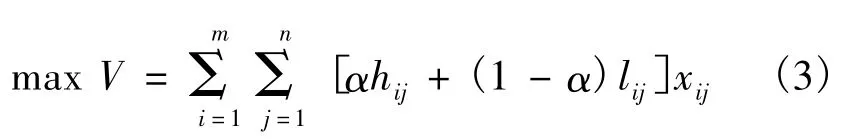
式中:前1项为各航线的班轮公司集中度尽量高，有利于取得运输的规模效益;后1项为费用型指标的倒数最大化目标.各航线的箱位系列需求约束为

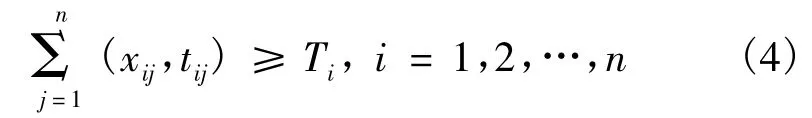
多式联运经营人的费用上限约束为

现实中，集装箱班轮运输计划任务的分配还存在软约束，为方便计划的制订和执行，同时也易于多式联运经营人协调运输过程，可使从事各航线经营的班轮公司只集中于几家而不过于分散.软约束可表示为

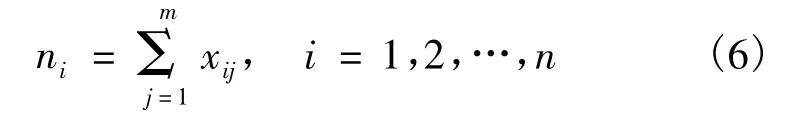
2.2 内陆集疏运计划优化建模

在班轮运输计划确定后，多式联运经营人针对各枢纽港及其相应的内陆经济腹地制订内陆运输计划.根据班轮运输计划和客户要求并考虑成本因素，多式联运经营人确定各腹地区域计划期内每日的内陆运输计划，并参照内陆运输企业的运输能力进行任务分配.

设有p个合作伙伴参与q个区域的运输，多式联运经营人对各区域的计划运输量Si(i=1，2，…，q)，第j个运输企业对第i个区域可提供的运输量最高为uij，同时考虑运输企业的经营成本，需设置其最低分配运量lij，即第j个运输企业对于第i个区域的运输量区间为［lij，uij].决策变量为多式联运经营人分配给第j个运输企业第i个区域的运输量yij.

多式联运经营人根据运输要求和运输路线的不同确定最适合的运输方式，如长距离、大批量的运输可采用铁路运输，小批量、短途运输可采用公路运输，从而设定各运输企业承运不同运输任务的适宜度，设第j个运输企业对第i个区域的运输适宜度为.另外，合作的不同运输企业由于规模、技术条件和管理水平的不同，多式联运经营人的评价也不同，设多式联运经营人对第j个运输企业的评价度为

设第j个运输企业从事第i个区域运输的正理想值为其上限值uij，负理想值为其下限值lij，则第j个运输企业的正理想方案与多式联运经营人的最优配置方案间的加权欧氏距离平方为

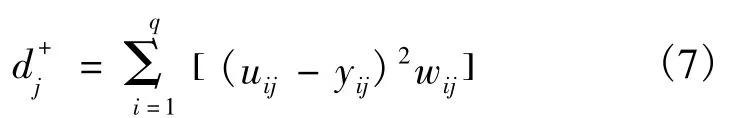
所有运输企业的正理想方案与最优配置方案之间距离的加权和为

负理想方案与最优配置方案之间的加权欧氏距离分别为

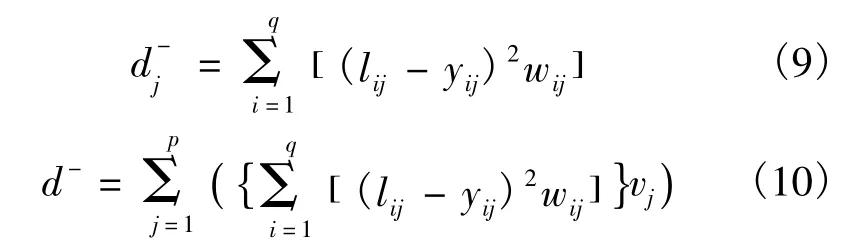
可知，最优配置方案越接近正理想方案，运输企业满意度越高，即d+越小越好;最优配置方案越远离负理想方案，运输企业满意度越高，即d－越大越好.最优方案的综合满意度为

内陆集疏运计划的优化目标函数为

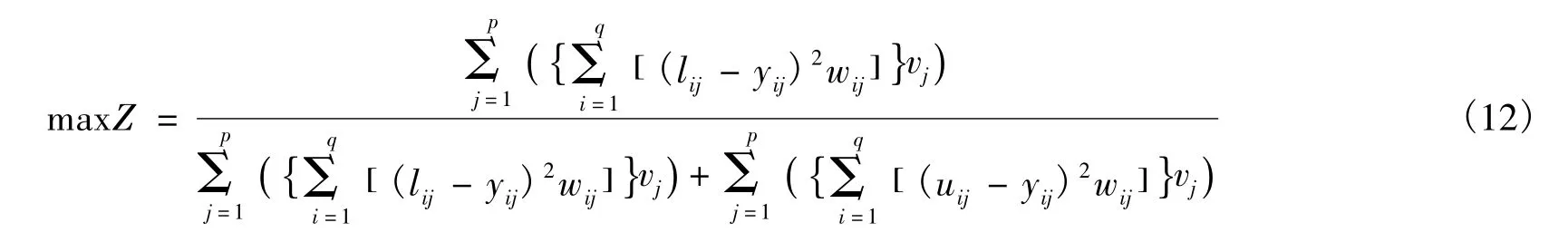
各运输企业及各腹地区域的运输量约束分别为

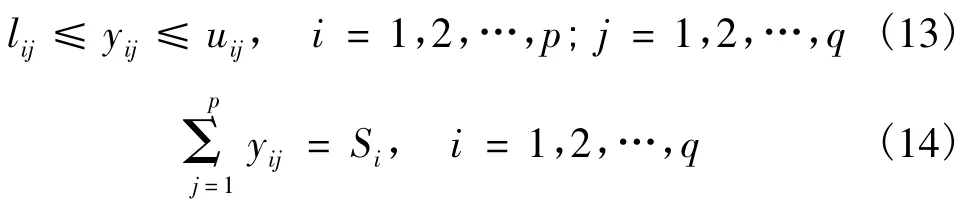
3 多式联运计划分级优化算法设计

由模型特点可知，海上班轮运输计划分配可采用二进制编码，内陆集疏运计划分配可采用十进制编码.利用遗传算法对2种进制均可以编码的特点，对模型分别作算法设计.

(1)编码设计.选择二进制编码表示班轮公司任务分配的解，每种任务分配结果可用图2所示的代码串表示，每个字段表示每个合作伙伴的任务分配状态;选择十进制编码表示内陆集疏运计划中合作运输企业分配的任务解，每种任务分配结果可用图3所示的代码串表示，每个字段表示每个合作伙伴的任务分配状态.

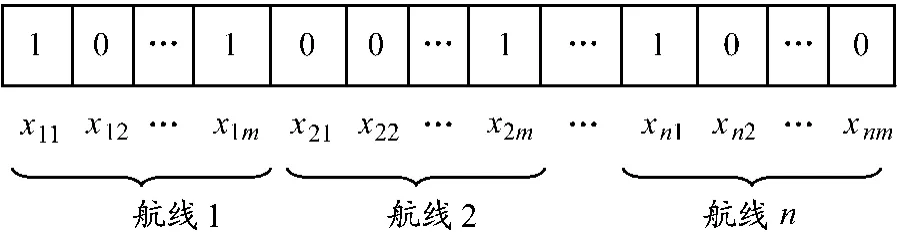
图2 海上班轮运输计划分配算法编码示意

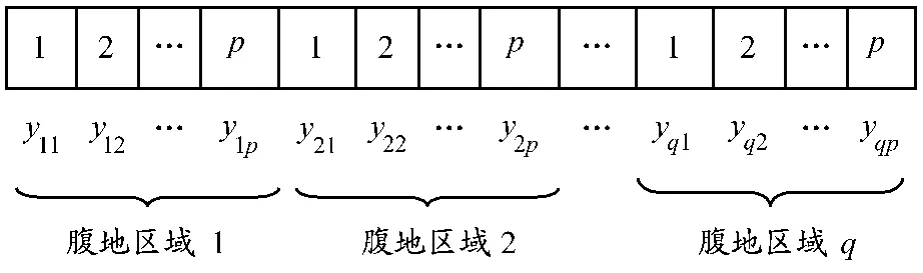
图3 内陆集疏运计划分配算法编码示意

(2)生成初始群体.从满足约束条件的可行域中随机挑选L个初始可行解，构成初始群体.

(3)构造适应度函数.通过对不可行解进行惩罚，将有约束问题转化为无约束问题.海上班轮运输计划分配算法的惩罚函数为

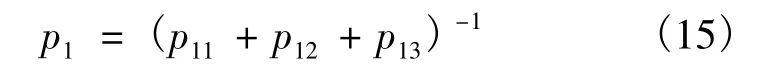
式中:p1i(i=1，2，3)分别针对式(4) ～(6):

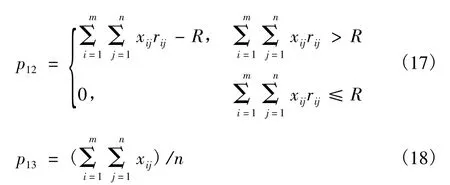
结合式(3)和(15)，得海上班轮运输计划的适应度函数

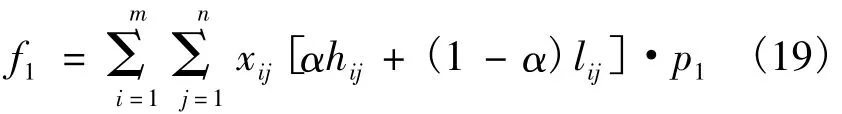
内陆集疏运计划分配算法的惩罚函数为

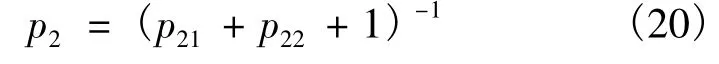
式中:P2i(i=1，2)分别针对式(13)和(14):

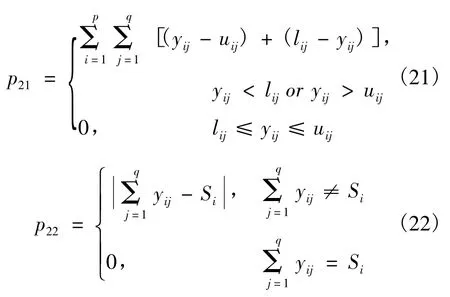
结合式(12)和(20)，得内陆集疏运计划适应度函数

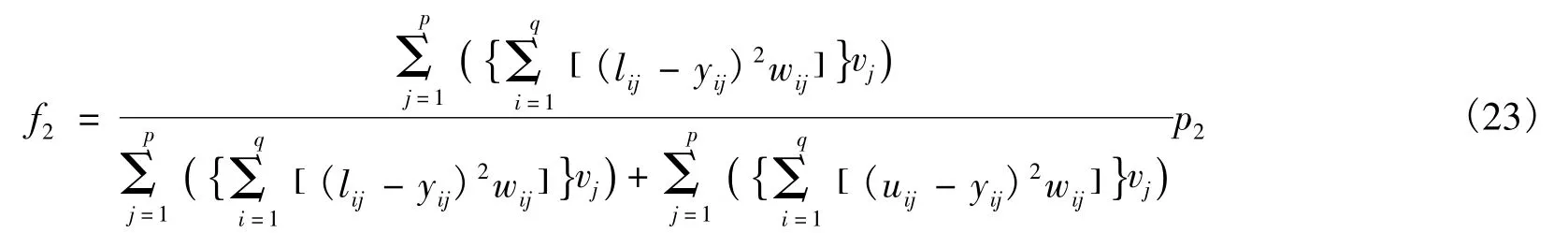
(4)选择算子.海上班轮运输计划及内陆集疏运计划均采用线性排序，将适应度函数值转换为适应度序列值

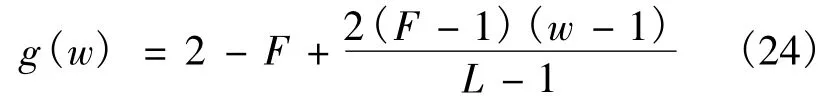
式中:w为个体在种群中的序位;F为选择压力参数.分别采用比例选择以及赌盘选择法(roulette wheel selection)对个体进行选择.

(5)交叉算子和变异算子.采用单点交叉对个体进行交叉操作，交叉概率 pc=0.5，变异概率pm=0.01.

4 仿真试验分析

4.1 海上班轮运输计划仿真试验

目前，在本地区航运市场上主要有5家班轮公司从事6条集装箱航线的运输，在某个计划期内，多式联运经营人允许的费用支出上限为400万元.各班轮公司可向多式联运经营人提供的集装箱箱位量见表1，各班轮公司在各航线上运输所需的费用见表2，对箱位供给量数据进行规范化处理结果见表3，对班轮公司在各航线上的费用成本规范化处理结果见表4，任务分配综合优化模型中箱位量和费用指标的权重分别取0.5，箱量分配的综合数据见表5.

表1 各班轮公司提供的集装箱箱位量 TEU

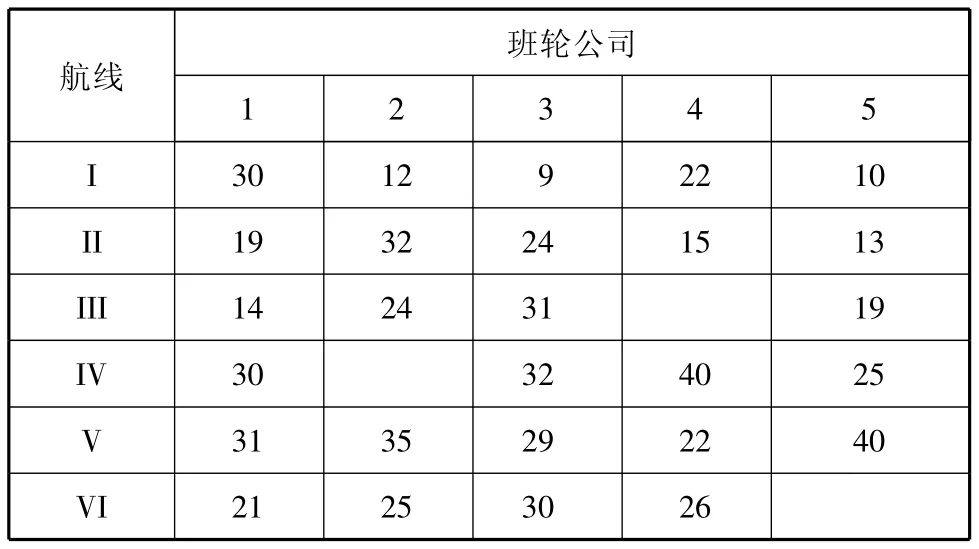
表2 各班轮公司集装箱海上运输费用 万元

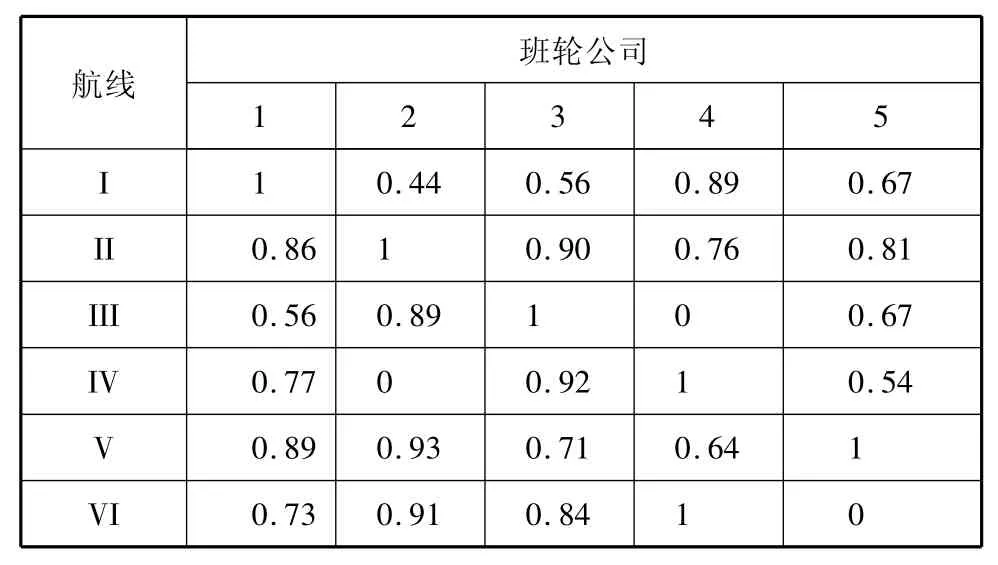
表3 箱位供给量规范化处理结果

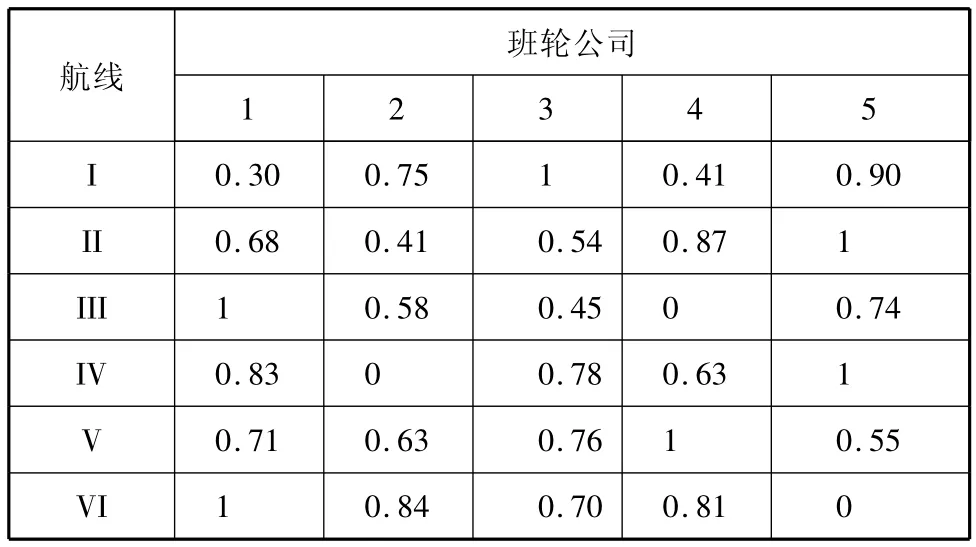
表4 费用成本规范化处理结果

表5 箱量分配的综合数据

用遗传算法求解，设迭代代数为200，种群规模为30.用Matlab 7编程，经过200次模拟后得任务的最优分配目标函数为3.5063，总费用为383，满足多式联运经营人本计划其费用约束条件.任务的分配结果见表6，各航线集装箱供给量见表7.

表6 班轮公司各航线分配决策变量

表7 各航线集装箱供给量 TEU

4.2 内陆集疏运计划仿真实验

某枢纽港在其内陆腹地区域共有5条主要的集疏运线路，在某个计划期内进口集装箱为85 TEU，该批集装箱在内陆集疏运线路的分布见表8，参与该区域运输的5家班轮公司在计划期内可提供的最高运力见表9.

表8 计划期内进口集装箱在内陆集疏运线路的分布情况

表9 计划期内各班轮公司可提供的最高运力 TEU

各班轮公司为维持其经营活动，需要有一定的运输业务保证其有足够的收入以抵消成本支出，其最低运输任务量见表10.各班轮公司对不同路线的运输适宜度见表11，多式联运经营人对各班轮公司的评价度见表12.

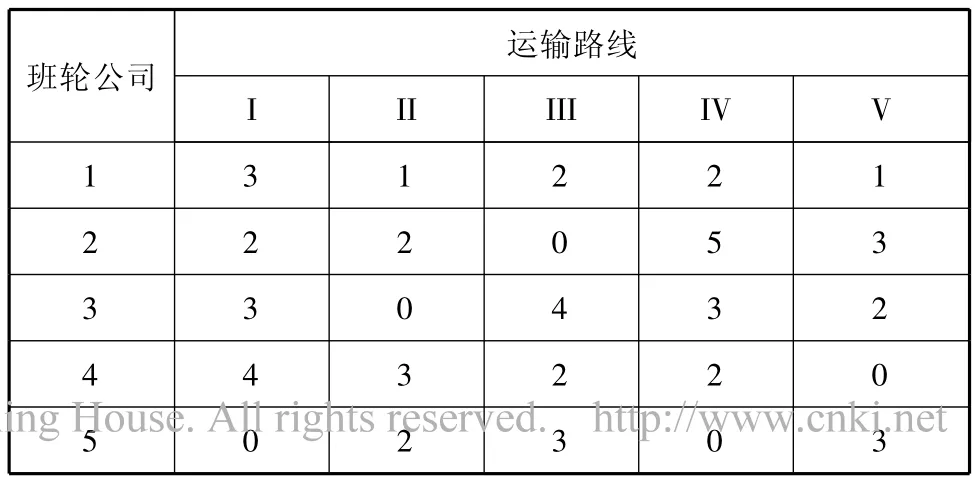
表10 计划期内各班轮公司的最低运输量 TEU

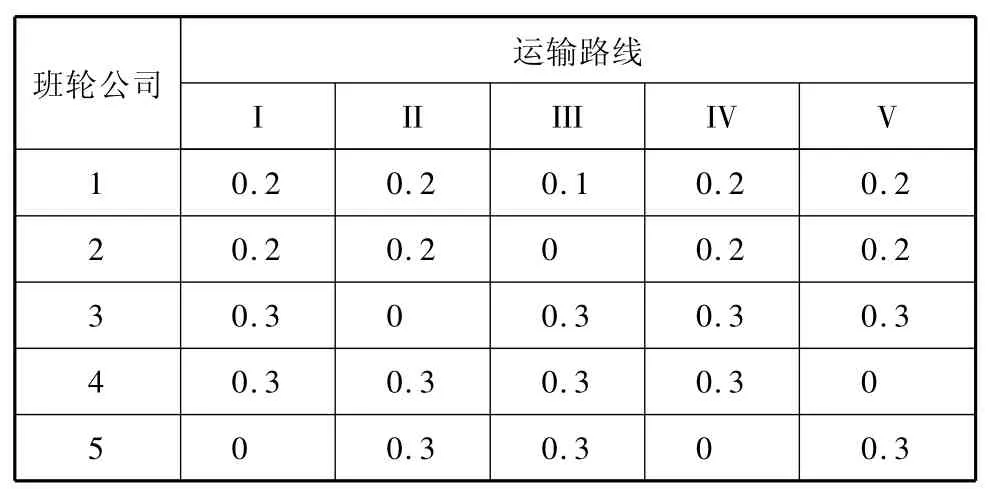
表11 各班轮公司在各集疏运线路上的运输适宜度评价值

表12 对各班轮公司的评价度

遗传算法优化过程见图4.

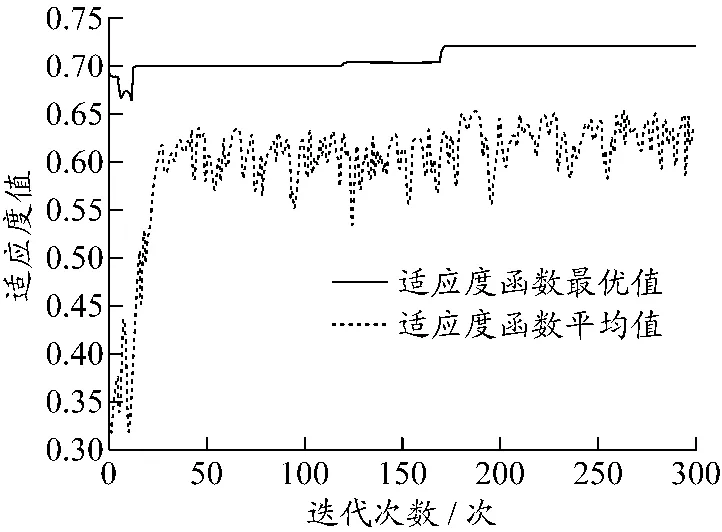
图4 遗传算法优化过程

由图4可知，在迭代160次后，目标函数值趋于稳定，最优函数值为 0.719 7，任务分配结果见表13.

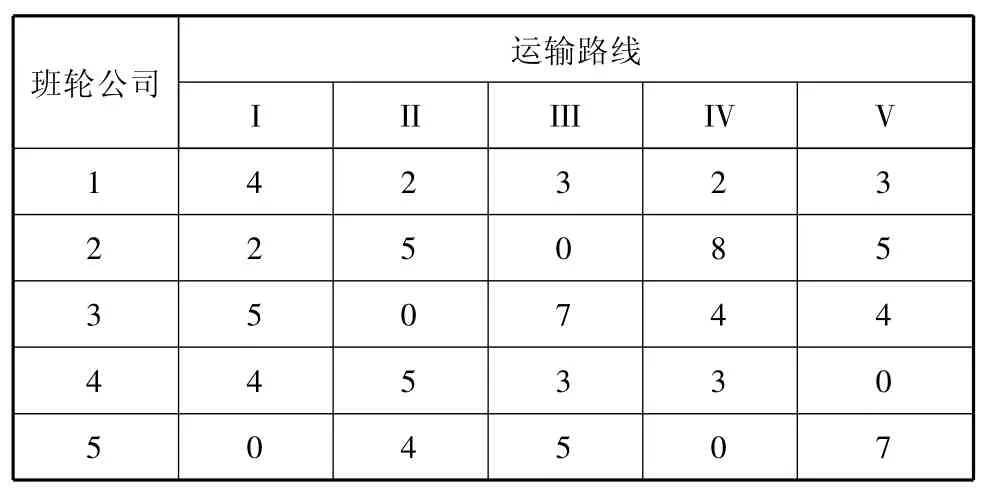
表13 运输任务分配结果

多式联运经营人将上述运输计划任务分配结果发送给各内陆运输企业，内陆运输企业在内部对任务进行平衡，并将结果反馈给多式联运经营人.根据反馈结果，最终确定计划期的多式联运内陆集疏运计划，并据此进一步制订场站和空箱调运计划.

5 结论

多式联运计划是多式联运经营人对运输过程进行组织和控制的重要手段.本文针对多式联运计划的层次性特点，提出分级优化的优化思路，建立海上班轮运输和内陆集疏运的任务分配优化模型，并设计相应的遗传算法对优化模型进行求解.通过试验证实模型与和算法的有效性及实用性.

多式联运协调计划是项复杂的系统工程，参与方多、牵涉面广.分级制订和优化处于多式联运系统不同环节的协调计划仅仅是第1步，今后的研究可在涉及不同环节之间、不同运输方式之间以及不同参与方之间的协调计划的集成方面展开，实现多式联运全程协调一致和全程一体化的优化调度.

［1]靳志宏.构筑集装箱多式联运通道，促进港口物流与区域物流协调发展［J].中国远洋航务公告，2006(2):33-34.

［2]孙家庆.多式联运的形式及其特征分析［J].集装箱化，2002，13(3):28-30.

［3]魏际刚，荣朝和.我国集装箱多式联运系统的协调问题(上)［J].集装箱化，2000，11(2):21-24.

［4]魏际刚，荣朝和.我国集装箱多式联运系统的协调问题(下)［J].集装箱化，2000，11(3):18-21.

［5]马彩雯，王志远，孙光圻.国际多式联运的虚拟企业运作模式研究［J].交通运输规划与管理，2004(4):18-23.

［6]廖日卿.集装箱多式联运虚拟企业初探［J].港口装卸，2006(1):37-39.

［7]BOSTEL N，PIERRE D.Models＆ algorithms for container allocation problems on trains in a rapid transshipment shunting yard［J].Transportation Sci，1998，32(4):370-379.

［8]KIM D，CYNTHIA B，KEITH W，et al.Multimodal express package delivery:a service network design application［J].Transportation Sci，1999，33(4):391-407.

［9]KOZAN E.Optimizing container transfers at multimodal terminals［J].Math ＆ Comput Modeling，2000，31(4):10-12.

［10]JANSEN B，SWINKELS P C J，TEEUWEN G J A，et al.Operational planning of a large-scale multi-modal transportation system［J].Eur J Operational Res，2004，156(1):41-53.

［11]靳志宏，朴惠淑，杨华龙.集装箱多式联运系统装卸与运输一体化优化问题［J].系统工程，2005，23(11):1-7.

［12]曾庆成，杨忠振，靳志宏.集装箱码头集卡调度优化模型与算法［J].系统工程，2006，24(S):187-190.

［13]靳志宏，计明军，朴惠淑.集装箱多式联运系统拼箱集运优化问题［J].系统工程，2007，25(S):71-74.