保险索赔数据的统计分析

赵 慧 ，荣喜民

（天津大学a.管理学院；b.理学院，天津 300072）

0 引言

目前，随着我国经济的发展，外资保险公司大举进入我国保险市场，国内保险业的竞争正愈演愈烈。保险公司要在竞争中求生存，除了加强管理和提供优质服务以外，还必须对保费确定、损失鉴定与赔偿等保险精算问题进行深入的研究。索赔数据是保险人最为关注的问题之一，由于其不确定性，保险公司必须保留一定责任准备金以备赔付，所以各类索赔金额直接关系保险公司财务运营的稳定性。

关于保险索赔额的研究已有不少成果。韩天雄，蒋华华（1997）提出了索赔额的分布拟合，修正了传统的索赔额分布拟合函数。徐小阳，李光久（2004）在韩天雄等（1997）基础上针对实例对索赔额的理论分布进行了适当修正，使得分布函数既对小额损失有确切估计，又对巨损危险有所考虑，从而对高额赔款损失能有较为准确的描述。其中具有重尾分布函数的索赔对保险公司影响巨大，一直是索赔额研究的热点。欧阳资生（2007）提出了巨灾保险索赔数据的极值风险度量。Rolski（1998）等利用Q-Q图方法分别研究了工业事故、工业火灾和车险索赔额的分布，此方法可以由实际数据拟合出索赔额分布，但需要与理论分布相比较才可得到结果。对于单纯检验分布重尾性的问题，其实证实现较为复杂。然而，现今从索赔数据角度研究保险公司的文献还较少，基于我国保险公司索赔额的实证分析几乎没有。所以本文主要基于不同保险公司各类财产险的索赔数据进行统计分析。

1 因子分析

1.1 数据来源和研究方法

本研究以国研网金融数据库财产保险分公司2006年业务统计表为依据，选取国内31个省、市、自治区的361家财产保险分公司的索赔数据进行分析。部分数据列于表1。

财产保险公司将其承保险种分为9类，如表1所示。这9类索赔可看作是保险公司索赔额的9个指标，这些指标间具有潜在的相关性，所以可以将其综合为少数几个影响因素，简化对索赔数据的分析。在361家财产保险分公司中，一些保险公司只经营9类保险中的部分业务，所以样本中有较多缺省数据和0。为减少样本差距对指标分类的影响，将含0较多和含缺省值的样本剔除，精选139个样本，应用统计分析软件R2.7.2作因子分析。

1.2 数据分析与结果说明

首先利用主成分分析方法确定财产险索赔指标的潜在因子个数。主成分分析是一种通过降维技术把多个变量化成少数几个能反映原始变量绝大部分信息的主成分的统计分析方法，这些主成分通常表示为原始变量的线性组合。

对索赔数据的相关系数矩阵作分析，得到前三个主成分的累积贡献率已达72.427%，说明前三个主成分已可以反映原始9个指标的大部分信息。所以提取三个因子对9类财产险作因子分析。为了清楚解释该三类因子的构成，对因子载荷矩阵进行方差最大化旋转，得旋转矩阵如表2。

由表2中因子载荷的大小，可以把保险公司财产险的索赔归结为三类影响因素。 因子 1（F1）主要与x1，x4和 x9正相关，除农业保险指标x6外，该因子与其他指标均正相关，因此认为第一个因子为工业财产险因子。因子2（F2）主要包含了机动车辆保险（x2）、意外伤害保险 （x8）、 信用保证保险（x5）和企业财产保险（x1）几个险种的信息，是反映大额索赔保险的因子。 因子 3（F3）是特殊财产险因子，包含短期健康险和农业保险这两类财产险中特殊指标的内容。从以上分析可得，财产保险公司的总索赔额与9个险种有关，这9类影响因素又可归结为3个因子，按影响的大小将3个因子排序为F1、F2和F3。由R软件计算出各样本的因子得分，分别求出各因子的平均得分，如表3所示。

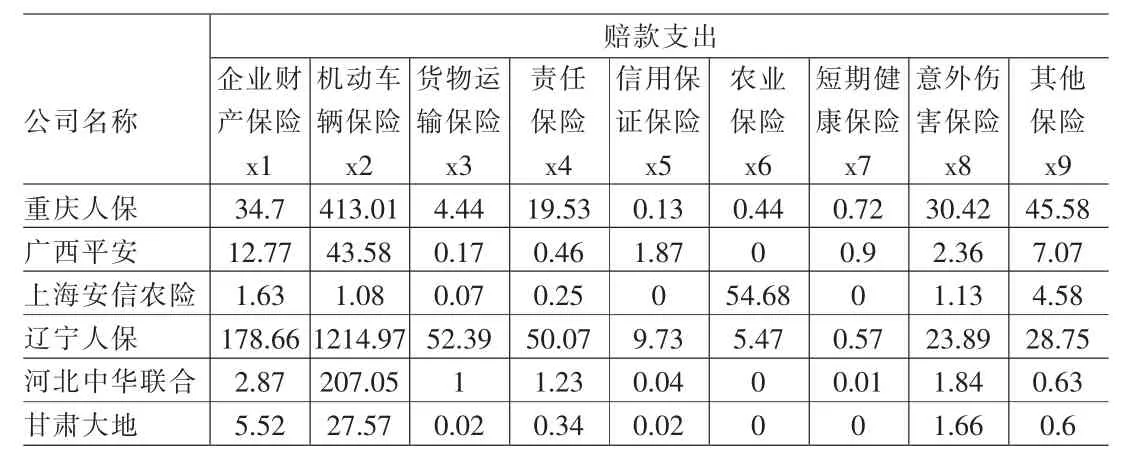
表1 2006年各财产保险分公司业务统计表 （单位：人民币百万元）

表2 因子载荷矩阵

表3 因子得分平均值

通过与因子得分的平均值作比较，可以分析每家保险公司在3类综合险种上的索赔额是否偏大，指导保险公司的业务分配。例如重庆人保公司其因子1的得分远远大于平均值，而因子3的得分小于平均值，说明该公司在工业保险方面的索赔较多，索赔金额较大，而在农业保险等小额保险上的索赔并不多，所以可以适当增加在农业保险和短期健康险方面的业务。

根据各因子方差贡献率，以表2给出的各因子权重构造保险公司财产险索赔额综合得分的计算公式如下：

将各因子的平均得分带入公式，得到财产险索赔额的平均综合得分为0.00379。利用平均W值可以建立财产保险公司的索赔预警指标。由标准化后的原始数据计算每家保险公司的W值，若其值大于0.00379，则说明该公司的索赔额较多，该公司可通过增加保险业务或拓展新业务，如利用保费进行投资等途径弥补索赔带来的损失。

2 财产保险公司分类

由各险种的索赔数据可以看出不同保险分公司之间的索赔额差距明显，采用我国财产保险分公司2006年业务统计表中的索赔数据对全国361家财产保险分公司利用K-均值法进行动态聚类，可分为以下12类。(1)重庆人保、广西人保、广东太保、河南人保、上海东京海上、山西人保、内蒙人保、吉林人保、黑龙江人保、浙江太保、浙江中华联合、山东太保、江西人保、安徽人保、甘肃人保、青海人保、贵州人保、新疆人保、甘肃平安、陕西人保、云南人保、四川人保、四川华安；(2)广东人保；(3)广东平安、湖南平安、广东联合、天津平安、浙江平安、江苏中华联合、江苏大众、江苏平安、福建平安、安徽平安、四川中华联合、四川大地、河北平安；(4)广东太平；(5)广东信保、河南信保、天津信保、北京平安、江苏信保、浙江信保、辽宁平安；(6)湖南人保、湖北人保、天津人保、上海太保、上海人保、辽宁人保、河北人保、北京人保、江苏太保、福建人保；(7)新疆中华联合、黑龙江阳光农业；(8)上海平安；(9)浙江人保、山东人保、江苏人保；(10)四川太平；(11)贵州安邦；(12)其余公司。

从以上聚类结果可以看出，各保险分公司主要呈现出按公司和按地区聚类的特点。

（1）298家保险分公司聚为(12)类，说明大部分财产保险分公司的索赔结构类似，便于保监会统一管理。而各地人保分公司基本都没有在(12)类里，由索赔数据也可看出，人保公司的索赔业务遍及各类财产险，索赔额相对其他分公司较大。说明人保公司在财产保险方面较其他保险公司承保业务全面，承保量大。

（2）人保公司、平安保险及信保公司分别各自聚为一类。广东信保、河南信保等5家信保保险公司与北京平安、辽宁平安公司聚为(5)类，这几家公司的信用保证保险在财产险索赔总额中占很大比重，几家信保公司只有信用保证保险的索赔，同时索赔数额也很大。而对其他大部分公司而言，信用保证保险不是主要业务。广东、湖南、天津等地的平安保险聚为(3)类。而(1)类、(6)类和(9)类主要由人保分公司组成。

（3）对人保公司，聚类结果有一定的区域特征。黑龙江、重庆、安徽、青海、新疆等地的人保分公司聚为一类，可认为我国内陆地区的人保公司索赔特点相近。北京、河北、湖南、上海、天津、福建等地的人保分公司聚为(6)类，表明部分沿海地区和京津冀地区的人保分公司索赔结构类似。浙江、江苏两省相邻，其人保分公司据索赔业务也组为一类。

（4）广东人保、广东太平两家保险公司各自成一类。由统计数据也可看出这两家公司保险业务全面，索赔数额较大，特别是企业财产险和机动车辆险这两类大额索赔保险。另外广东地区的保险公司在前11类中出现频率高，说明广东省保险公司的索赔具有其地区特点，可以单独监管。

（5）贵州安邦、四川太平各自为一类。

3 部分险种赔付额分布的重尾性检验

3.1 经验剩余风险均数[4]

设非负随机变量X的分布函数是F(x)，令

易知 μF(t)=E[(X-t)｜X>t]，所以称 μF(t)是剩余风险均数。 由剩余风险均数μF(t)可以给出重尾分布的一个充分条件。

引理1：分布F的剩余风险均数是μF(x)，当x→∞时，如果μF(x)→∞，则F是重尾分布。

根据统计数据判断某类保险索赔额的分布F是否是重尾分布时，需要引进经验风险均数的概念。令{Ui，1≤i≤n}为一类保险的一系列索赔额，将其排序，得到U1，…，Un的顺序统计量

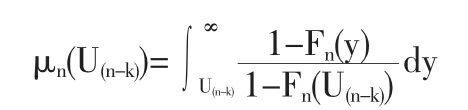
将（2）式带入上式化简得[4]：

据引理1，如索赔额的分布F是重尾的，则当n→∞时，F的经验剩余风险均数μn(U(n-k))→∞。

3.2 实证检验

对于一类保险的索赔数据，现将其按升序排序，按上文所述选择 k。 取 1≤j≤k，以索赔额 U(n-j)为横坐标，μn(U(n-j))为纵坐标作图，以索赔额分布的经验剩余风险均数的图像近似剩余风险均数图像。当图像显示μF(x)的趋势是随着x的增大趋于无穷大时，就认为此类保险的赔付额分布是重尾的。下面通过四组实例具体说明。

（1）采用《中国保险年鉴》中我国各省市保险分公司2002～2006年有记录的245例工业火灾索赔额的数据，应用R2.7.2编程作出工业火灾险赔付额分布的经验剩余风险均数图像，见图1。由其图像，可以认为工业火灾索赔额的分布是重尾分布。因此，对于工业火灾险以及易出现火灾的公司（如造纸厂等）的财产综合险、企业财产险等的索赔额，可用重尾分布函数拟合。

（2）选取某保险公司家庭火灾险容量为100的赔款额样本[1]，具体数据见参考文献[2]，取赔付额区间的组中值作为赔款额。编程作出此类保险的赔付额分布的经验剩余风险均数图像，见图2。由图像可知，经验风险剩余均数波动较大，不呈趋于无穷大的趋势，所以可以认为家庭火灾险的索赔额分布不是重尾的，进而可用轻尾的分布函数拟合此类保险的索赔额。

（3）选取我国2002～2005年洪水灾害造成的损失数据作为洪灾保险索赔数据的模拟，数据取自 《中国水利年鉴》。2002至2005年我国每年都发生多起洪灾，以每起洪灾造成的经济损失作为赔付额，样本容量是80，部分具体数据略。作出赔付额分布的剩余风险均数图，如图3所示，可以认为洪灾索赔额的分布是重尾分布。因此采用重尾分布函数拟合洪水等自然灾害造成的索赔额的分布是合理的。

图1 工业火灾索赔额剩余风险均数

图2 家庭火灾索赔额剩余风险均数

图3 洪灾索赔额剩余风险均数

图4 地震索赔额剩余风险均数

（4）选取1966～1990年我国有经济损失统计的35次地震的经济损失数据作为震灾索赔额的模拟，数据取自《中国震例》和《中国地震年鉴》，部分列于附录。图4是地震保险索赔额的经验剩余风险均数图，易见地震险索赔额的分布是重尾分布，进一步验证了巨灾保险索赔额服从重尾分布的题设。

索赔额具有重尾分布的险种一般是那些发生概率很小但又对保险业造成重大影响的巨灾保险，由其特点，很难设计保费费率，一家保险公司也难以承担其巨大风险。因此巨灾险设计需要政府等多方支持。保费可设计为限额赔付保险形式，损失在限额以下保险公司予以赔付，限额以上部分则通过补充性的商业保险或政府基金解决。另外，可采取行业联保、互保等方式分散风险，也可在国际市场上进行分保。其次，可利用现代金融业的发展，在证券、期货等金融市场上销售衍生产品以化解风险。这样可减小巨灾险对单个保险公司的影响，促进整个行业的发展。

4 结论

本文对保险索赔数据进行了多元统计分析和重尾分布的统计检验，应用R软件实现了利用剩余风险均数检验重尾分布的实证研究。

各类保险的索赔数据及其分布是保险公司研究的重要内容，本文分析了影响财产险赔付的潜在公共因子，研究结果显示财产保险索赔主要由3类潜在因素影响：工业保险、大额索赔保险和非工业特殊保险。根据索赔数据，我国的财产保险分公司呈现出依公司和地区聚类的特点，同一保险公司的不同省市分公司聚为一类，同时沿海等发达地区和内陆地区的保险公司分属不同类，此结果便于保险总公司对不同地区分公司分别管理，也便于保监会对不同保险分公司分类监管。

本文选取一系列历史数据，通过R软件编程实现了剩余风险均数理论方法的实证应用，进一步验证了工业火灾、洪灾和地震灾害造成的索赔额的分布是重尾分布，都易造成重大索赔。保险人承保此类相关财产险时要特别关注，应选取适当的重尾分布函数拟合索赔额分布，准确地由索赔确定应收保费。与需要以理论分布为参照的Q-Q图方法相比，本文方法只需相应数据即可得到检验结果，易于实现和操作，便于保险公司采纳应用。

[1]韩天雄,蒋华华.保险索赔额的分布及其应用[J].华东师范大学学报（自然科学版）,1997,(4).

[2]徐小阳,李光久.保险索赔额分布的拟合及修正[J].统计与决策,2004,(1).

[3]欧阳资生.巨灾保险索赔数据的极值风险度量 [J].统计与决策,2007,(22).

[4]Rolski,T.,Schmidli,H.,Schmidt,V.,Teugels,J.Stochastic Processes for Insurance and Finance[M].Chichester:John Wiley&Sons Ltd,1999.

[5]朱其俊,郜燕.基于多元统计分析的上市公司财务危机预警模型的研究[J].现代管理科学,2007,(5).

[6]中国保险年鉴编辑委员会.中国保险年鉴(2007)[M].北京:中国保险年鉴编辑部,2007.

[7]薛毅,陈立萍.统计建模与R软件[M].北京:清华大学出版社,2007.

[8]中国保险年鉴编辑委员会.中国保险年鉴(2003)[M].北京:中国保险年鉴编辑部,2003.