ART算法重建图像的影响因素

伍建辉,刘郁纪,李公平,汤振兴,潘小东,林俏露

(兰州大学核科学与技术学院,兰州 730000)

CT检测技术是射线扫描之后,利用不同算法求解出被测物体断层的衰减系数分布,然后把衰减系数分布转化为相应的密度分布以重现物体断层,从而达到检测物体断层内材质、几何结构和缺陷等目的。CT重建算法大致可分为变换法和代数重建法,变换法重建速度快,可以用硬件实现,但要求数据的采集必须完全且均匀,而实际应用中,由于一些客观原因的存在,投影数据的采集往往不完全或不均匀[1]。出于这种情况的考虑,ART算法应用而生,它很好地弥补了这一缺点。尽管ART算法重建速度较慢,但随着计算机技术的发展,速度逐渐成为次要问题,图像质量上升为主要问题。近年来,众多学者对不同情况下ART算法重建图像质量进行了研究[2-5]。在此基础上,笔者基于 Visual C++6.0及Matlab 7.0,仿真CT图像重建过程,对初始值的选取、先验知识如何影响重建图像质量、不同噪声下不同投影数对重建图像质量的影响等做了详细的探讨,得出了一些有益的结论,以期为实际CT检测提供一些有价值的参考。

1 ART算法

1.1 射线方程的建立

被测物体断层离散化为J=n×n个像素,对每一像素进行编号,xj表示第j个像素的像素值。定义rij=l/σ,其中l表示第i条射线通过第j个像素的长度;σ表示每一像素的长度或宽度。从而像素j对射线i的贡献为：

射线经断层后,其投影值为：

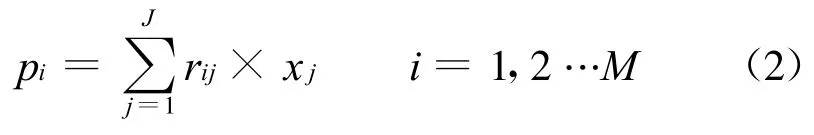
其中,rij称为加权因子。上式可写为：

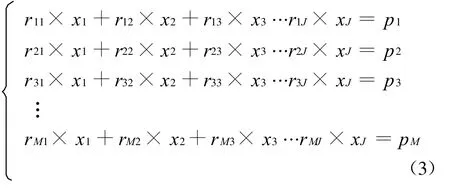
用矩阵形式表示为：

式中R,X,P分别为：

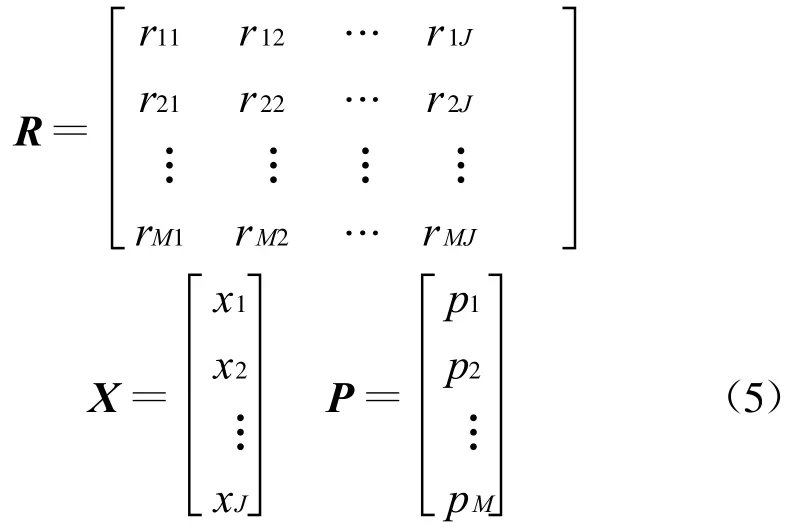
如式(3)所示,M条射线可以建立M个方程。由数学知识可知,要求出J个像素值,只有建立J个线性无关的方程才有可能精确地求出每一个像素值。在实际中,由于像素个数庞大,例如：128×128的重建区域,就需要建立128×128个方程,此外,由于噪声的存在及其它一些特殊情况,投影数的个数不一定能达到方程的个数。所以,直接求解方程在实际应用中是不可行的。ART算法通过迭代的方法很好地解决了这一问题。

1.2 ART算法分析

ART算法的基本思路为：首先,任选一初始值X0,以这一初始值为基础,进行投影运算(式(3)中每一方程代表一超平面。初始值看作J维空间内一点,然后向一超平面投影,在该超平面上得到相应的投影点)得X1,使其满足式(3)中方程1;然后以X1为基础,进行类似于上一步的运算得X2,使其满足式(3)中方程2;如此继续,直至所有射线方程计算完,最后得结果XM。然后以XM为初始值,进行下一轮运算。依此类推,直至得到满足要求的值。

ART算法中进行相应运算的公式为：

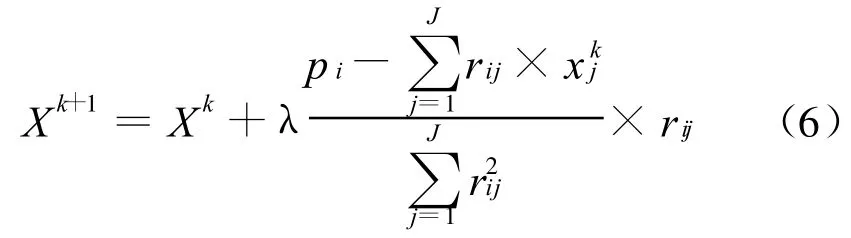
式中k为迭代序号;λ为松弛参数(其中λ应满足条件0＜λ＜2)。一般地,只有当一轮计算完毕后,才称为一次完整的迭代[2]。

J=2计算过程如图1所示。图中超平面H1,H2交于F(方程解)。X0为任选初始值,X0向超平面H1投影得X1。X1向超平面H2投影得X2。如此反复,由图可知随着投影次数增加,其投影值逐渐趋近于像素值F。此外,X′0在超平面H1上的投影值X′1较X4更接近于像素值F。所以选取合适的初始值可以在迭代次数少的情况下达到较高的精度。

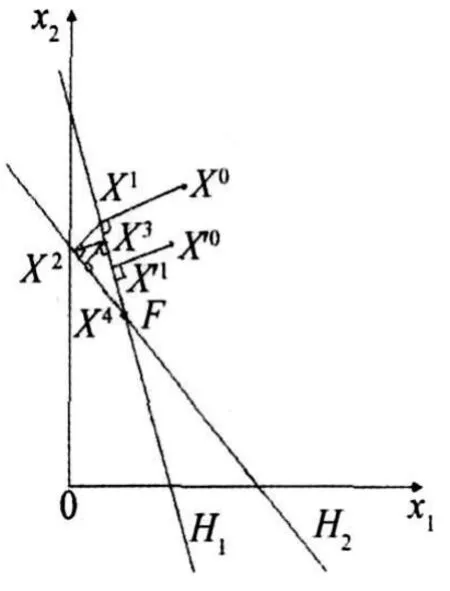
图1 二维计算过程

实际CT图像重建中,由于噪声的存在,超平面H1,H2将会有所移动,需加入松弛参数λ对投影值进行适当的调整。当0＜λ＜1时,其投影值X1位于H1超平面右上方,并随 λ增大,投影值X1逐渐趋于超平面H1;当λ=1时,其投影值X1恰好落在超平面H1上;当1＜λ＜2时,投影值X1位于超平面H1左下方,并随λ增大,投影值X1逐渐远离超平面H1。依此类推,Xk在Xk-1基础上进行相应的投影得到[2]。可见,松弛参数的选取对图像重建起着很重要的作用。

综上所述,ART算法图像重建过程中,松弛参数、初始值的选取等多方面因素对图像重建具有重要影响。

2 多因素对图像重建的影响

仿真试验中,选取128×128经典Shepp-Logan[6]头部模型为重建对象,采用每一投影角度下射线束为128的平行束扫描方式,权因子计算采用Siddon改进型[7]。为了精确评价重建图像质量,采用归一化均方距离判据d、归一化平均绝对距离判据r来定量地评价图像质量。其具体定义为：

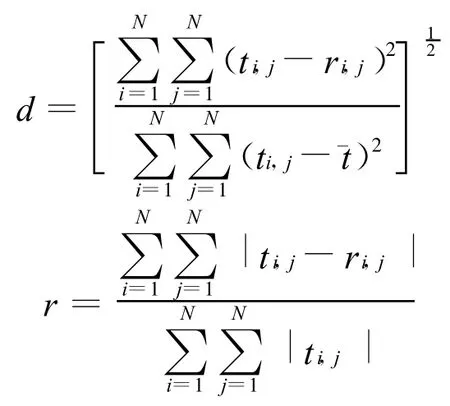
式中ti,j,ri,j分别为测试模型和重建后图像中第i行、j列的像素密度;为测试模型密度的平均值;图像的像素为N×N个。其中d较敏感地反映某几点产生较大误差的情况,而r则较敏感地反映许多点均有一些小误差的情况。判据d,r越小,表示重建图像质量越好[1]。

2.1 先验知识对重建图像质量及松弛参数选取的影响

ART算法图像重建中,一般会采用先验知识来改善图像质量。如果已经确定所有像素值都分布于某一范围内,则在重建过程中,当某像素值超出这一范围时,则强行把此像素值置为一特定值。例如,笔者所用重建模型的像素值都分布在0～1之间,当某像素值f＜0时,迭代过程中置此像素值f=0;当某像素值f＞1时,迭代过程中置此像素值f=1。图2(a)和(b)分别表示在投影数(即投影角数)为180,噪声为0,初始值F(0)={0},加入先验知识与未加入先验知识情况下重建误差分析图,其中迭代次数为1～10,松弛参数分别选取λ=0.03,0.06,0.1,0.2,0.4,0.7,1.0,1.2,1.5和1.9。

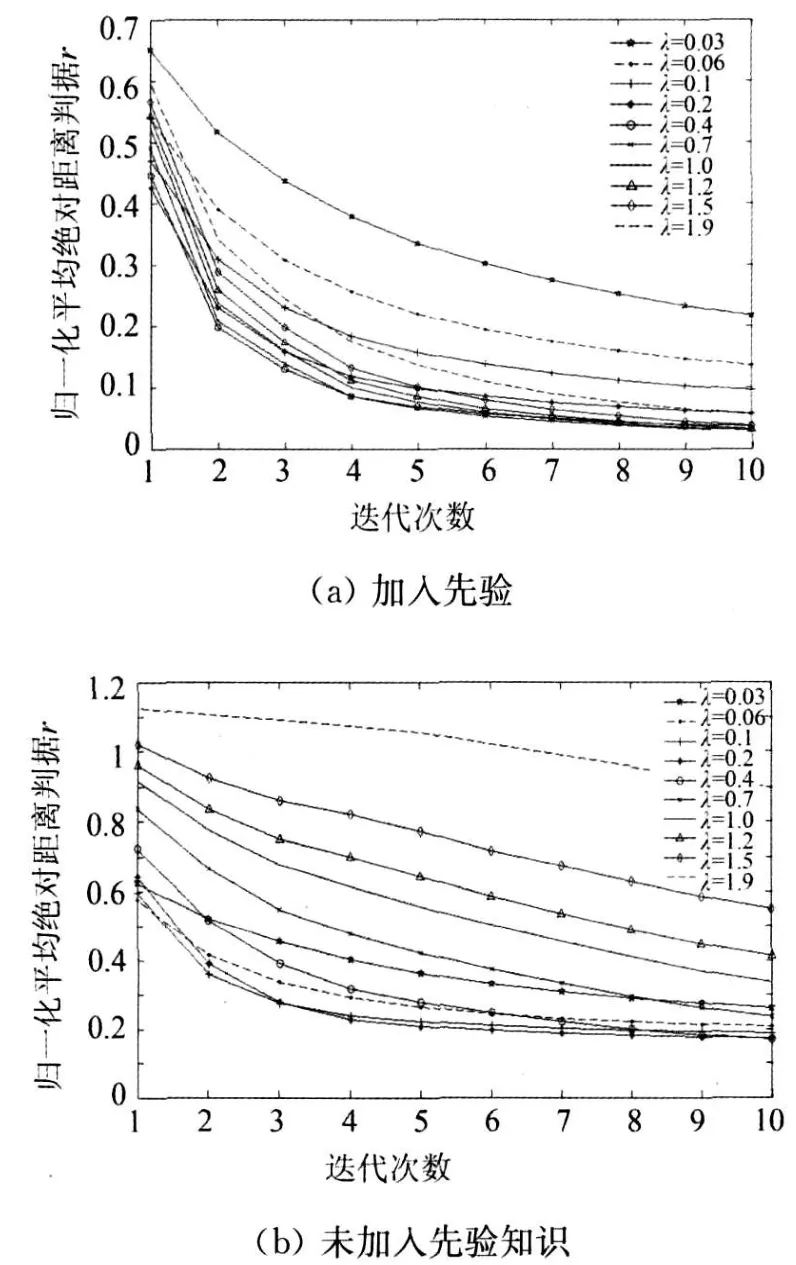
图2 先验知识对重建误差的影响

图2中当加入先验知识时,其最佳松弛参数在0.7附近,同时松弛参数较大(如松弛参数＞0.4)的重建误差随着迭代次数的增加,其下降的速度很快。未加入先验知识时,其最佳松弛参数在0.2附近,其较大松弛参数重建误差下降缓慢。表1为松弛参数等于0.2,加入先验知识与未加入先验知识情况下,r和d值的分布情况。

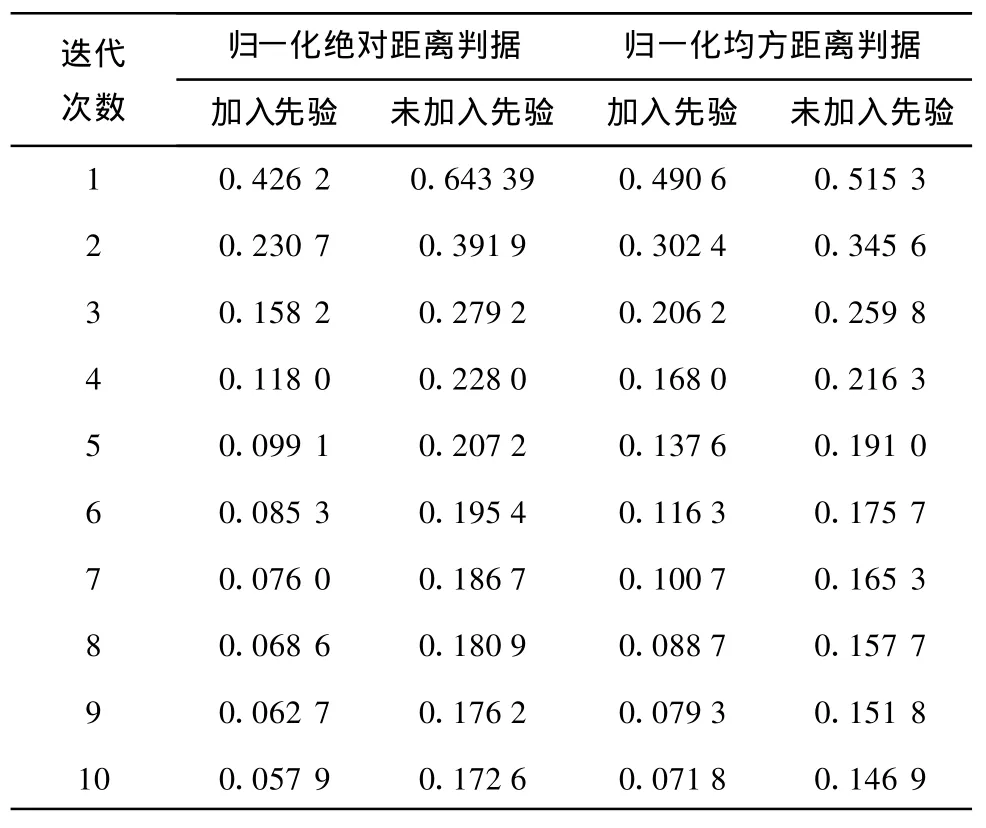
表1 先验知识对归一化绝对距离判据r及归一化均方距离判据d的影响

由表1可看出,先验知识在松弛参数为0.2的情况下对判据d,r的影响很大。表1中,未加入先验知识迭代10次的r值较加入先验知识迭代3次的r值还大;同时,未加入先验知识迭代10次的d值大于加入先验知识迭代5次的d值。

综上所述,先验知识对大松弛参数重建误差具有很好的抑制作用。当加入先验知识时,松弛参数可以适当选大一点,且经过3～5次迭代便可以取得较好的重建结果。当未加入先验知识时,其松弛参数应适当选小一点。另外,相同松弛参数下,加入先验知识,经过3～5次迭代,就可以达到未加入先验知识迭代10次时的重建效果。所以在实际检测中,应尽量加入先验知识来提高重建图像质量。

2.2 初始值对图像重建的影响

从图1可看出,选取适当的初始值可以在迭代次数少的情况下重建出精度较高的图像。图3表示投影数为180,噪声为0,松弛参数为0.4,加入先验知识,初始值不同情况下重建误差图。其中所加入的误差是以均值为0,标准差为某一值来定义(如误差为0.01,表示均值为0,标准差为0.01);选取的随机数在0～1之间服从均匀分布。

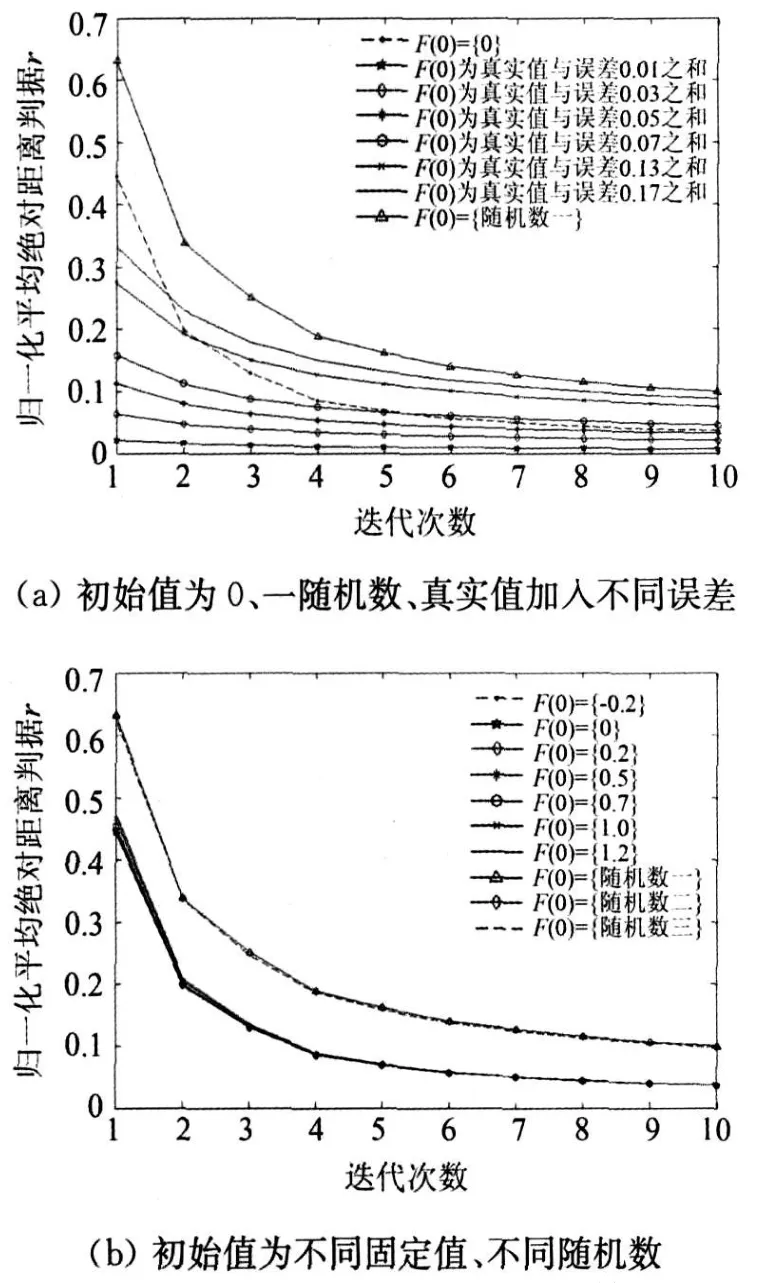
图3 不同初始值重建误差

图3(a)中初始值误差增大,其重建误差也逐渐增大。同时,初始值为0时,迭代5～6次可以达到初始值误差为0.07的重建误差。而当初始值为一随机数时,其重建误差最大,大于初始值误差为0.17的重建误差。图3(b)中,初始值取不同随机数值时,其重建图像误差大致相同。同时,初始值取不同固定值(即使超出了重建区域像素值范围)时,其重建误差也只在迭代次数少(如2～3次)时有细小差别,随迭代次数增加,其差别逐渐消失。

综上所述,选取误差较小的初始值可以在迭代次数少的情况下重建出误差较小的图像,如当初始值误差＜0.07时,迭代2～3次便可得出质量较高的图像。在完全不知真实值情况,但可以确定像素值分布范围时,初始值取一固定值为较佳选择。

2.3 不同投影数在不同噪声下对松弛参数选取及重建图像的影响

式(3)中,如果线性无关方程个数越多,则M维空间中能确定精确解的范围将会越小,由此可推知投影数对图像重建具有重要的影响。此外,在实际CT检测中,不可避免地存在噪声,这对图像重建的影响也是不可忽视的。在仿真投影数据中,分别加入均值为0,标准差为0.1,0.2,0.4的高斯白噪声;采用投影数为180,128,90,36;为了考虑实际情况,选取松弛参数为0.01,0.03,0.06,0.1,0.2,0.4,0.8和1.0。重建误差如图4,5和6所示。

比较图4,5和6可看出,相同噪声下,投影数增大,其最佳松弛参数逐渐减小。相同投影数下,噪声增大,其最佳松弛参数逐渐减小。此外,投影数、噪声都较大时,一些松弛参数重建误差将发散,如图6(a)和(b)中,松弛参数＞0.2的重建误差不收敛;投影数较小时,其松弛参数选取对噪声的敏感度也较小,如投影数为36时,在噪声从0变为0.4的情况下,其较佳松弛参数的选取几乎保持不变。同时,从各图中可看出,当投影数减小及噪声增加时,都会增加重建图像的误差。

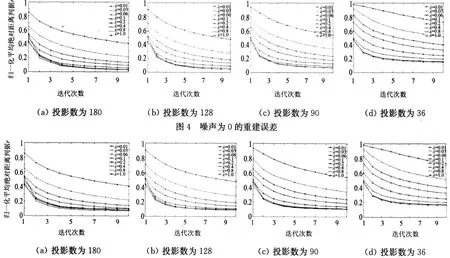
图5 噪声为0.2的重建误差

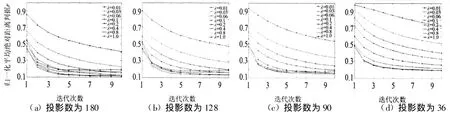
图6 噪声为0.4的重建误差

上述仿真过程为加先验知识时的情况。但未加先验知识时,其噪声、投影数对松弛参数选取及图像重建的影响具有相同的趋势,只是其最佳松弛参数较加先验知识时要小得多,如投影数为180时,其最佳松弛参数随噪声的变化,其值在0.2～0.06之间变化,限于篇幅,此不赘述。

2.4 缺角度对图像重建的影响

实际CT检测在一些特殊情况下,可能不能扫描某些角度,此时,可以用ART算法来重建图像。图7描述了松弛参数为0.4、迭代次数为8、在均匀投影数为180的基础上缺失4,8,12,…,60°的重建误差。图8为松弛参数等于0.4、迭代 8次、在均匀投影数为80,100,120,140,160,185,210,230,250,270和290基础上缺失20°与40°的误差分析图。图9为均匀投影数为80,185和290基础上缺20°的重建图及第80行重建像素值分析图(注：某均匀投影数基础上缺角度是指某投影数在180°范围内均匀分布后缺失角度数)。

由图7可看出,其重建误差与所缺度数几乎成线性关系。在图 8中,不同投影数下缺 20°或 40°,都可以通过均匀增加投影数减小其重建误差。从图9可以看出,通过均匀增加投影数,可以很好地抑制重建过程中产生的误差。综上所述,实际扫描过程中,当缺失一定的度数时,可以通过均匀增加投影数来减小其重建误差。

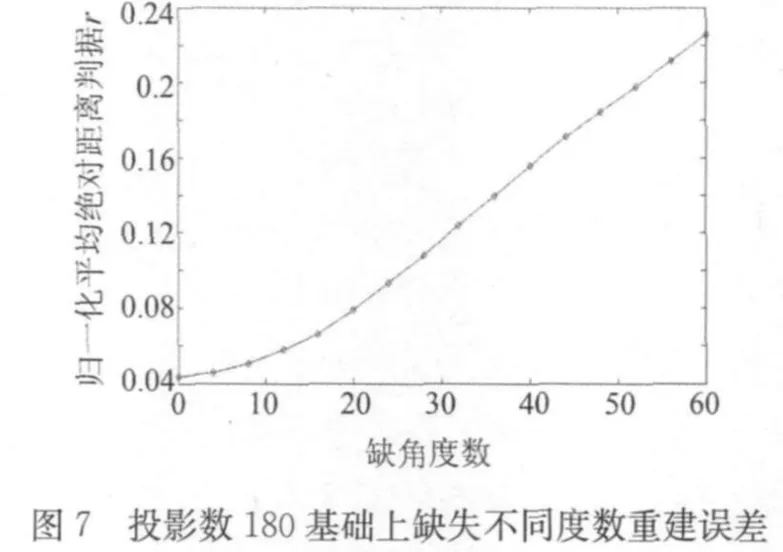
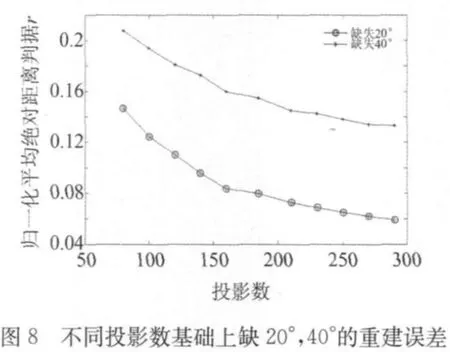
图 9 不同投影数基础上缺20°的重建分析图

3 结论

初始值、先验知识、投影数和噪声等对图像重建具有很大影响。在实际CT检测中,如能预先获得一些被测物像素值信息(如要检测某已知产品一些细小裂缝或杂质,则可以把接近于被测物的像素值作为初始值)时,则迭代2～3次便可以达到较高的分辨率,这样就可以缩短检测时间。此外,要尽可能利用被测物先验知识,这样可以在很大程度上改善重建图像质量,同时在加入先验知识后,应适当地提高松弛参数值。一般地,当加入先验知识时,在噪声较大、投影数较多的情况下,应选择较小的松弛参数(如0.06～0.1之间);当噪声较小投影数较少时,松弛参数可以适当地取大一点(如0.4～0.7之间)。ART算法作为一种有效的迭代算法,可以在缺失角度情况下重建出较好的图像,当缺失一定角度时,可以通过均匀增加投影数的方式来改善重建图像质量。另外,通过进一步研究发现,在一定投影数下,随着缺失度数的增加,其最佳松弛参数逐渐增大。

[1]庄天戈.CT原理与算法[M].上海：上海交通大学出版社,1992.

[2]张顺利,张定华,熬波,等.ART算法高质量重建研究[J].核电子学与探测技术,2007,27(4)：719-720.

[3]张顺利,张定华,王成,等.投影数对ART算法重建质量的影响[J].无损检测,2008,30(12)：889-891.

[4]冷帅,张丽,陈志强,等.迭代算法用于投影数据不完备时重建断层图像的研究[J].核电子学与探测技术,2003,23(3)：216-219.

[5]高欣,夏顺仁,汪元美,等.一种不完全投影图像重建的快速迭代算法[J].浙江大学学报(工学版),2004,38(9)：1108-1111.

[6]Shepp L,Logan B P.The Fourier reconstruction of a head section[J].IEEE Trans Nucl SCI,1974(NS-21)：21-43.

[7]张顺利,张定华,李山,等.ART算法快速图像重建研究[J].计算机工程与应用,2006,42(24)：2-3.