有资本转移的二元经济内生增长模型

姚洪兴,王佳音

（江苏大学 理学院，江苏 镇江 212013）

一般认为，中国经济的高速增长发生在传统经济向现代经济的转变过程之中，是伴随着二元经济结构转换的经济增长[2][3]。而新古典增长理论是一元经济结构的增长理论，没有分析到资本投入对二元结构经济增长的作用，同时也忽略了劳动力从农业部门向产业部门转移对经济增长的贡献[1][4]。本文拟在借鉴内生增长理论思想的基础上，将资本转移内生化，建立一个二元经济增长模型，并通过动态最优化的方法，对农业部门和产业部门的均衡发展进行模型分析，解释资本转移与系统均衡的关系。

1 模型的建立

1.1 理论假设

在一个封闭的二元经济系统中存在着两个部门，农业部门与产业部门，假设人口增长忽略不计，总人口设定为1，全部人口为全部劳动力。劳动力的工资收入全部用于消费，以最大化一生效用。在经济发展的初级阶段，劳动力主要集中在农业部门，因此产业部门没有足够的劳动力以发展经济。同时，农业部门因缺乏经济发展所必须的资本而使劳动生产率低下。从而导致整个系统的经济停滞不前。经济发展处于一个低层次稳定均衡。随着经济的深入发展，要求产业部门有一定量的资本转移到农业部门，假设资本转移增长率为θ。随着资本的转移，农业部门有相应的劳动力向产业部门流入，并且劳动力转移速度受资本转移的影响，其转移速度同样是θ，很显然，0<θ<1，这样才能确保两部门有经济发展所必需的有效劳动数量。

1.2 农业部门

农业部门用资本Kz、有效劳动数量Lz进行生产，规模收益不变，假设其生产函数满足柯布—道格拉斯总量生产函数：

其中，农业部门资本的增量为：

有效劳动的数量为：

u表示在农业部门就业的劳动力比例，因而v=(1-u)就构成在产业部门就业的劳动力比例。对Lz求偏导，由（1）～（3）式可得农业部门劳动力的工资率：

从上式可以看出，工资率与有效劳动数量成反比，原因在于边际劳动生产率的递减。另外，产业部门的资本投入是农业部门技术进步的前提，因此随着θ的增大，农业部门的工资率Wz增大。

1.3 产业部门

产业部门用资本Ky、有效劳动数量Ly进行生产，同时产业部门将吸收来的劳动力转化为投资回报投入再生产，假设投资回报为R,其生产函数同样满足柯布—道格拉斯函数，且规模报酬不变，则有：

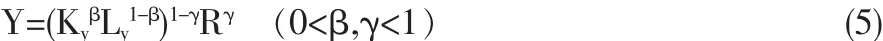
根据上面的假设，产业部门雇佣v=(1-u)比例的劳动力，同时又从农业部门吸收θu数量的劳动力，因此有效劳动数量为：

由于投资回报R决定于吸收的有效劳动数量Lx=θu，假设单个劳动力的投资回报为W，则产业部门的资本增量可以表示为：

θK表示产业部门转移到农业部门的资本量。

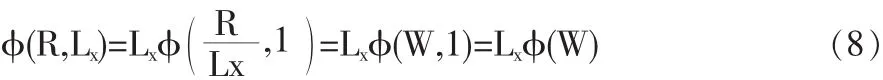
式（8）代表的经济含义是：由于投资回报并不是全部转换为投资，因此假设吸收的有效劳动数量带来的回报只有φ部分转化为投资，φ表示中介系数，且0≤φ≤1。显然，φ是关于有效劳动力的工资比例W的函数，且φ由uθ决定，有关系式

由上，（7）式可以表示为：

在政府的宏观调控下，产业部门有资本转移到农业部门，以促进农业部门的技术进步。但同时产业部门也要保证本部门在经济发展中的资本投入，因此投资回报要不低于资本转移量，这样产业部门才会有资本转出。（9）式从整体上描述了资本转移的可能性以及资本转移实现的条件，即

由（6）式和（9）式可得产业部门劳动力的工资率：

1.4 消费者行为

在上述经济系统中，消费者的工资收入用于消费，假设未来不存在不确定性，消费者的效用函数具有不变跨期替代弹性，其函数形式为：ρ为时间偏好率，ρ＞0。u(c)为即期效用函数，且 u(c)=为边际效用的弹性，且σ＞0。

消费者预算约束为消费者消费的现值不能超出其工资收入：

消费者选择消费路径以最大化一生效用，则有如下最优化问题：

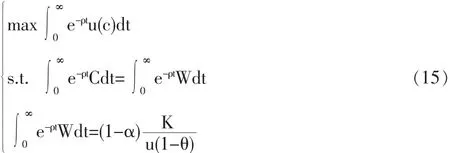
2 稳定性分析

2.1 均衡

证明：由于劳动力在农业部门和产业部门自由流动，因此均衡时两部门的实际工资率应该是相等的，即 （4）式与（11）式相等，即有：

证明：（15）式说明了消费者一生的工资收入，由于劳动力在部门间完全流动，平衡时农业部门和产业部门之间的实际工资率是相同的。根据动态最优化方法，构造Hamilton方程：

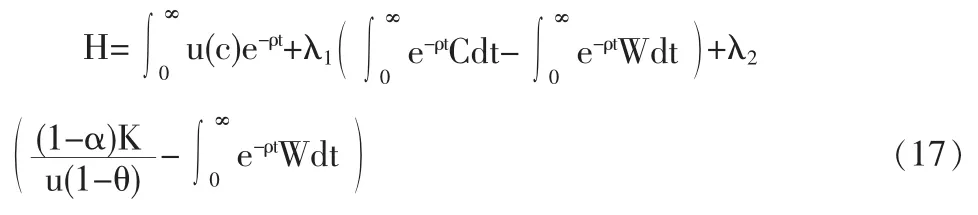
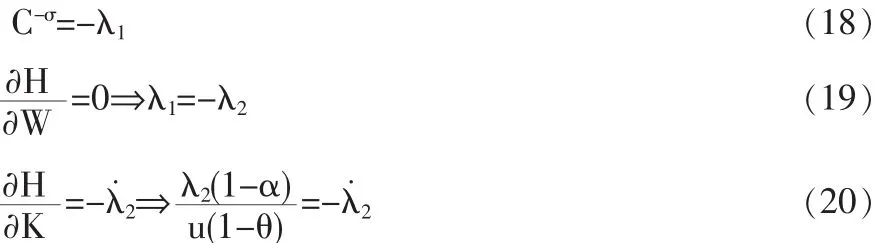
对（18）式去对数求导后可得：

由（19）～（21）式整理可得欧拉方程：

欧拉方程（22）衡量了消费的增长速度。从方程可以看出，随着θ的增大对农业部门的经济增长率有两方面的影响，首先θ的增大意味着资本转入量的增多，从而通过促进技术进步使经济增长率提高；另外，θ的增大说明农业部门多余劳动力的转出，从而使本部门达到充分就业，人均消费水平上升。但考虑到就业量和资本的关系，θ不能无限量的增大，当θ过大，使得农业部门就业量下降时就会导致资本边际生产率下降，从而影响到人均消费。

由于φ表示产业部门转移资本的回报转化为本部门投资的比例，因此 I=K˙=φLx-θK。 显然：

上述方程衡量了资本的积累速度。

2.2 模型分析

gk与gc随θ的变化可用图1来表示。

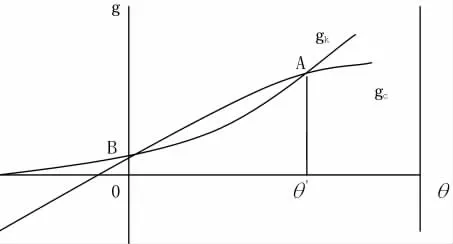
图1

图1 中的θ'表示农业部门与产业部门实际工作率相等时θ的值。随着θ的增加，产业部门就业量增加，在不考虑其他因素的情况下，由于边际替代率递减的规律，随着劳动力投入数量的增加，产业部门劳动生产率单调递减，从而引起劳动工资率的增量单调递减，最终表现为消费的增长速度增量单调递减；同时农业部门的工资率也会随着本部门劳动力的减少而增加，具体表现为图1中的gc曲线。当θ增加到θ'点时，即当整个系统达到均衡状态时，消费的增长速度将不再增加。

由于θ描述资本转移增长率，因此θ的增加意味着农业部门资本积累速度的增加，如图1中gk曲线所描述。讨论产业部门，由 Lxφ(W)≥θK 得 uφ≥K,因此K˙'=uφ-K≥0，即产业部门投资回报引起的规模经济使得资本积累速度单调递增。

在长期内，当经济处于均衡时，有也就是当 g曲k线和gc曲线相交时，经济处于长期均衡状态。由图1可以看出，gk和gc曲线的两个交点A、B为长期均衡点。其中B点的均衡是不稳定的。在B点时，θ=0，没有资本及劳动力的转移，经济增长处于贫困陷阱中，是一个低层次的稳定均衡，这时劳动力集中在农业部门。由于劳动力的自由流动及政府的宏观调控，必然有劳动力的转移，从而打破平衡状态。在BA阶段，开始传统经济向现代经济的转变。由于资本的转移，产业部门带领农业部门脱离贫困陷阱，此时劳动力也得到充分就业，整个系统的劳动生产率提高，资本转移起到了促进经济增长的作用，并在A点均衡，经济增长进入良性循环。

3 结论

本文通过吸收内生增长理论的思想，将资本转移引入模型中，分析了有资本转移情况下整个二元经济系统的经济增长及均衡状态。通过对模型的分析，本文认为，产业部门与农业部门间的资本转移，可以在一定程度上帮助整个经济系统摆脱贫困陷阱，并最终达到一个高水平均衡。

[1]左大培，杨春学.经济增长理论模型的内生化历程[M].北京：中国经济出版社，2007.

[2]陈宗胜，黎德福.内生农业技术进步的二元经济增长模型[J].经济研究，2004，（11）.

[3]郭涛，宋德勇.农村劳动力转移的二元经济内生增长模型[J].南方经济，2006，（8）.

[4]龚六堂.经济增长理论[M].武汉：武汉大学出版社，2000.

[5]Sajid Anwar.Sector Specific Foreign Investment,Labour Inflow,Economies of Scale and Welfare[J].Economic Modelling,2009，（26）.

[6]Das,S.P.Foreign Direct Investment and the Relative Wage in a Developing Economy[J].Journal of Development Economics,2002，67（1）.

[7]彭文平.金融发展阶段：一个包含金融部门的内生增长模型[J].华南师范大学学报,2007，（3）.

[8]刘群峰，胡适耕.制度内生的随机经济增长模型[J].东莞理工学院学报，2005，12（1）.

[9]Sajid Anwar.Variable Labour Supply,Specialization-Based Exter⁃nal Economies,and Capital Inflow[J].International Review of Eco⁃momics and Finance,2005，14.

[10]Sajid Anwar.Factor Mobility,Wage Inequality and Welfare[J].In⁃ternational Review of Ecomomics and Finance,2008，17.

[11]姚洪兴，吴晖琴.资源约束下的一类内生经济增长模型[J].佳木斯大学学报，2007，25（1）.

[12]姚洪兴，吴承尧.一类金融古诺混沌模型的分析与控制[J].系统工程理论与实践，2007，（5）.

[13]Lucas，Robert.On the Mechanics of Economic Development[J].Journal of Monetary Economics,1988，22.

[14]徐峰,盛昭瀚,姚洪兴.延迟决策对一类双寡头广告博弈模型的影响分析[J].管理科学学报，2007，10（5）.