葛洲坝护坦新旧混凝土粘结面水压力分布规律研究

杜利民

(中国长江电力股份有限公司,湖北 宜昌 443002)

葛洲坝护坦新旧混凝土粘结面水压力分布规律研究

杜利民

(中国长江电力股份有限公司,湖北 宜昌 443002)

葛洲坝护坦底板修补材料极易被高速水流冲蚀破坏,影响大坝安全稳定运行。根据护坦底板新浇筑材料与旧混凝土粘结面缝隙脉动水压力的分布规律,建立了接触面缝隙脉动压力传播的两个阶段即渗流和瞬变流阶段的数学模型,并对实际工况进行了模拟计算。结果表明,闸室底板粘结面水压力在渗流条件下,沿程各点脉动水压力频率与尾部的原生脉动压力频率保持一致,沿程各点脉动水压力振幅与x/L成正比;在瞬变流条件下,粘结面中部点的脉动水压力由与尾部点原生脉动压力相似的低频脉动和间杂在整个过程中的高频脉动组成;沿程阻力系数对缝隙水压力的影响主要体现在对高频脉动的削弱;渗流条件下其振幅沿程增大,在瞬变流条件下,各点脉动压力振幅沿程分布变化不明显。修补材料粘结面的疲劳破坏属于应力疲劳,修补材料整体揭底冲毁为其中的破坏形式之一,整体揭底破坏与新旧材料之间粘结面疲劳损伤关系密切。

护坦底板;粘结面;渗流;瞬变流;特征线法;脉动压力

葛洲坝泄水闸闸室底板由于开启频繁,运行时间长,使得闸室底板受到长期的冲蚀,破坏严重。根据检修规程,每间隔一定时期即对底板进行检查修补。底板在经过修补后,变得凹凸不平,水力条件变差,这又进一步加剧了冲蚀破坏程度。修补材料的破坏形式一般可分为三种。第一种为空化,空蚀;第二种为高速含沙水流的磨蚀作用;第三种为整体揭底破坏。整体揭底破坏与修补材料粘结面在脉动压力作用下损伤疲劳有关。要解决这种疲劳破坏问题,必须先了解粘结面缝隙脉动水压力分布规律,以往各种文献中都集中于对岩体缝隙中的脉动压力传播机理进行探讨。Fiorotto和Rinaldo[1～3]提出用瞬变流模型探讨缝隙内脉动压力波的传播特征;张建明,杨永全等[4,5]研究认为缝隙磨阻对脉动压力影响很大,特别是高频脉动压力;李爱华,刘沛清等[6～9]利用瞬变流模型探讨了岩缝中脉动压力传播机理。而本文研究的实际工程情况则为新浇注混凝土与旧混凝土粘结面缝隙的水压力分布规律,其特点为缝隙直径小,缝隙内水体运动规律随着运行时间的增长而发生变化,以时间段划分大致可分为渗流阶段和瞬变流阶段。在这种小直径下,缝隙脉动压力分布呈现新的特点。

1 闸室修补后底板情况

修补后闸室底板如图1所示。封边材料为环氧树脂,封堵缝隙,使修补粘结面与外界隔绝。修补材料与闸底粘结面由于新旧混凝土性能差异,温度,以及施工工艺等因素影响存在缝隙。破坏,新旧材料之间缝隙与外部连通,从而使得修补粘结面缝隙受到B处紊流脉动压力影响。修补材料粘结面脉动压力发展经过两个阶段。

图1 修补后闸室底板示意图

第一阶段,初期由于缝隙较小,缝隙表面粗糙,阻塞严重,此时缝隙水流状态为渗流,B处脉动压力以渗流形式传入缝隙。

第二阶段,随时间推移,在水体反复作用下缝隙开度增加,粗糙度减小,渗透性增加,水体流动不符合渗流特征,缝隙内水体在受B处脉动压力影响,而成为瞬变流。

最后,由于材料接触面不断受到脉动压力影响,使得接触面粘结材料发生疲劳,导致发生修补材料整体揭底破坏。

本文将集中研究第一、第二阶段时,缝隙水压力的分布特征。

2 接触面缝隙脉动压力传播模型

如图1所示,B点的脉动压力可以表示为:

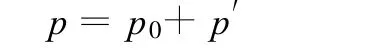
式中:p0为实测的时均值,实际运用中,可取静水压力,即p0=γH0,H0为自由水面至护坦底板高度;p′为随着时间变化的压力分布。因实际运行时对B点脉动压力无法进行实测,采用简化处理,假设p′=Asin(2πft)。

第一阶段,缝隙水体运动为渗流,服从 Darcy定理,此时脉动压力以渗流速度传播,有控制方程:

式中:γ为水体容重;k为缝隙渗透系数;p为缝隙内水压力。

将式(2)代入式(1)可得:

将式(4)代入式(3),可得:

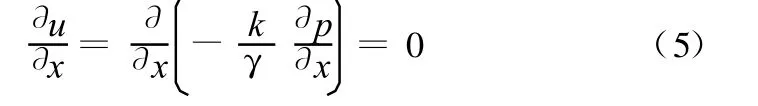
对式(5)进行积分,可得:

式中:C1,C2为积分常数。

在A点处,缝隙内水流通过环氧封边材料与平整护坦底板以及修补材料之间的缝隙,同上游水流连通,可认为当x=0,p=PA=p0=γH0。在B点处,即当x=L,p=PB=γH0+Asin(2πft)。

代入边界条件解式(6)得:

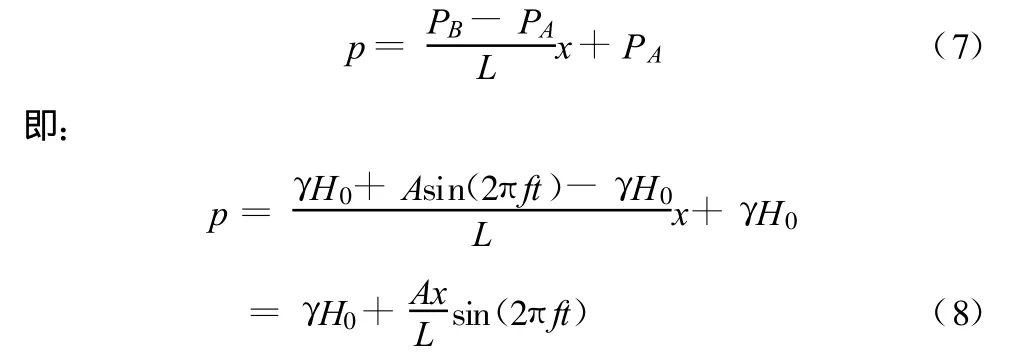
两边同时除以 γ,可得:

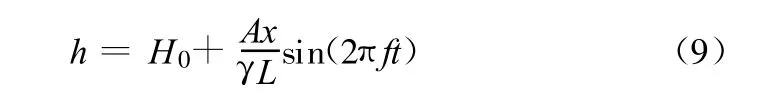
式(8)揭示了脉动压力在渗流模型下沿程分布的情况。

第二阶段,随着缝隙长期不断淘洗,使得缝隙增大,缝隙内水体流动呈现瞬变流特征。建立了一维瞬变流模型,如下:

式中:g为重力加速度;C为压力波传播速度;f为阻力系数;D为缝隙直径。

式(10),(11)为一组拟线形双曲型偏微分方程,难以直接求出解析解。可利用特征线法计算其近似解。

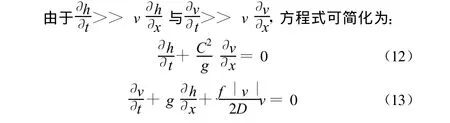
利用特征线法处理式(12),(13),可得:

对其积分并采用一阶近似积分代替,可得:

简化式(14),(15),可得:

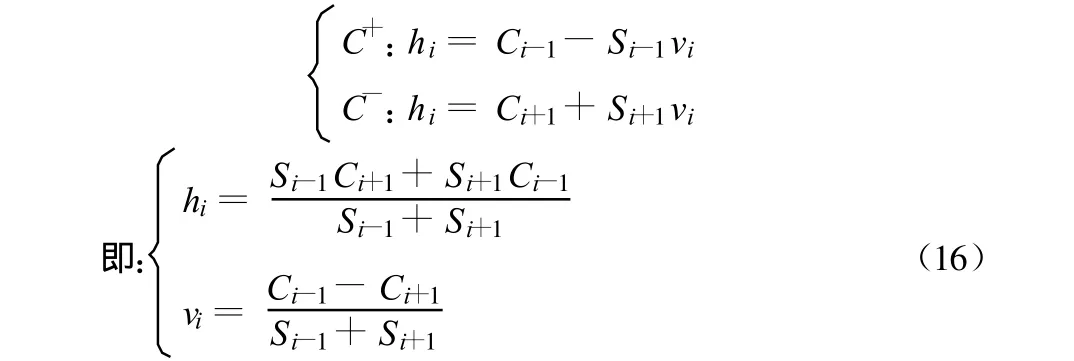
利用式(16),加上粘结面初始条件与边界条件便可利用计算机解出缝隙脉动水压力的分布特征。

3 实际工况模拟计算

3.1 模拟工况说明

3.2 第一阶段计算结果

在第一阶段(渗流阶段),利用公式(9),绘出x/L=0,x/L=1/4,x/L=1/2,x/L=3/4,x/L=1点水头分布规律,如图2所示。

3.3 第二阶段计算结果

第二阶段下利用公式(16)计算缝隙脉动水压力分布情况。由于水流是从渗流状态转变为瞬变流状态,而渗流状态时流速很小,可认为初始流速为0,同时选取渗流时平均水头3 m为初始水头,取波速C=1 000 m/s。

选取空间步长 Δx=0.1,则时间步长 为 Δt= Δx/C=0.1/1000=0.0001利用该初始条件计算修补材料中各点水压力在不同阻力系数下的分布情况,计算结果如图3～图6所示。

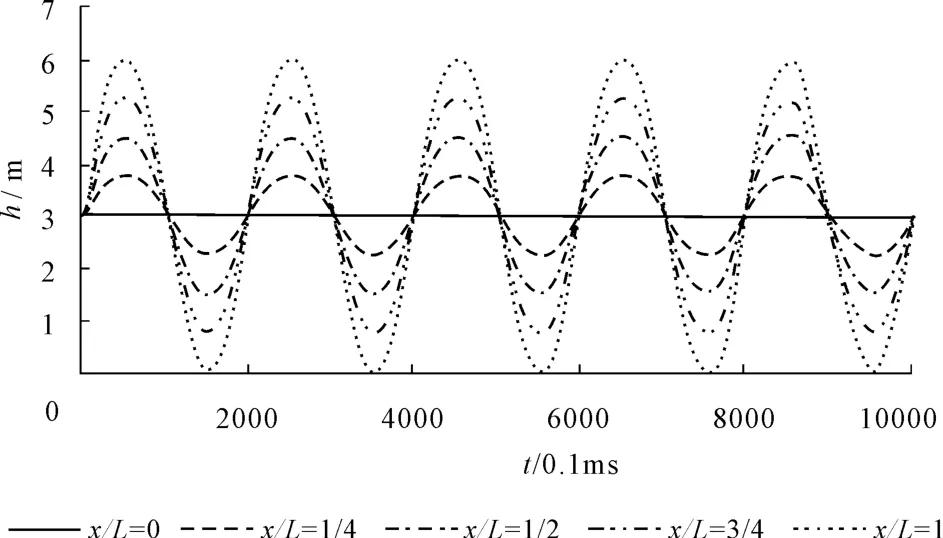
图2 第一阶段水头分布规律图

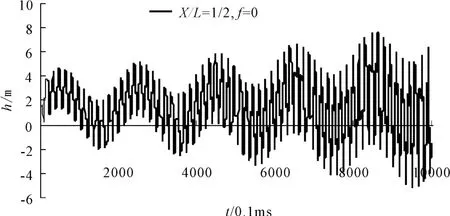
图3 第二阶段各点水压力分布情况(f=0)

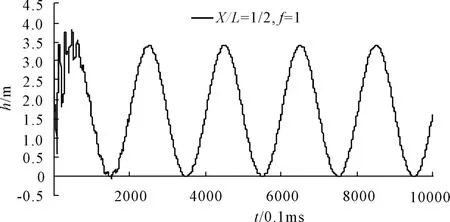
图4 第二阶段各点水压力分布情况(f=1)

3.4 图形比较分析

对以上图形分析可得出以下几点:

(1)从图2中可以看出,闸室底板粘结面水压力在渗流模型条件下,其分布规律为:沿程各点脉动水压力其频率不受其它因素影响,与B点的原生脉动压力频率保持一致;沿程各点脉动水压力振幅随着越往下游走越大,其增加幅度与x/L成正比。

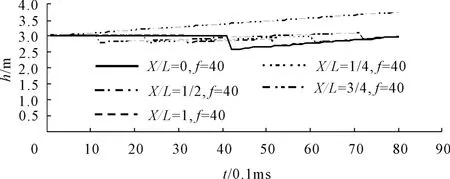
图5 第二阶段各点水压力分布情况(f=40,局部)

图6 第二阶段各点水压力分布情况(f=40,整体)

(2)从图3中可知,随着运行时间增加,闸室底板粘结面水压力在瞬变流条件下,当沿程阻力系数为0时,修补材料粘结面x/L=1/2点的脉动水压力分布规律为:其脉动水压力分为两部份,一部分是与B点原生脉动压力相似的低频脉动,其频率与B点一致,而另一部分则为间杂在整个过程中的高频脉动,其频率约为低频脉动的14倍;脉动压力的振幅是随着时间的增加而增大,从理论上说可随时间增加得到无限大。由于粘结面缝隙是小缝隙,在实际运行中,阻力系数是肯定存在,这种沿程阻力系数为0在实际运行情况中不可能出现。

(3)通过对图4与图3比较,可发现在沿程阻力系数对缝隙水压力的影响主要体现在对高频脉动的削弱,高频脉动对沿程阻力系数很敏感(图4的沿程阻力系数仅为1)。从图4中可以看出在经过一个低频脉动周期后,高频脉动已经被削弱殆尽,随后缝隙水压力进入与渗流模型(图2中x/L=1/2曲线)类似的正弦波分布状态,但均值、振幅与渗流条件下不同。

(4)从图5与图6中可看出,在选取缝隙沿程阻力系数较大时(f=40,此情况更加贴近实际运行状况),缝隙脉动水压力分布在初始阶段(约为 0～8 ms内)会有跳动,但随后由于沿程各点脉动压力分布在频率和振幅上都趋于一致。将图6与渗流条件下(图2)相比较,其频率一致。在瞬变流条件下,各点脉动压力振幅沿程分布不发生明显变化,各个点脉动压力其分布情况一致,而渗流条件下其振幅沿程增大。

4 结 论

修补材料粘结面的疲劳破坏应属于应力疲劳。在应力疲劳分析中,荷载的频率及振幅确定甚为关键。通过本文的研究可以得出以下两点结论:

(1)在对修补材料粘结面疲劳分析时,其荷载的频率可选取与B点原生脉动压力相同的频率作为粘结面各点的脉动频率,频率的选取与缝隙内的水体流动状态无关。这点与文献[6～9]研究成果不同,主要原因在于文献主要研究岩石缝隙中脉动水压力传播机理,而本文新旧混凝土粘结面缝隙直径数量级与文献所处情况不同以及本文研究了缝隙发展过程对水体影响所导致。由于缝隙直径过小(本文为1 mm)以及沿程阻力系数存在,使得缝隙内水体运动无论在渗流状态还是瞬变流状态,其脉动频率与B点原生脉动频率相比,不产生变化。

(2)对粘结面各点脉动压力振幅则需要分别考虑水体渗透状态与瞬变流状态两种情况,在渗流条件下粘结面各点脉动压力振幅沿程增加,在瞬变流条件下各点沿程不变。

[1]Fiorotto,V,Rinaldo A.Fluctuating uplift and lining design in spillway stilling basins[J].Journal of Hydraulic Engineering,ASCE,1992,118(4):578-596.

[2]Fiorotto V,Rinaldo A.Turbulent pressure fluctuations under hydraulic jumps[J].Journal of Hydraulic Engineering,IAHR1992,30(4):35-45.

[3]Beliin A,Fiorotto V.Direct dynamic force measurement on slabs in spillway stilling basins[J].Journal of Hydraulic Engineering,ASCE,1995,121(10):645-656.

[4]张建民,杨永全,戴光清,等.水垫塘底板缝隙中脉动水压力传播规律特性[J].四川大学学报,2000,32(3):5-8.

[5]杨永全,戴光清,等.高拱坝泄洪水垫塘衬砌稳定性研究[J].云南水利发电,2000,16(2):22-25.

[6]李爱华,刘沛清.脉动压力在板块缝隙中传播衰变机理研究[J].水利水电技术,2006,37(9):33-37.

[7]李爱华,刘沛清.岩石河床在冲击水流脉动压力作用下的解体破坏机理[J].水利学报,2007,38(11):1324-1328.

[8]李爱华,刘沛清.脉动压力在消力池底板传播的瞬变流模型和渗流模型统一性探讨[J].水利学报,2005,36(10):1236-1240.

[9]刘沛清,邓学蓥.多级板块缝隙中脉动压力传播过程的数值研究[J].力学学报,1998,30(6):662-670.

Research on Hydraulic Fluctuating Pressure Distribution Between New and Old Concrete Binding Surfaces on Gezhouba Dam's Apron

DU Li-min
(China Yangtze River Electric Power Co.,Ltd.,Yichang,Hubei443002,China)

The repair material on Gezhouba dam's apron slab is easy to be damaged by the high speed flow from the spillway,which would impact on the normal operation of the dam.Here,based on the hydraulic fluctuating pressure distribution between the new and old materials,the mathematical models in two stages for pressure transmission are set up,such as the seepage flow stage and the transient flow stage,at the same time,themodelling and computation are made for the actual conditions.The results show that the fatigue damage between the binding surfaces belongs to the stress fatigue,and the monolithicwashing damage is in close relationship with the fatigue damage between the binding surfaces.

apron slab;binding surface;seepage;transient flow;characteristics method;fluctuating pressure

TV431

A

1672—1144(2010)02—0147—04

2009-12-25

2010-01-04

杜利民(1986—),男(汉族),四川人,助理工程师,主要从事水工建筑物维护管理。