碳纤维加固钢筋混凝土梁受弯性能非线性有限元分析

于 龙

(1.兰州理工大学土木工程学院,甘肃兰州 730050;2.郑州市管城建设综合开发总公司,河南 郑州 450053)

碳纤维加固钢筋混凝土梁受弯性能非线性有限元分析

于 龙1,2

(1.兰州理工大学土木工程学院,甘肃兰州 730050;2.郑州市管城建设综合开发总公司,河南 郑州 450053)

研究混凝土、受拉钢筋和CFRP在开裂、屈服、破坏各阶段的工作状态和受力特点,对认识CFRP加固机理和性能有着重要意义。应用ANSYS建立碳纤维加固钢筋混凝土梁有限元模型,利用单元生死技术模拟CFRP的不同工作状态,对试件梁开裂、屈服、破坏全过程进行非线性有限元分析。分析表明:在钢筋屈服后,CFRP加固钢筋混凝土梁在后期抗弯刚度、延性和极限承载能力方面均有增强;在结构承受较大初始荷载情况下,二次受力问题对加固梁的抗弯刚度、极限承载能力、延性存在一定影响;由于CFRP是在钢筋进入屈服阶段,应力停止增长后才发挥巨大作用,二次受力时的加固也能取得较好效果;分析结果与实测数据吻合。

碳纤维(CFRP);钢筋混凝土(RC)梁;非线性有限元分析;二次受力;单元生死

0 引 言

碳纤维(CFRP)复合材料加固钢筋混凝土(RC)是在近年来国内外广泛采用的一种混凝土外部补强新技术。由于CFRP理论上发挥自身受拉高强性能需要足够的应变,混凝土作为一种脆性材料其本身应变范围又有限,因此CFRP加固混凝土特别是考虑二次受力时的效果及其极限承载能力一直是该领域关注和讨论的热点。对CFRP加固机理、性能深入认识必须以充分了解各材料在不同阶段的工作状态为前提。本文利用ANSYS建立有限元模型,研究了混凝土、受拉钢筋和CFRP在开裂、屈服、破坏各阶段的工作状态和受力特点,利用单元生死技术研究了实际工程应用中存在的CFRP“二次受力”问题。

1 有限元分析

1.1 分析方案

试验梁为简支梁,截面尺寸及配筋情况[1]如图1所示,材料性能如表1～表3所示[1～3]。分 3种情况:①梁底不粘贴CFRP(对比梁B1);②梁底初始满贴一层CFRP(不考虑二次受力梁B2);③受荷100 kN后梁底满贴一层CFRP(考虑二次受力梁B3)。通过钢分配梁分别在距离梁两端1 050 mm位置各施加竖向集中荷载P/2,采用逐级加载方式,直至构件破坏。试验梁配置了较多抗剪箍筋以避免构件在加固区正截面适筋梁破坏前出现斜截面破坏[1]。

1.2 单元选取

对于钢筋混凝土这种典型的复合材料结构,采用分离式模型,选用:专门为混凝土、岩石材料开发的八节点、六面体单元Solid65模拟混凝土;3D空间杆单元Link8模拟钢筋;平面内具有膜强度,平面外没有抗弯刚度的膜单元Shell41模拟CFRP[4]。考虑混凝土开裂后的应力松弛,膜单元Shell41根据CFRP受力特性设置为只能受拉。

图1 梁截面尺寸及配筋示意图

表1 混凝土力学性能

表2 钢筋力学性能

表3 CFRP力学性能

1.3 本构关系

1.3.1 混凝土本构关系

采用美国学者Hognested提出的无约束混凝土应力应变曲线[5],由于混凝土达到峰值应力后的下降段在有限元软件分析中体现不明显,为增强ANSYS非线性迭代运算收敛性,不考虑超过峰值应力后的下降段,采用水平直线形式[6]。

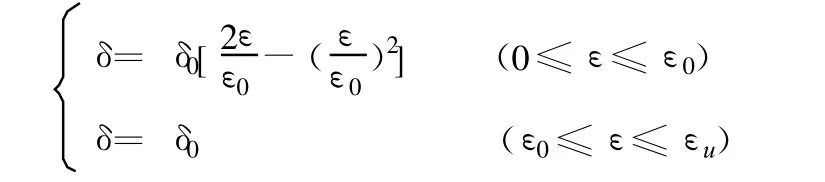
式中:δ为混凝土相应于应变ε的应力;ε0为对应于混凝土圆柱体抗压强度fc′(fc′=0.8fcu)[7]的峰值应变,结合我国研究成果取值0.002;根据Hognested 建议:δ0=0.85fc′,混凝土极限应变εu取值为0.0038。ANSYS中应力应变关系是拉压相等的,但由于混凝土抗拉强度很低,受拉段非常短,故可认为此设定对混凝土受拉时实际影响很小。

1.3.2 钢筋本构关系

钢筋屈服前,为理想弹性材料fy=Esεs;屈服后应力应变关系为平缓的斜直线,强化模量E′s=0.01Es,这样钢筋应力和应变有一一对应关系,便于后处理中观察钢筋的屈服和强化程度。

1.3.3 CFRP本构关系

CFRP为理想线弹性材料,超过极限抗拉强度将被拉断破坏 :δcf=Ecfεcf

1.4 屈服准则

混凝土屈服准则采用多线性随动强化模型(MKIN);钢筋采用双线性随动强化模型(BKIN),屈服准则设定后,相应的流动法则和硬化法则也由程序随之确定。

1.5 混凝土破坏准则

采用Willam-Warnke五参数破坏准则,假定破坏时,混凝土塑性变形已完成,塑性只能发生在W-W五参数准则定义的破坏面以内,一旦超出破坏面,材料将破坏。在低围压状态下,设置混凝土张开裂缝传递系数为0.5,闭合裂缝传递系数为 1.0,单轴抗拉强度ft=2.79MPa(ft=0.395fcu0.55)[7],受拉开裂后刚度折减系数为0.6,关闭压碎检查以增强非线性计算的收敛性[8]。

1.6 有限元模型的建立

由于混凝土和钢筋之间滑移很小,混凝土、CFRP之间的破坏形式通常是表层混凝土剥离或者CFRP发生局部断裂,因此假定混凝土和钢筋、混凝土和CFRP之间粘结足够,无相对滑移,采用共用节点方式来满足变形协调条件。混凝土网格尺寸划分为横截面5 cm×5 cm,沿梁纵向尺寸为7.5 cm。膜单元Shell41在大应变非线性分析时要求被划分为三角形单元,利用梁底节点生成CFRP三角形单元。为节省计算时间,利用对称约束建立1/2梁进行分析,建成后的有限元模型如图2示。

图2 CFRP加固RC梁有限元模型

1.7 利用单元生死进行不同工作状态模拟

CFRP实际加固应用中,由于种种条件限制,往往不能完全卸除荷载后进行加固。CFRP通常在不卸载情况下直接粘贴在构件表面,这样CFRP的初始应变为0,初始工作应力也为0,CFRP只能随着被加固构件变形的进一步开展而发挥作用,即存在所谓“二次受力”问题。ANSYS要求必须在前处理器一次性建好模型,因此利用单元生死技术,在第一载荷步先把Shell41单元全部杀死后施加荷载,相当于构件在没有加固的情况下工作,待施加到预定荷载后再激活这些单元,以此来模拟二次受力问题。而始终不杀死Shell41单元相当于不考虑“二次受力”时的情况。第一载荷步杀死Shell41单元后不再激活相当于不进行加固的对比梁情况。

2 计算结果分析

对不进行加固的对比梁B1、不考虑二次受力的CFRP加固梁B2、加载100 kN后再进行CFRP加固即考虑二次受力的梁B3,分别逐级施加集中荷载。在一般区段加载幅度为20 kN,开裂区段与屈服阶段加载幅度为10 kN。开裂荷载通过混凝土分布裂缝的出现情况与荷载挠度曲线的变化综合判定,屈服荷载根据受拉钢筋的应力值判定。临近破坏时加载幅度为1 kN,最后一次收敛解被认定为极限荷载。

如图3所示,在初始加载阶段,梁 B1～B3挠度随着荷载的增长线性增长,初始抗弯刚度相同。在达到混凝土开裂荷载40 kN后,梁B1～B3抗弯刚度下降,挠度增长的斜率减小,但抗弯刚度差别仍不大。随着荷载进一步逐级加大,抗弯刚度分化逐步显现,抗弯刚度依次B2＞B3＞B1。在达到屈服荷载150 kN后,梁B1随着钢筋的屈服,中和轴迅速上升,压区高度减小,最后在荷载增大不多的情况下,挠度急剧增长,混凝土受压破坏,极限荷载为184 kN,挠度值为20.59 mm。由于CFRP的存在,梁B2极限荷载为240 kN,挠度值为30.29 mm,梁B3极限荷载为219 kN,挠度值为25.31 mm。梁B2、B3较梁B1极限承载力分别增长了30.4%和19.0%,破坏时的挠度分别增长了47.1%和22.9%。相对于二次受力梁B3,不考虑二次受力的梁B2较B3极限荷载和破坏时的挠度分别增长了9.6%和19.7%。

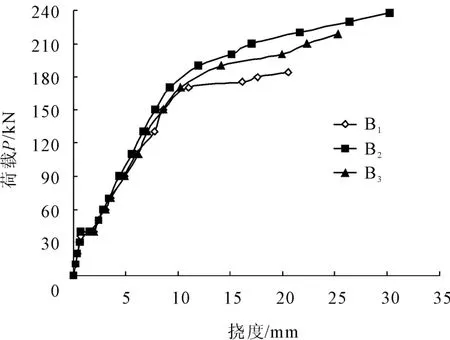
图3 梁 B1～B3荷载-挠度

如图4所示,在混凝土开裂前,梁 B1～B3受拉钢筋应力呈线性增长。在混凝土开裂退出工作后,梁B1、B3混凝土承担的拉应力随即由钢筋承担,梁B2拉应力由钢筋和CFRP共同承担,受拉钢筋应力有平台状突变。混凝土开裂后,钢筋应力增长速度加快。由于CFRP的存在,梁B2钢筋应力增长滞后于梁B1,梁B3由于CFRP在加载100 kN后才参加工作,前期钢筋应力增长与梁B1差别不明显。在达到屈服荷载后(梁B1～B3屈服荷载稍有差异,依次 B2＞B3＞B1),钢筋均进入流塑状态,此时CFRP能继续承担拉应力,延缓了中和轴急剧上升导致的压区混凝土压溃,梁B2、B3钢筋的屈服和强化程度更为充分(B2＞B3＞B1)。

图4 梁 B1～B3荷载-钢筋应力

如图5所示,梁B2CFRP应力在混凝土开裂前线性增长。随着混凝土开裂,由于混凝土拉应力发生了转移,CFRP应力有平台状增长。随后,CFRP应力增长速度加快。在钢筋屈服后,梁B2、B3CFRP应力均大幅度增长。破坏时,梁 B2、B3CFRP工作应力分别是2 650MPa、2 060MPa,均未达到碳纤维布的极限拉应力,分别为极限拉应力的72.9%和56.7%。

对于实际试验结果[1],梁 B1、B3(未有对应梁 B2的试验)极限荷载分别为185 kN、240 kN,破坏时挠度值分别为16.3 mm和19.1 mm,有限元分析与试验结果的荷载挠度曲线吻合,极限荷载误差分别为0.5%和8.8%。分析主要原因为:①有限元模型本构关系及各参数设定与实际情况尚存在差异;②有限元非线性运算收敛较困难导致了提前发散;③单个实际试验随机性因素造成的离散性。

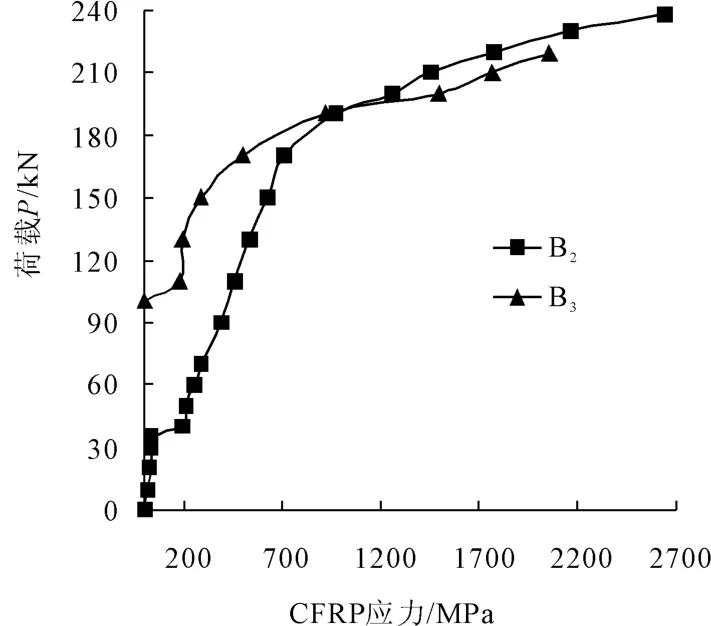
图5 梁B1～B3荷载-CFRP应力

3 结 论

(1)在钢筋屈服后,由于CFRP能继续承担拉应力,延缓了中和轴急剧上升导致的压区混凝土压溃,因而CFRP加固钢筋混凝土梁在后期抗弯刚度、延性和极限承载能力方面均有一定增强。

(2)在结构承受较大初始荷载情况下,二次受力问题对加固梁的抗弯刚度、极限承载能力、延性均存在一定影响。但由于CFRP是在钢筋进入屈服阶段,应力停止增长后才发挥巨大作用,因而二次受力时的加固也能取得较好效果。

(3)有限元数值仿真分析与实际试验结果吻合较好,有限元分析方法可掌握各材料的全程工作状态,并节约试验经费,用于该领域的科学研究是可行的。

[1]赵丹丹.碳纤维布及高强钢绞线网加固钢筋混凝土梁的试验研究[D].兰州理工大学,2008.

[2]GB50010-2002.混凝土结构设计规范[S].北京:中国建筑工业出版社,2001.

[3]中国工程建设标准化协会.碳纤维片材加固混凝土结构技术规程[S].北京:中国计划出版社,2003.

[4]ANSYS,Inc.Release 10.0 Documentation for ANSYS[R].2005.

[5]江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005:47-48.

[6]王勃,付德成,尹新生.FRP加筋混凝土梁受弯性能有限元分析[J].混凝土,2008,(5):13-15.

[7]腾智明,朱金铨.混凝土结构及砌体结构(上册)[M].北京:中国建筑工业出版社,2003:12,16.

[8]李围,叶裕明,刘春山,等.ANSYS土木工程应用实例(第二版)[M].北京:中国水利水电出版社,2007:81-83.

Nonlinear Finite Element Analysis on Flexural Performances of RC Beams Strengthened with CFRP Sheets

YU Long1,2
(1.College of Civil Engineering,LanzhouUniversity of Technology,Lanzhou,Gansu730050,China;2.Zhengzhou Guancheng Construction&Development Chief Corporation,Zhengzhou,He'nan450053,China)

In order to thoroughly comprehend the theory and performance of CFRP reinforcement,it is significant to study the different stress states of concrete,reinforcement bar and CFRP from cracking,yielding to destrorying.Here,the finite element models for flexural RC beams strengthened with CFRP sheets are created through ANSYS software,the different work ways of CFRP are simulated with element birth and death technology,and the nonlinear finite element analysis are made for the beams from cracking and yielding to destrorying.The results show that after yielding of the reinforcement bar,the late bending rigidity,ductility and ultimate bearing capacity of the beams are all strengthened.When the initial load is big,the secondary load could influence the performances of CFRP reinforcement on all aspects as mentioned above.It is only on the yielding stage of the reinforcement bar that CFRP could produce its huge action of reinforcement,therefore,the reinforcement of secondary load can also be effective.The analytic results tally with the actual experiment data.

CFRP;RCbeam;nonlinear finite element analysis;secondary load;element birth and death

TU375.1

A

1672—1144(2010)02—0113—04

2010-01-07

2010-02-20

于 龙(1973—),男(汉族),河南郑州人,工程师,硕士研究生,主要从事大跨空间及混凝土结构方面的研究。