Zernike多项式在拟合光学表面面形中的应用及仿真

杨佳文 黄巧林 韩友民

（北京空间机电研究所,北京 100076）

1 引言

光学主反射镜是空间光学遥感器的重要组成部分,它的镜面面形精度是影响空间光学遥感器分辨率的重要因素之一。在地面装调过程中,反射镜在光轴水平和光轴竖直两种状态下,由于重力场的作用,反射镜的镜面将会发生变形,因此在进行光学反射镜设计时需要做镜面变形分析,用以检验所设计的光学反射镜是否满足面形精度要求。镜面变形包括刚体位移和表面变形,刚体位移会引起光学系统像倾斜、离轴和离焦,表面变形将影响光学系统的波前差。刚体位移可以通过调整光学元件之间的相对位置来消除,而表面变形无法消除。因此镜面变形中的表面变形能够真实反映光学反射镜的面形精度[1-2]。本文以自由曲面镜面为例,通过有限元分析得到面形数据,用泽尼克（Zernike）多项式对变形后的面形进行精确拟合,并分离出刚体位移部分得到表面变形云图,计算出表面变形的表面变形均方根（RMS）和表面变形最大值与最小值之差（PV）。

2 Zernike多项式

理想的光学镜子表面是光滑而连续的,而从有限元软件中提取的变形数据是离散的,将离散的变形数据拟合成光滑连续的曲面称为镜面拟合。有很多方法可以用于镜面拟合,如最小二乘法、Gram-Schmidt方法、协方差法和SVD法,最理想的一种方法是Zernike多项式法,Zernike多项式对于拟合镜面面形具有如下优点[3]:

1）在单位圆上正交。函数系的正交使不同多项式的系数相互独立,对消除偶然因素的干扰很有利;

2）Zernike多项式容易与Seidel像差项对应,为有选择地单独处理各像差系数、优化系统性能提供了有效方法;

3）Zernike多项式各项物理意义明了,是结构分析与光学分析程序之间的接口工具[4]。

在直角坐标系下N项Zernike多项式为:

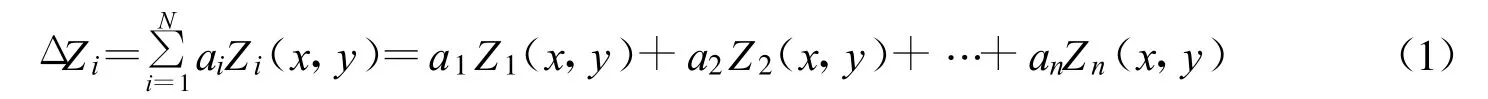
式中 ai为Zernike多项式中第i项系数;Zi为Zernike多项式的第i项;N为Zernike多项式的项数;x,y为数据点的坐标值。

一般该表达式取到28项就足够精确,因此,本文取28项多项式对镜面面形进行拟合。Zernike多项式各项在直角坐标系中的表达式如表1所示[5]:在有限元软件中对光学反射镜进行静力分析后,可以得到镜面变形输出文件,输出文件中的数据包括:镜面上各节点变形前的坐标值 xi、yi、zi,（i=1,2,3,…,m）,各节点变形后与变形前的坐标差值Δxi、Δyi、Δ zi,（i=1,2,3,…,m）,m 为镜面节点个数。设有限元模型中光轴方向为z轴,则将 xi、yi、Δ zi带入N项Zernike多项式中得到:

表1 直角坐标系中Zernike多项式各项表达式

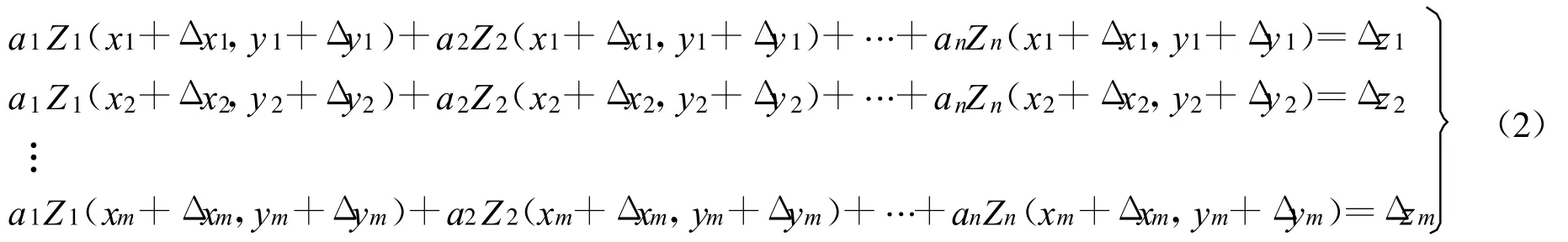
令zij=Zj（xi+Δ xi,yi+Δ yi）,（i=1,2,3,…,m;j=1,2,3,…,n）,即第 i个点的第j项Zernike表达式赋值给zij,则上式可简记为:

式中 Z=（zij）为 m ×n 矩阵;A=（a1,a2,…,an）T;Z′=（Δ z1,Δ z2,…,Δ zm）T。

3 Zernike多项式拟合镜面面形的仿真流程

镜面面形的计算机仿真流程如图1所示。首先在有限元分析软件MSC.Patran中建立光学反射镜模型,并对光学反射镜模型在光轴水平和光轴竖直两种状态下分别进行静力分析,将分析获得的光学表面数据文件输出到Matlab软件中,编程实现Zernike多项式拟合面形[6]。

图1 镜面面形的计算机仿真流程图

根据所有节点变形后的坐标,利用Zernike多项式拟合出变形后的面形（如图2所示）,并去除掉镜面的刚体位移,得到只含有表面变形的镜面面形,计算变形后的节点到这个拟合曲面在光轴方向的距离[7]。

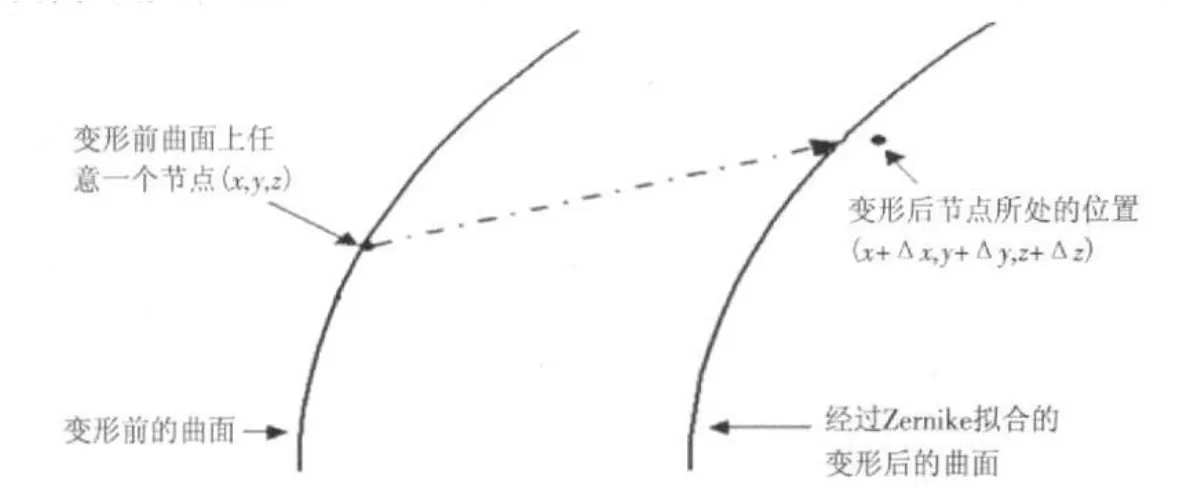
图2 镜面变形图

最后,根据公式（4）、（5）计算出面形RMS值和PV值,并绘出镜面面形云图。

式中 xi为变形后的节点到拟合曲面的距离为所有变形后的节点到拟合曲面的平均距离;N为节点个数。

4 Zernike多项式拟合光学反射镜面形的实例

本文对光学非球面反射镜进行镜面的Zernike多项式拟合,反射镜采用蜂窝夹心轻量化形式,支撑方式为背部六点支撑,主要尺寸见表2。反射镜材料参数见表3。

表2 反射镜结构参数mm

表3 反射镜材料参数

在有限元分析软件MSC.Patran中用板单元建立几何模型、划分网格,并进行静力分析[8～9]。反射镜有限元模型及其内部结构如图3所示:

图3 反射镜有限元模型及其内部结构

采用有限元分析软件MSC.Nastran对模型进行静力分析,得到光轴水平和光轴竖直状态的镜面面形云纹图,如图4所示。从图4（a）中可以看到在光轴水平状态下反射镜镜面产生了刚体平移和刚体的倾斜;图4（b）中光轴竖直状态镜面面形只有重力方向的刚体平移,没有产生刚体的倾斜。

有限元分析后将镜面变形数据文件输出,利用Matlab软件强大的数据处理能力,编程实现Zernike多项式拟合面形。并将镜面的刚体平移、倾斜与表面变形分离,最终得到去除刚体平移、倾斜后的镜面RMS值、PV值。图5、6、7分别表示反射镜光轴水平状态Zernike多项式拟合面形、反射镜光轴水平状态下镜面的刚体位移和倾斜、反射镜光轴水平状态下去除刚体位移后的镜面面形。

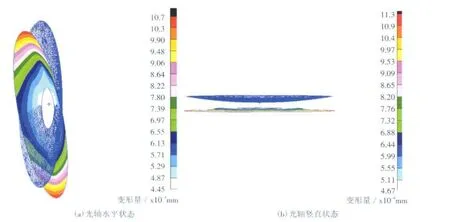
图4 反射镜镜面面形云纹图

图5 反射镜光轴水平状态Zernike多项式拟合面形

图6 反射镜光轴水平状态下镜面的刚体位移和倾斜

由图7可知,反射镜光轴水平状态时,由于采用背部六点支撑,重心与支撑点不在一个平面内,会产生力矩,因此,在光轴水平状态下反射镜镜面产生了明显的刚体平移和刚体倾斜。

图8、9、10分别表示反射镜光轴竖直状态Zernike多项式拟合面形、反射镜光轴竖直状态镜面的刚体位移、反射镜光轴竖直状态去除刚体位移后的镜面面形。

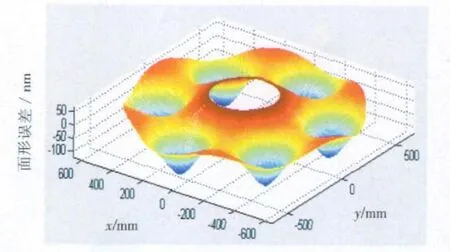
图8 反射镜光轴竖直状态Zernike多项式拟合面形

图9 反射镜光轴竖直状态下镜面的刚体位移

图10 反射镜光轴竖直状态下去除刚体位移后的镜面面形

从图10可看出,反射镜在光轴竖直状态下的镜面变形包括镜面的刚体位移和表面变形,而没有刚体倾斜。

表4 仿真分析结果 nm

表4列出了反射镜在光轴水平和光轴竖直状态下去除刚体位移前后的镜面面形RMS值和PV值。对仿真结果进行分析可以看出反射镜光轴水平状态时的刚体位移和倾斜量较大,计算镜面面形时,若不将其与表面变形分离,计算出的RMS值和PV值误差很大,而反射镜光轴竖直状态下刚体位移量很小,可以忽略不计,去除刚体位移前后镜面面形基本没有改变。另外,反射镜有限元模型网格的疏密在一定程度上对Zernike多项式拟合的精度也有影响:网格尺寸较大,则镜面网格数据量小,拟合精度较低;网格尺寸小,虽然可以提高拟合精度,但会大大增加有限元计算和面形拟合的时间。因此,网格尺寸应是在满足拟合精度的条件下尽量大为宜。

5 结束语

本文介绍了Zernike多项式及其在计算机仿真分析中拟合非球面镜面面形的一种方法,并举例分析了反射镜在光轴水平和光轴竖直两种状态下的镜面变形,得到了去除刚体位移前后的镜面面形的可视化分析结果,为今后进一步设计满足一定面形精度要求的大口径轻量化反射镜提供了有力保证。

[1]王栋,杨洪波,陈长征.光学表面面形的计算机仿真[J].计算机仿真.2007,24（2）:298-300.

[2]毕勇,翟嘉,吴金虎,等.一种光学仪器镜面面形的处理方法[J].光学技术.2009,35（1）:10-12.

[3]单宝忠,王淑岩,牛憨笨,等.Zernike多项式拟合方法及应用[J].光学精密工程.2002,10（3）:318-323.

[4]吴清文.镜面面型误差的曲面方程处理方法[J].光学精密工程,1998,6（6）:56.

[5]屈金祥.Zernike多项式及其在低温光学中的应用[C].上海市制冷学会二○○五年学术年会论文集,2005:69-72.

[6]谢晋,郭家隆.基于Matlab软件对曲面方程已知的曲面面形误差求解与分析[J].机械设计与制造.2008,1（1）:81-83.

[7]Juergens R C,Coronato P A.Improved Method for Transfer of FEA Results to Optical Codes[J].SPIE,2003,5174:105-115.

[8]Patrick A,Coronato R,Juergens C.Transferring FEA Results to Optics Codes with Zernikes:A Review of Techniques[J].SPIE,2003,5176:1-8.

[9]Chrzanowski C,Frohlich C,Shirgur B.Design and Structural/OpticalAnalysis of A Kinematic Mount for the Testing of Silicon Carbide Mirrors at Cryogenic Temperatures[J].SPIE,2004,5528:204-214.