遥感卫星立体影像传感器模型综述

李晨曦

（北京空间机电研究所,北京 100076）

1 引言

高分辨率遥感卫星的出现,使得利用卫星遥感立体影像实现地面目标的高精度定位与大比例尺测图成为可能。传感器成像几何模型的建立是进行地面目标定位和大比例尺测图的基础,它反映了地面点的三维空间坐标与相应像点在像平面坐标系中二维坐标之间的数学关系。

遥感卫星立体影像传感器模型主要可以分为以下两大类:

1）物理传感器模型,又称严密传感器模型。考虑成像时造成影像变形的物理参数如地表起伏、大气折射、相机摄影参数以及卫星的位置、姿态变化等,然后利用这些物理条件构建成像几何模型。通常这类模型的数学形式较为复杂且需要完整的传感器信息,但由于其在理论上是严密的,因而模型的定位精度较高。

2）通用传感器模型。不考虑传感器成像的物理因素,直接采用数学函数如多项式、直接线性变化方程式以及有理函数多项式等形式来描述地面点和相应像点之间的几何关系。这类方法与具体传感器无关,数学模型形式简单、计算速度快,但属于不甚严密的表达方式。

以下将选择几种具有代表性的主流传感器模型进行详细分析。

2 严密传感器模型

严密传感器模型是在已知相机或传感器位置和方位的条件下,采用严密的几何变换,建立像点坐标与相应的地面点三维空间坐标关系的模型[1]。在这类传感器模型中,最具有代表性的是以摄影测量学中的共线方程为基础的传感器模型。

目前绝大部分遥感卫星均采用线阵CCD作为成像器件,通过推扫成像的方式获取立体影像,如图1所示。相机在每一个成像时刻是中心投影,得到一行线影像,一幅影像由若干行线影像构成,形成一个多中心投影方式。

图1 线阵CCD传感器成像方式

根据共线方程,该影像第i扫描行上任一像点坐标与其对应地面点三维空间坐标满足以下关系式:

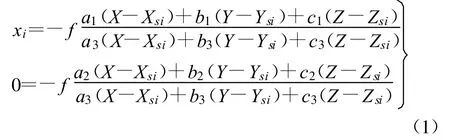
式中 （xi,0）为第i扫描行上像点的像平面坐标;（X,Y,Z）为其对应地面点三维空间坐标;f为相机主距;（Xsi,Ysi,Zsi）为第 i扫描行的摄站坐标;（ai,bi,ci）为旋转矩阵中的元素,由第i扫描行的外方位角元素（φi,ωi,κi）确定,具体关系参阅文献[2]。

在已知相机具体参数和摄影时刻星历轨道、姿态信息的情况下,将像点坐标代入式（1）中即可求出相应地面点三维空间坐标。由于共线方程是按照严格几何投影关系得到的物象关系式,因此基于共线方程的严密传感器模型在理论上是严密的,对卫星影像的处理精度很高。

线阵CCD推扫式影像是行中心投影影像,即同一扫描行上的像点具有相同的外方位元素,不同扫描行之间的像点具有不同的外方位元素,由于这一动态特性导致影像的严密传感器模型十分复杂。以IKONOS卫星影像为例,其严密传感器数学模型文件长度达183页,相应的接口控制文件达到225页[3],用商业后处理软件实现这一严密模型是不现实的;同时,相机的具体参数和摄影时刻星历轨道、姿态等信息对于普通用户都是保密的。因此基于共线方程的严密传感器模型虽然对卫星影像的处理精度高,但并不是普通用户可以建立的,一般由传感器研制方或遥感影像处理单位以严密传感器模型为基础,开发专业的影像处理软件,用于对卫星影像进行几何校正。如Gruen A等人开发的针对日本ALOS卫星影像处理的SAT-PP软件,对ALOS卫星全色影像处理精度高程中误差小于2.49m,平面中误差在5.5m至6.6m之间[4],明显优于标称15m的CE90的平面精度和6m的LE90的高程精度。Konecny G等人于1987年开发了以严密传感器模型为内核的遥感影像处理软件—BLASPO[5],利用该软件对MOMS-2卫星影像[6]、SPOT和IRS-1C卫星影像[7]、IKONOS和Quickbird卫星影像[8]、SPOT5/HRS卫星影像[9]均取得了很高的处理精度。

基于共线方程的遥感卫星立体影像严密传感器模型理论严密,校正精度高,但前提是必须已知摄影时刻的轨道星历、姿态信息和传感器详细参数,在实际应用中往往无法得到这些参数;而且这种模型形式复杂,解算时运算量大,这也是选择该模型处理遥感影像时需要注意的问题。

3 基于仿射变换的传感器模型

基于仿射变换的传感器模型是通用传感器模型的一种。某些遥感影像的摄影高度大、视场角较小,以1999年美国发射的IKONOS卫星为例,其搭载的1m分辨率全色相机,焦距10m,视场角仅为0.93°。因此影像的外方位各元素之间往往存在着很强的相关性,这会影响解算外方位元素的稳定性,导致对遥感影像处理精度不高。在这种情况下,Okamoto于1981年提出了一种基于仿射变换的传感器模型[10],Snsumu Hattori与Tetsu Ono进一步研究与应用了该模型[11-12]。这种模型是建立在“小视场角内的中心投影近似于平行光投影”的假设基础上,即认为线阵CCD推扫式影像每一行影像的投影中心具有相同高度,投影中心平行,同时认为推扫是匀速的。我国张剑清教授对该模型进行了进一步的探讨[13],在这种假设前提下,通过一系列几何投影及仿射变换,得到像点坐标与相应地面点三维空间坐标数学关系如下:

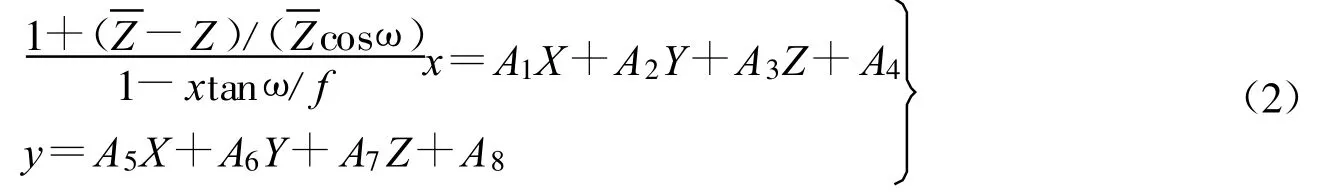
式中 （x,y）为像点坐标;（X,Y,Z）为相应地面点三维空间坐标;f为相机焦距为摄影区域地面平均高度;ω为对非星下点区域成像时相机光轴与星下点方向夹角;Ai（i=1,2,3,…,8）为待求系数。

Fraser等人于2001年成功地将基于仿射变换的传感器模型应用于IKONOS卫星影像,在补偿了由地球曲率引入的高度误差之后,定位精度可达1m[14]。该模型应用于法国SPOT卫星level1、level2立体影像[15],以及德国MOMS/2P卫星立体影像[16]处理,均取得了较好的定位精度。

基于仿射变换的遥感卫星立体影像传感器模型考虑了侧偏角、近似平行投影、地形起伏等因素,在不知道传感器详细参数的情况下,只需要少量地面控制点即可进行较高精度的卫星影像的空间定位,这是它的优势。然而这种模型也存在着一定的局限性,由于其假设“小视场角内的中心投影近似于平行光投影”,因此不适用于处理大视场角传感器影像,通用性较差。

4 基于直接线性变换的传感器模型

直接线性变换（Direct Linear Transformation）是一种直接建立像点坐标与地面点三维空间坐标关系的一种数学变换式。基于直接线性变换的传感器模型属于通用传感器模型的一种。其像点坐标与地面点三维空间坐标数学关系如下:

式中 （x,y）为像点坐标;（X,Y,Z）为相应地面点三维空间坐标;Li（i=1,2,3,…,11）为DLT系数。

只要已知6个地面控制点,将相应的像点坐标、地面点三维空间坐标代入式（3）,即可得到12个方程,从而求解L1～L11的11个系数,得到基于直接线性变换的遥感卫星立体影像传感器模型。

由式（3）可以看出,基于直接线性变换的传感器模型完全不需要已知传感器的任何参数,同样也不需要确定卫星星历、姿态等信息。其对卫星影像的处理精度完全依赖于所选择地面控制点的精度。

El-Manadili.Y等人于1996年使用基于直接线性变换的传感器模型对法国SPOT卫星影像进行了几何精度校正[17],Savopol等人于1998年将该模型应用于印度IRS-1C卫星影像的三维重建[18]。

实际上,由于基于直接线性变换的遥感器模型与严密传感器模型间存在直接关系,因此基于直接线性变换的遥感器模型经常应用于近景摄影测量中对摄影相机内方位元素的标定[19]。在已知DLT系数的情况下,摄影相机内方位元素的计算公式如下:

式中 （x0,y0）为相机的主点位置坐标;fx、fy分别为使用x方向和y方向像点坐标计算得到的相机主距;f为相机主距平均值。

基于直接线性变换的遥感卫星立体影像传感器模型对卫星影像进行处理时无需传感器参数以及卫星星历轨道、姿态等信息,具有表达式简单、解算简便、需要控制点数目少、无需初始值等优点,广泛应用于近景摄影测量和卫星影像的解析定位。这种模型的缺点是没有考虑影像外方位元素随时间变化的特点,将动态推扫式影像等同于静态画幅式影像进行处理,且没有考虑地表起伏等因素,导致处理精度的下降。

5 基于有理函数的传感器模型

高分辨率卫星成像过程中繁琐的姿态控制导致影像的严格几何模型形式极其复杂,要利用其提取地球空间三维信息,需要在向用户提供影像的同时把卫星详细的轨道星历、传感器成像参数和成像方式等信息一并交付,并且,最终用户需要具有摄影测量的专门知识和相当专业、复杂的应用处理软件。为了降低对用户专业水平的要求,同时保护卫星的核心技术参数不被泄露,某些厂家开始向用户提供一种与传感器无关的通用模型——基于有理函数的传感器模型。基于有理函数的卫星立体影像传感器模型是目前应用最为广泛且定位精度最高的通用传感器模型。

有理函数模型（Rational FunctionModel,RFM）是将像点坐标表示为以相应地面点三维空间坐标为自变量的多项式的比值,利用有理函数逼近二维像平面与三维物空间的对应关系。有理函数的一般形式如下:

其中 （u,v）为像点坐标;（X,Y,Z）为相应地面点三维空间坐标;aijk,bijk,cijk,dijk被称为有理函数系数（Rational Function Coefficient,RFC）。

有理函数可取不同的次数,式（5）中每一项的各个坐标分量（X,Y,Z）的次数最大不超过3,每一项各个坐标分量的次数的总和也不超过3（通常有1,2,3三种取值）。另外,分母项p3和p4的取值可以有两种情况:p3=p4（可以是一个多项式也可以是一个常量1）;p3≠p4。在模型中由光学投影引起的误差表示为一阶多项式,而地球曲率、大气折射及镜头畸变等引起的误差,可由二阶多项式趋近。高阶部分其他未知误差可由三阶多项式模拟。

有理函数次数越高,待求的有理函数系数越多,需要的地面控制点数目也就越多。以p3（X,Y,Z）=p4（X,Y,Z）且为3次多项式为例,共有60个待求有理函数系数,则至少需要30个地面控制点才能求解这些未知参数,并且要求控制点在物空间平面和高程范围内均匀分布。

基于有理函数的传感器模型最初应用于IKONOS卫星影像处理。Space Imaging公司在出售卫星影像的同时,向客户提供用于构建有理函数模型的参数文件,文件中共包含90个卫星影像参数,其中80个为有理函数系数,10个为规格化参数。由这90个参数就可以构建IKONOS卫星影像的有理函数模型,从而对卫星影像进行处理。张永生等人的实验证明,使用Space Imaging公司提供的有理函数传感器模型对IKONOS卫星影像进行处理,X、Y方向最大定位误差分别为9.656m和-5.981m,高程最大定位误差为11.373m;X、Y方向中误差分别为6.702m和3.684m,高程中误差为8.531m,明显优于标称的25m CE90的平面精度和12m LE90的高程精度[20]。

随着基于有理函数的传感器模型成功应用于IKONOS卫星影像处理,为实现商业利益最大化并保证传感器核心信息不外泄,越来越多的卫星厂家开始采取不公布传感器详细信息,只提供卫星影像有理函数模型的销售策略,如印度IRS-P5卫星、韩国KOMPSAT-2卫星、美国World View-1/2卫星等。目前国际上遥感影像商业处理软件主要有ENVI、PCI、ERDAS等,这几种软件以兼容多种卫星影像且处理精度高而著称。它们对遥感影像处理的核心思路就是通过建立相应卫星影像的有理函数传感器模型,从而实现高的影像处理精度。这也从一个侧面说明与其他通用传感器模型相比,基于有理函数的遥感卫星立体影像传感器模型在通用性、处理精度等方面都有着无可比拟的优势。

朱述龙等人利用不同的传感器模型分别对同一地区的SPOT卫星全色影像进行处理,得到如表1的结果[21]:

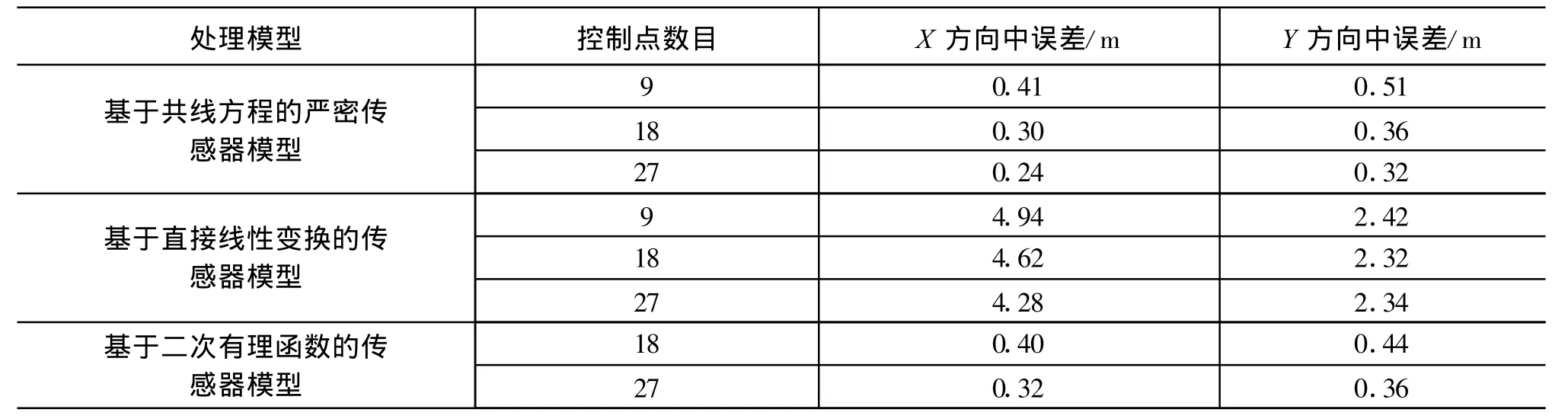
表1 SPOT卫星影像处理精度

由比较结果也可以看出,基于共线方程的严密传感器模型对卫星影像的处理精度最高,控制点的定位精度达到子像元级;基于有理函数的传感器模型的处理精度接近基于共线方程的严密传感器模型的精度;基于直接线性变换的传感器模型处理精度最低。

6 结论

通过以上的研究分析可以得到如下结论:

1）基于共线方程的严密传感器模型理论严密,对卫星影像的处理精度最高,是对卫星影像进行几何校正极好的工具。但建立模型需要传感器具体参数以及卫星星历轨道、姿态信息,对普通用户来说有一定难度,且数学形式复杂,解算运算量大,一般商业卫星影像处理软件无法实现,需开发专用软件。

2）与严密传感器模型相比,通用传感器模型具有不需要传感器详细参数及卫星星历轨道、姿态信息、数学形式相对简单、模型与具体传感器无关等优点,但由于模型在理论上不甚严密,导致其对影像的处理精度低于严密传感器模型的处理精度。

3）通用传感器模型中,基于有理函数的传感器模型对卫星影像的处理精度最高,在选择合理分布的地面控制点情况下,其处理精度接近基于共线方程的严密传感器模型处理精度。这种模型是目前国际上应用最广泛的一种遥感卫星立体影像处理模型。但与其他通用传感器模型相比,其数学形式较为复杂,需要较多的地面控制点进行解算。基于直接线性变换的遥感器模型对影像处理精度低,其优势是完全独立于具体的传感器及卫星星历轨道、姿态信息,只需要少量地面控制点即可以进行解算。在未知任何传感器及卫星星历轨道、姿态信息仅有卫星影像的前提下,基于直接线性变换的传感器模型不失为一种选择。

4）基于仿射变换的传感器模型在处理长焦距小视场角的传感器获得的影像时能得到较好的处理精度,但其通用性差,对于大视场角卫星影像不适用。

在对遥感卫星立体影像进行处理时,可综合考虑处理精度、模型复杂程度、对已知数据要求等多方面因素,选择适当的处理模型。

[1]张永生,巩丹超,刘军,等.高分辨率遥感卫星应用（成像模型、处理算法及应用技术）[M].北京:科学出版社,2004.

[2]李德仁,王树根,周月琴.摄影测量与遥感概论[M].北京:测绘出版社,2008.

[3]陈闻畅.IKONOS成像机理及立体测图精度研究[D].武汉大学,2005.

[4]Gruen A,Kocaman S,Wolff K.Calibration andValidation of Early ALOS/PRISM Images[J].Journalof the JapanSociety of Photogrammetry and Remote Sensing,2007,46（1）:24-38.

[5]Konecny G,Kurck E,Lohmann P,et al.Evaluation of SPOT Imagery on Analytical Photogrammetric Instrument[J].PE&RS,1987,53（9）:1223-1230.

[6]Büyüksalih G,JacobsenK.Geometric Aspects of MOMS-2P Three-line-imagery for Mapping Applications[C].Annual Meeting of the Remote Sensor Society,Lancaster,UK,2000.

[7]Jacobsen K.Geometric Calibration of Space Remote Sensing Cameras for Efficient Processing[J].IAPRS,1998,32（Part 1）:33-43.

[8]Jacobsen K,Konecny G,Wegmann H,et al.High Resolution Sensor Test Comparison with SPOT,KFA1000,KVR1000,IRS-1C and DPA in Lower Saxony.IAPRS,2003,32（Part 4）:260-269.

[9]Jacobsen K.DEM Generation by SPOT HRS[J].IAPRS,2004,XXXV（Part B1）:439-444.

[10]Okamoto A.Orientation Theory of CCD Line-scanner Images[J].InternationalArchives of Photogrammetry and Remote Sensing,1988,27（part B3）:609-617.

[11]Hattori S,Ono T,Fraser C,et al.Orientation of High Resolution Satellite Images Based on Affine Projection[J].International Archives of Photogrammetry and Remote Sensing,2000,XXXIII（part B3）:359-366.

[12]Ono T,Hattoris,Hasegawa H,et al.Digital Mapping Using High Resolution Satellite Imagery Based on 2D Affine Projection Model[J].International Archives of Photogrammetry and Remote Sensing,2000,XXXIII（part B3）:672-677.

[13]张剑清,张祖勋.高分辨率遥感影像基于仿射变换的严格几何模型[J].武汉大学学报信息科学版,2002,27（6）:554-559.

[14]Fraser C S,Hanley H B,et al.Sub-meter Geopositioning with IKONOS GEO Imagery[C].Proceeding of ISPRS Workshop“High resolution mapping from space 2001”.18-21 September,Hanover,Germany.

[15]Okamoto A,Clive F,Hattori S,et al.An Alternative Approach to the Triangulation of SPOT Imagery[J].IAPR S,1998,32（Part B4）:457-462.

[16]Hattori S,Ono T,et al.OrientationofHigh-resolutionSatellite Imagesbased inAffine Projection[J].IAPRS,2000,33（Part B1）:359-366.

[17]El-Manadili Y,Novak K.Precision Rectification of SPOT Imagery Using the Direct Linear Transformation Model[J].PE&R S,1996,62（1）:67-72.

[18]Savopol F,Armenakis C.Modelling of the IRS-1C Satellite PAN Imagery Using the DLT Approach[J].IAPRS,1998,32（Part4）:511-514.

[19]冯文灏.近景摄影测量[M].武汉:武汉测绘科技大学,2000.

[20]张永生,刘军.高分辨率遥感卫星立体影像RPC模型定位的算法及其优化[J].测绘工程,2004,13（1）:1-4.

[21]朱述龙,史文中,张艳,等.线阵推扫式影像近似几何校正算法的精度比较[J].遥感学报,2004,8（3）:220-226.