熵权模糊数学方法在水质评价中的应用

王铁风 潘孝辉

水质综合评价中的污染程度、水质类别、分类界限等都是一些客观存在的模糊概念,因此,利用模糊数学理论,结合水质指标及其评价原理,利用水质污染程度由轻到重逐渐变化的模糊特性,相对于通用的综合污染指数P值法和W值水质评价法等确定性数学方法,可以获得更科学和更合理的评价结果。在水质模糊综合评价中,需确定影响水质的各主要因素,确定评价因子集、评价集、隶属函数,然后通过计算各因素的权重和隶属度,得到综合隶属度,确定水质级别。在模糊综合评价中,权重计算是一项重要的内容,对评价的结果有重要影响。目前最为常用的一种赋权方法是根据各单项指标对环境污染的贡献不同,采用离差权法(即污染物超标法)确定各评价指标的权重系数。但这种方法存在明显不足[1]:当存在多个评价对象时,每个评价对象都要分别计算一次在该对象下每个评价指标的权重值,工作量过大;计算得到的权重值仅考虑了个体因子的特征,而对多个评价对象的相互联系却无法描述。为了解决上述问题,可以引进熵的概念。熵本是热力学中的概念,后由申农(Shannon C.E.)引入信息论[2],现已在工程技术、社会经济、环境科学等领域得到广泛应用[3-7],取得了较好的效果。本文尝试将熵权法用于河流水质模糊综合评价中各因子的赋权,并应用该方法对上海长江口段的水质进行综合评价,以验证该方法的可行性。

1 熵权理论

信息量是信息论中的基本概念,申农(Shannon C.E.)于1948年提出了此概念,把熵的概念引入信息论使信息量化,从而使信息论产生了一次飞跃性的发展[2]。按照熵思想,人们在评价决策中获得信息的多少和质量,是决策的精度和可靠性大小的决定因素之一。同时用熵还可以度量信息量的多少。因此,可以用熵来确定权重。当评价对象在某项指标上的值相差较大时,熵值较小,说明该指标提供的有效信息量较大,该指标的权重也应较大;反之,若某项指标的值相差越小,熵值较大,说明该指标提供的信息量较小,该指标的权重也应较小。当各被评价对象在某项指标上的值完全相同时,熵值达到最大,这意味着该指标未向决策提供任何有用的信息,可以考虑从评价指标体系中去除[8]。在水质模糊评价中,通过对熵的计算确定权重,就是根据各项监测指标值的差异程度,确定各指标的权重。但需要说明的是,熵权并不是表示决策评估问题中某指标实际意义上的重要性系数,而是在给定评价对象集后各种评价指标值确定的情况下,各指标在竞争意义上的相对激烈程度。从信息角度考虑,它代表该指标在该问题中提供有效信息量的多寡程度[8]。

熵值赋权基本方法[8]。

设有m个评价指标,n个评价对象,则形成原始数据矩阵R′=(r′ij)m×n。

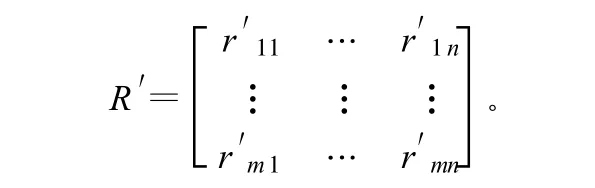
1)对原始数据矩阵进行标准化得到:

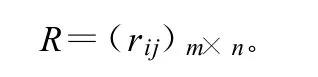
2)信息熵。在有 m个指标,n个被评价对象的评价问题中,第i个指标的熵定义为:

3)熵权。定义了第i个指标的熵之后,可得到第i个指标的熵权定义,即:

2 长江口水质模糊综合评价

2.1 建立评价因子集

按照一定的原则,从2005年上海市长江口6个监测断面的监测指标中选取具有代表性的DO,CODMn,CODCr,BOD5,N-NH3,TP六个指标作评价因子,组成评价因子集U:

上述六项监测指标在六个监测断面的监测数据见表1。

2.2 建立评价集

GB 38382-2002地表水环境质量标准[9]中根据地表水水域功能和保护目标,将地表水水质分成了五类,故确定评价集 V为:

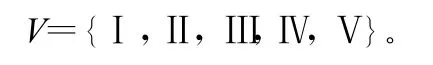
2.3 建立单因子隶属矩阵

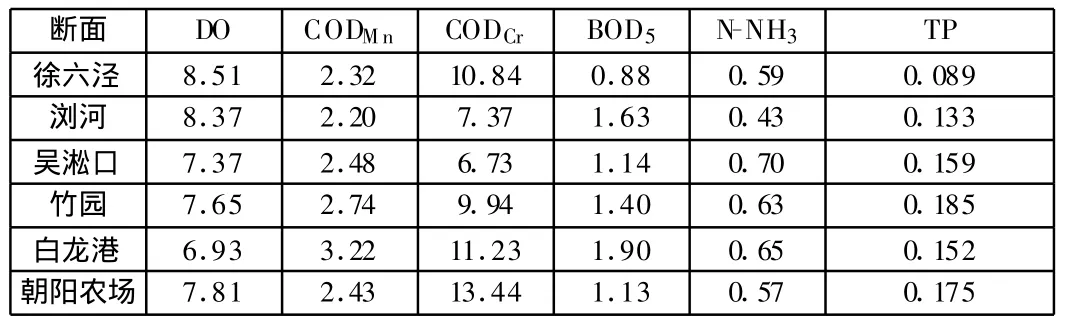
表1 2005年上海市长江口6个监测断面六项主要检测指标数值

根据GB 38382-2002地表水环境质量标准[9],确定各指标属于各水质级别的隶属函数,从而确定单因子隶属度,得到单因子评价矩阵A。以徐六泾监测断面为例,其隶属矩阵为:

限于篇幅,其他监测断面的隶属矩阵不一一列出。

2.4 权重计算

首先将监测数据构成的原始矩阵进行初始化,结果见表2。

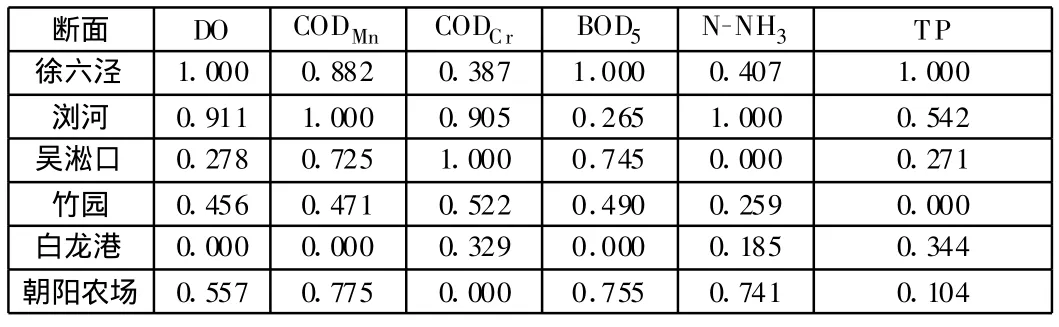
表2 原始数据初始化结果

数据经过整理后,根据熵权法公式计算出各评价指标的熵和熵权,结果见表3。

表3 各评价指标信息熵与熵权

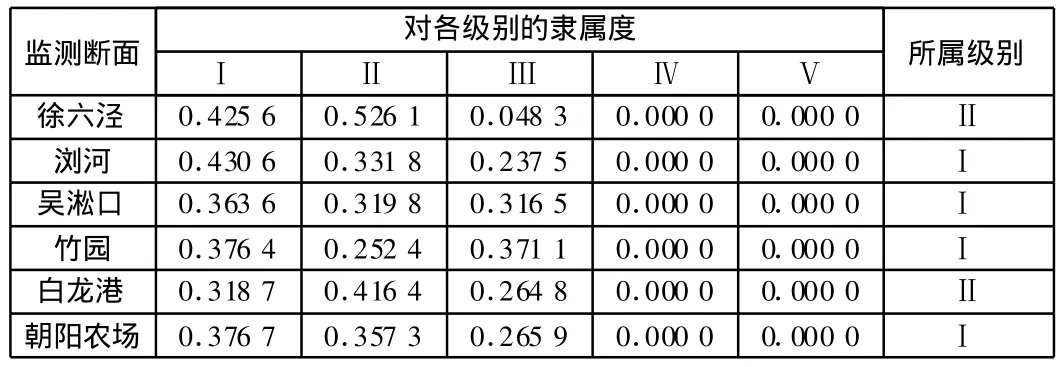
表4 综合评价结果

2.5 评价结果

综合评价结果见表4。利用熵权法赋权的模糊综合评价结果表明,长江口各监测断面的水质级别为Ⅱ级及以上,水体尚清洁,综合污染程度不严重。在各评价指标中总磷(TP)和氨氮(N-NH3)的权重较大,分别为0.354 5和0.268 4,说明长江口氮磷营养物污染所占比重较大(见表3)。为验证熵权法的有效性,本文还将熵权法与传统的模糊综合评价方法进行了对比(见表5)。结果表明,熵权法和传统的综合评价方法得到的评价结果基本一致。用传统方法确定的各评价因子权重见表6。根据传统的权重计算方法,以上6个监测点分别确定了6次权重。而且,同指标的监测值相近,确定的权重却有很大不同。如徐六泾和朝阳农场,氨氮(N-NH3)的监测值分别为0.59和0.57,确定的权重却分别为0.229 5和0.159 1,差别达44%,误差较大。

表5 评价结果对比

表6 传统赋权方法的赋权结果

3 结论

1)与传统的模糊综合评价方法相比,通过熵权法给各评价因子赋权,并对长江口6个监测点进行水质评价时,只需计算1次就能得到适用于所有点的权重,大大减少了评价工作所需的工作量。2)使用熵权法赋权,可将同一监测指标的多个监测样本点结合确定权重,考虑了多个样本间的联系,可削弱异常值的影响,使评价结果更准确、合理。3)实例计算结果表明,熵权法是一种比较有效的赋权方法,在水质模糊综合评价中有重要应用价值。

[1] 田景环,邱 林,柴福鑫.模糊识别在水质综合评价中的应用[J].环境科学学报,2005,25(7):950-953.

[2] Shannon.C.E.A mathematical theory of communication[J].Bulletin of System Technology Journal,1948,27(7):379-423.

[3] 周梅华.可持续消费测度中的熵权法及其实证研究[J].系统工程理论与实践,2003(12):25-31.

[4] 方大春,刘国林,张连蓬,等.信息熵在投资决策中的应用[J].价值工程,2004(2):115-117.

[5] 田启华,杜义贤.基于熵权模糊综合评判法的机械产品性能评价研究[J].中国制造业信息化,2004,33(3):97-99.

[6] 程 天,张彩香.基于熵权的模糊AHP法在填埋场选址中的应用[J].环境卫生工程,2003,12(2):64-67.

[7] 林运东,门宝辉,贾文善.熵权系数法在水体营养化类型评价中的应用[J].西北水资源与水工程,2003,13(3):27-28.

[8] 邱宛华.管理决策与应用熵学[M].北京:机械工业出版社,2002:193-196.

[9] GB 38382-2002,地表水环境质量标准[S].