基于马尔可夫过程与进步度的教学效果评价

高秀艳 ，刘 扬 ，张 欣 ，刘 英

（1.河北软件职业技术学院，河北 保定 071000；2.河北大学电子信息工程学院，河北 保定 071002）

在教师教学效果的评价过程中，由于存在学生基础水平差异及偶然性等因素，所以不能单纯依靠学生一次考试成绩的优劣来评价教师的教学效果。而在实际中，我们更希望能够预测一位教师将来的教学效果如何。教师的教学过程是随机过程，从动态角度看，一位教师的教学效果依赖于所教学生目前的状态，与以往所处的状态无明显或直接的关系，即具有随机性，符合马尔可夫过程的特点，因此用马尔可夫过程对其进行分析符合实际条件。目前，这项研究已经相对成熟且取得了较好的应用效果[1-4]。但这种分析方法是以长期教学过程后的平均分做为评价指标的，过分注重稳态下的结果，忽视了学生成绩的动态进步与退步。本文提出了利用马尔可夫过程理论对教学效果进行建模，并对所得到的转移概率矩阵进行分析，提出了进步矩与进步度的概念，使用进步度作为评价教学效果的新标准，省去了传统评价方法中计算特征方程解的过程，同时使评价结果更加直观和客观，计算更加简单。

1 马尔可夫过程基本理论

马尔可夫过程（Markov process）是一类随机过程。它的原始模型马尔可夫链，由俄国数学家A.A.马尔可夫于1907年提出。该过程具有如下特性：在已知目前状态(现在）的条件下，它未来的演变（将来）不依赖于它以往的演变（过去）。时间与状态均为离散的马尔可夫过程为马尔可夫链。

马尔可夫链的概念如下[5]：

随机序列Xn，在任一时刻n，它可以处在状态θ1，θ2，…，θN，且它在m＋k时刻所处的状态为qm＋k的概率，只与它在m时刻的状态qm有关，而与m时刻以前它所处状态无关，即有：

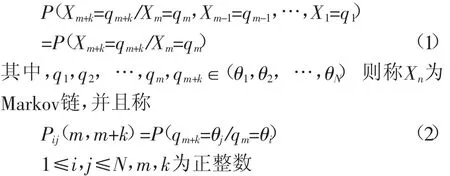
为k步转移概率，当Pij（m，m＋k）与m无关时，称这个Markov链为齐次Markov链，此时Pij（m，m＋k）＝Pij（k）。特别的，当k＝1时，Pij（1）称为一步转移概率，简称为转移概率，记为aij，所有转移概率aij，1≤i，j≤N可以构成一个转移概率矩阵，即

可见，k步转移概率矩阵P（k）与一步转移概率矩阵P之间的关系为P（k）=Pk。

完全描述一个马尔可夫链，除转移概率矩阵外，还必须引进一个初始状态概率矢量S＝（s1，…，sN），其中N为状态数。K个阶段后的状态向量可以由切普曼——格尔莫各洛夫方程得到：

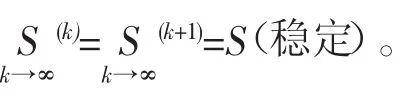
2 教学效果评价的马尔可夫模型建立

2.1 传统的教学效果评价模型的建立

教学过程是一个随机过程，因此可以用马尔可夫链的方法对教师教学效果做出评价，并在假设教学水平不变的前提下预测其将来的教学效果。

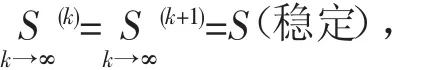
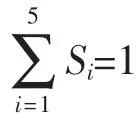
2.2 基于进步矩与进步度的教学效果评价分析

在上述讨论过程中，我们要想得知一位教师的教学效果，首先应从其以往教学成绩中得出转移概率矩阵，然后解其特征方程，这是一个相对复杂的过程，为此，我们引入进步矩与进步度的概念，以更简洁有效地对教学效果进行评价。

假设我们得到的某教师的转移概率矩阵为

学生成绩的优、良、中、合格、不及格五个等级，可以看到a12为本次考试为优的学生中下次转为良的概率，其它各元素意义类似。仔细分析此概率矩阵可以得到以下结论：

（1）主对角线上各元素代表在两次考试中等级没有发生变化的概率；

（2）下三角元素代表本次考试成绩变为更好等次的概率；

（3）上三角元素代表本次考试成绩变为更差等次的概率。

利用以上规律，我们给出以下概念：

进步矩（r）：转移概率矩阵中元素下标的差值，定义为r=i-j；它表示在两次考试中，成绩等级的差值，如元素a31的进步矩为2，a13的进步矩为－2。

3 实例分析

3.1 用传统方法建立马尔可夫教学模型并进行评价

以某校两位教师所带甲、乙两个班的成绩为依据，在两次考试中甲、乙两班的成绩转移情况如表1和表2所示。

表1 甲班成绩转移情况表

表2 乙班成绩转移情况表

甲班中上次成绩为优的14名同学中，分别有12名、1名、1名、0名、0名在本次成绩中转变为优、良、中、及格与不及格，其余数据意义类似。

由此，我们可以得到两个班的转移概率矩阵分别为：

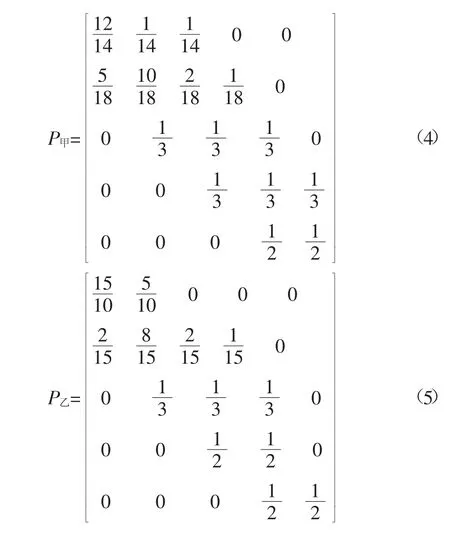
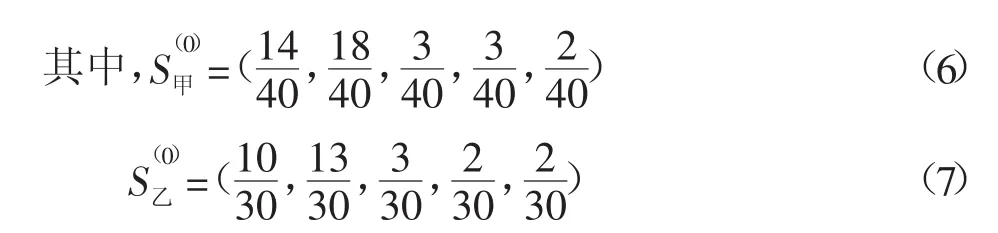
假设在教师的教学水平不变的前提下，我们通过解方程组SP＝S，即可以得出平衡时的等级分布。对甲班，有

解得平衡状态下甲班的成绩等级分布向量为

同理，可解得平衡状态下乙班的成绩等级分布向量为

3.2 基于进步矩与进步度的评价结果

根据前面所给出的定义，甲乙两矩阵的进步度分别为：

3.3 结果分析

由以上分析可见，利用马尔可夫过程理论对教学效果进行评价，不需要大量的历史数据，不需要考虑学生在某次考试中的波动性和随机性，计算简单且效果直观，既可以对教师的教学效果做出短期预测，也可以做出长期预测，这是该理论在应用中优越性的最明显的体现。

通过举例，我们分别求出了甲乙两班在稳定状态下的成绩等级分布情况，两个班的成绩质数相同，即经过足够长时间的教学之后，两个班的平均成绩趋于相同，这样似乎无法区别两位教师的教学效果。而本文的创新之处在于提出了进步度的概念，虽然两班平衡状态下的平均成绩相同，但是乙班的进步度略大于甲班。

进步度概念的提出，使我们在评价教学效果时不仅要考虑总体平均成绩，更要考虑学生在成绩等级间的变化情况，使评价依据更充分，更客观。

值得注意的是，我们在建立转移概率矩阵时所用到的两次成绩，并不是指具体两次考试中的成绩，而是指“两个”成绩，其中的每个成绩可以是一个阶段的成绩的均值，也可以是其统计分析的结果，这样可以克服数据选取上的偶然性对分析结果的影响，使评价更加客观真实。

4 结论

本文提出了一种基于马尔可夫过程评价教学效果的新方法，给出了成绩质数、进步矩与进步度的概念，克服了传统评价方法的缺点，对于更好地评价教学效果有很好的指导意义和实用价值。

［1］赵德龙，郑家恒.教学效果的齐次马尔可夫链分析软件开发研究［J］.山西大学学报，1994，17（1）：30-34.

［2］葛正洪.教学质量的时齐马尔可夫链评价法［J］.数理统计与管理，1996（1）：30-37.

［3］高娃.教学质量的马尔可夫链评估法［J］.内蒙古财经学院学报，2003，1（3）：82-83.

［4］杨欢.教学质量的马尔可夫链评估法［J］.重庆文理学院学报（自然科学版），2008，27（3）：22-25.

［5］谢锦辉.隐Markov模型（HMM）及其在语音处理中的应用［M］.武汉：华中理工大学出版社，1995.