基于动态逆的无人机机动控制律设计

初 阳，陈培龙

（中国船舶重工集团公司江苏自动化研究所，江苏 连云港 222006）

随着导弹、火炮、雷达等现代防空武器装备的日益完善，无人机的生存力受到更多越来越严重的威胁，例如来自地面火炮系统、地空导弹、空空导弹等武器的威胁。在战场上，可以通过提高无人机本身的机动性来规避地面或空中武器攻击以及空中危险区域障碍，提高生存概率。因此，研究无人机的机动控制律具有重要意义。

本文参照了非线性动态逆控制在战斗机上成功应用的先例上，将动态逆控制技术应用于无人机的控制律设计，分析前视雷达获得的目标障碍信息，设计适当的控制律，对无人机的航迹状态信息进行反馈控制，并加入PID控制来弥补系统误差，实现基于目标跟踪的无人机机动飞行控制[1]，使无人机能够完成小范围快速爬升和俯冲、大角度加速转弯等机动动作。

1 控制策略

本文中的无人机机动飞行控制结构是在姿态角稳定回路的基础上，加入一个机动指令产生器构成的。控制无人机做预期机动动作的机动控制策略如图1所示。在无线电上、下行信道畅通的条件下，由地面操纵控制计算机利用无线电定位系统实时提供无人机相对地面站的斜距、方位以及障碍物的位置、速度、加速度等信息，然后由机动产生器对这些信息进行处理，并输出机动指令控制量，通过无线电遥控信道把控制量发送到机体上，然后由机上执行机构控制无人机对这些指令进行跟踪，使无人机做出预期的机动动作[2-3]。

实现上述控制策略的关键在于控制器对机动产生器输出的机动指令跟踪。近年来动态逆技术成功通过有人机实际飞行测试，获得广泛认同，本文把这种高度非线性的动态逆技术运用到无人机上，以增强无人机的指令跟踪效果。为了进一步改善系统的稳定性，本文还对动态逆控制器的每个回路加入适当 PID控制，通过动态逆和PID的联合控制实现机动指令跟踪。

图1 无人机机动飞行控制结构

2 机动产生器

2.1 γF的解算

机动产生器的任务是根据当前传感器发出的位置和姿态信息，分析无人机下一步的机动动作，并解算出合适的航迹角，把期望的航迹角以指令的形式发送给控制器，通过控制器的实时反馈控制来实现无人机做出期望机动动作。

机动产生器一般安置在地面控制站上，当无人机飞行时，地面控制站根据机载雷达显示及当时的飞行状态判断如何规避障碍物，生成机动动作指令，然后通过无线电遥控信道将控制量发送到无人机上，由无人机上的执行机构控制机体作规避障碍的机动飞行。

本文所提出的机动控制算法是一种实时的导引控制方案，关键点在于如何根据当前的危险信息生成机动动作指令[4]。

图2中所示为雷达或机载传感器获取的当前无人机和障碍物A点的位置信息，经过机动产生器的处理，解算实时航迹倾斜角γF。

图2 爬升示意图

假设当前无人机坐标为(x,z)，障碍物 A点坐标为( xA, zA)，地面站的遥控机动点为 M ( x0,z0)，危险门限为H，则当前期望航迹倾斜角γF为

2.2 限制函数

为了使无人机遇到障碍物时不会立即产生过大的跃升角，且让机体在接近障碍物时充分利用其机动能力及时跃升，我们引入限制函数Lγ。并在此基础上引入角增益Kγ，通过对Kγ的调节，进一步提高无人机的机动能力。当前期望航迹倾斜角γF表达式如下：

地面限制函数Lγ的选取应考虑飞行速度V、当前航迹倾斜角γF、遥控距离R以及最大正负法向过载nmax和nmin。

为了保证安全，飞行速度V、最大法向过载也应对Lγ有所影响。角增益Kγ的主要作用是充分发挥无人机的飞行机动能力，使无人机机体能够尽快的跃升。一般来说，Kγ只取决于当前的航迹倾斜角γF。

3 控制器设计

整个无人机控制器由动态逆控制器和PID控制器两部分组成。

3.1 动态逆控制

非线性动态逆控制的原理是用非线性逆和非线性函数对消被控对象的非线性，从而构成了全局线性化；然后，在伪线性系统的基础上，通过相应的反馈及其增益，实现所需的系统响应。

无人机的非线性数学方程可写成如下的仿射非线性形式：

式中x为无人机飞行状态量；u为控制量；y为输出。

文献[5]已经证明系统可逆的充分必要条件为a(∑)≤ n ，其中a(∑)为相对阶数，并且当 a (∑)＝ n时系统完全可逆，当 a (∑)＜ n 时系统部分可逆。对于无人机非线性数学方程而言， a (∑)＜ n，所以，可以对无人机非线性系统方程进行部分线性化，系统存在部分逆。

利用时间多重尺度摄动理论，结合动态逆方法设计完全状态无人机非线性控制器。

根据 Azam M.和 Singh S.N.(1994)[6]以及 Kato O.和 Sugiura I.(1922)[7]对动态逆的研究，依照无人机的运动规律，将状态变量分成内回路变量(p,q,r)、外回路变量(φ,θ,β)和位置回路变量(V,α,ψ)，把非线性方程组分解为三个不同时间标尺的子系统回路。

式（3）对应于内回路， x ＝ ( p,q,r )T，u ＝(δe,δa,δr)T；对应于外回路， x ＝(φ,θ,β)T，u ＝ ( p,q,r )T；对应于位置导航回路， x ＝ ( V,α,ψ)T，u＝(φ,θ,β)T。

其中，p,q,r分别为三轴角速度； δe, δa,δr分别为升降舵、副翼和方向舵；φ,θ,β分别为滚转角、俯仰角和侧滑角；V,α,ψ分别为空速、仰角和偏航角。

用逆系统方法分别对各子系统求取部分逆，即

各回路组成的控制流程如图3所示[8]。

图3 动态逆控制回路

3.2 内回路动态逆控制律

求解六自由度无人机绕质心转动动力学方程，可以得到内回路控制律如下：

其中，

其中，b为翼展，c为平均气动弦长，S为翼面面积，ρ为空气密度。

在工程中，频带相差5倍便可进行时标分离，即在对内回路子系统(p,q,r)求系统动态逆时，变量(φ,θ,β)和 (V ,α,ψ)近似为常数。同理，在对外回路子系统(φ,θ,β)求系统动态逆时，变量(V,α,ψ)近似为常数。

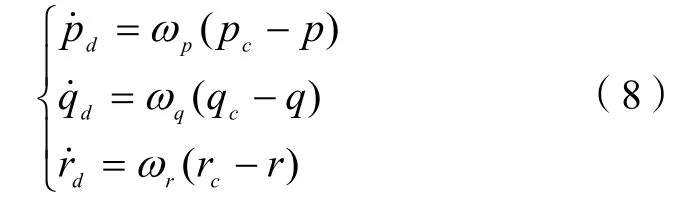
当舵面变化时，最先发生变化的是无人机的角速率(p,q,r)，其次才是姿态角。显然(p,q,r)为变化时间最短的变量，它对无人机的短周期运动起着重要作用，因此可以假设内回路带宽 ωp＝ωq＝ωr＝ 1 0rad/s 。

3.3 外回路动态逆控制律

对无人机绕质心转动运动学方程求逆，得出的外回路控制律如下。

其中，

(φ,θ,β)反映无人机的姿态角，它决定无人机的水平加速度，从而也确定了无人机的轨迹，假设外回路带宽 ωφ＝ωθ＝ωβ＝ 2 rad/s。

3.4 位置导航回路控制律

飞机轨迹运动响应慢，可以忽略角运动和角速率运动响应，从而使刚体运动方程简化为质点运动方程，并令β＝0，则数学模型可简化为：

用解析法和牛顿迭代法联合求解上述非线性方程组，可得

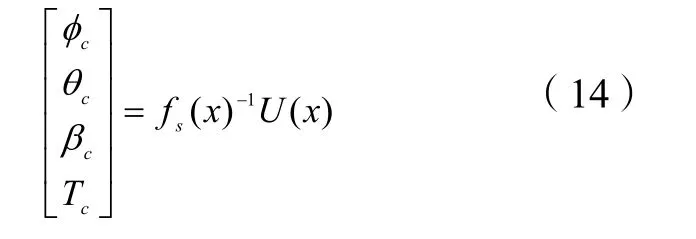
其中，

由于 (V ,α,ψ)是用来描述机体质心相对于地轴系的速度矢量的，设回路带宽为ωV＝ωα＝ωψ＝ 0 .4rad/s。

导航回路中，逆误差的存在会直接影响内回路变量，但只要控制器设计恰当，完全可以在内回路变量影响其余变量之前使误差收敛。

3.5 PID控制器

基于上述基本物理思想，对内回路采用智能控制的方法予以补偿，而其他回路则采用常规的PID控制来弥补因求近似逆而产生的误差。PID与动态逆控制律的结合，能更好的弥补各自的不足。

PID控制用以优化动态逆控制器的输入输出，其具体形式如图4所示。

图4 动态逆控制中的PID控制器

其中，xcmd和xc分别为动态逆回路中的输出和期望输入。

以某无人机为研究对象，选取飞行高度500m，飞行速度25m/s，重量15kg进行配平，在平衡点用小扰动法得到线性化后的纵向运动模型。

用根轨迹法结合Matlab中SISO工具箱对PID控制器进行参数设计，主要调节Ki和Kp的大小，使每个PID控制器都满足系统响应要求。

输入俯仰角指令为5°，在相同的条件下对PID控制与动态逆控制进行仿真，指令跟踪曲线如图5所示。

图5 两种控制方式跟踪响应对比

两种控制方式对输入的时域响应指标如表 1所示。

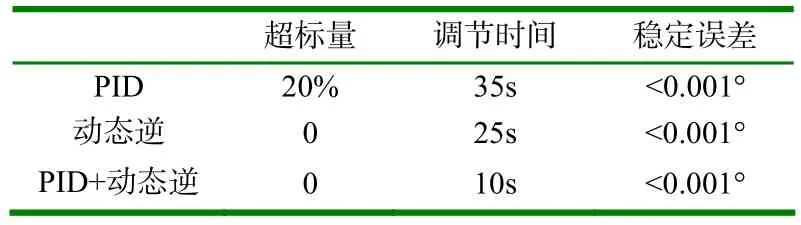
表1 两种控制器比较

从表1中可以看出，动态逆控制在指令跟踪方面明显优于PID控制，而且PID控制能在一定程度上弥补动态逆控制的不足。

4 Matlab/Simulink仿真

以Aerosonde无人机为例，在统一条件下进行仿真验证，具体仿真方法参照文献[9]。

1）机动指令生成算法仿真 假设无人机机动位置为 A ( 0,500)，危险区域为 B ( 32,510)，危险门限为50m，按照机动产生器中的机动算法生成的纵向机动指令曲线如图6所示。

图6 机动指令曲线

2）俯仰角跟踪仿真 对非线性机动航迹跟踪问题进 行 仿真 ，初 始 条 件 为 ： θg＝αg＝ψg＝5°，，希望飞机在某一时刻跟踪下列航迹指令：θ＝ θgsin(πt /15)， ψ ＝ ψgsin(πt /30)，仿真时间为40s。

图7为无人机速度分别是28m/s、20m/s和35m/s时的指令跟踪响应仿真曲线。

图7 动态逆俯仰角跟踪响应

在相同条件下，无人机以28m/s的速度定直平飞，仿真30s时刻时转入上述的航迹控制指令，并输入爬升角指令 γ ＝ 5°。

图8为当前无人机的航迹响应仿真曲线，螺旋线半径为 140m，爬升时平均空速为 28m/s，爬升高度150m。

图8 三维航迹跟踪曲线

3）误差补偿及横风影响仿真 加入横风影响，并在相同情况下仿真无补偿的动态逆控制器和有PID补偿的动态逆控制器的响应，进行对比。

图9和图10分别是1m/s和2m/s横风下俯仰角的响应情况。

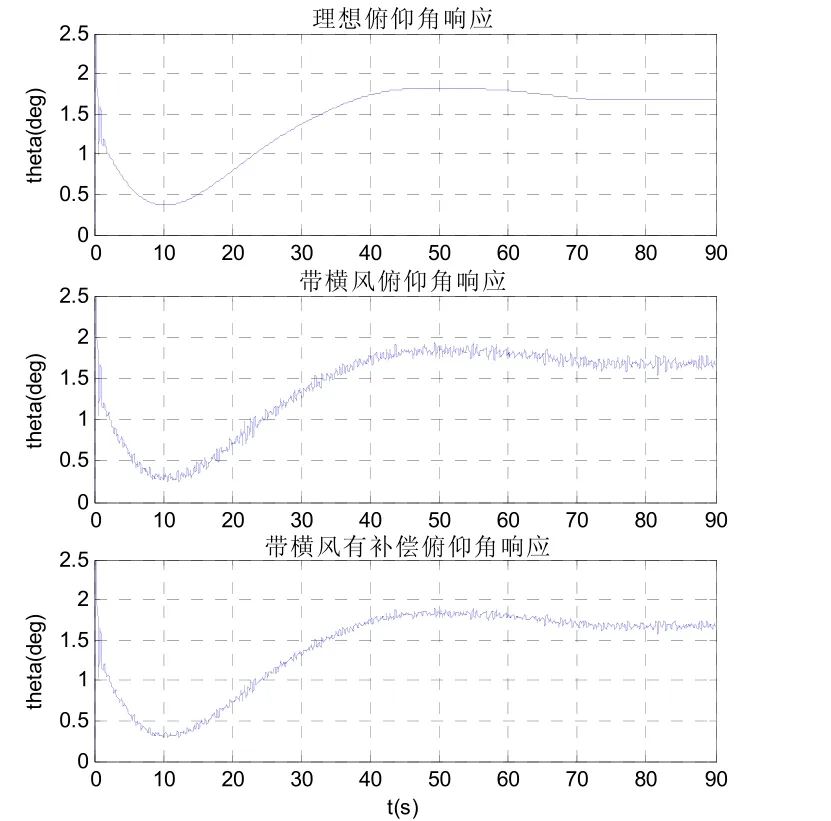
图9 横风1m/s俯仰角响应对比

图10 横风2m/s俯仰角响应对比

5 结论

仿真（1）中经过指令生成器生成的指令曲线爬升高度为 80m，高于危险门限（50m），证明本文所用的机动指令生成算法是有效的；仿真（2）可以看出，动态逆跟踪非线性机动航迹指令，响应速度快，较之其他的控制方式优越性较大。由于仿真指令采用的是螺旋线机动航迹，具有较强的代表性，因此本文所提出的机动控制器的设计是成功的。但同时也发现，例机只能在140m范围外做出稳定的机动航迹指令跟踪。而通过仿真（3）中的比对，可以看出有 PID补偿的动态逆控制器能够在很大程度上减弱横风对无人机的影响，提高基于动态逆控制器的无人机的稳定性。

仿真发现，应用本文的机动控制方案做小范围内的飞行机动时，飞行稳定性较差，究其原因主要在于制导与控制系统是分开设计的，这种设计在模型层次上制约了无人机的机动性。因此，将制导与控制系统统一建模同时设计是未来的一种改进方向。

[1]朱宝鎏. 无人飞机空气动力学[M].北京:航空工业出版社,2006.

[2]张明廉. 飞行控制系统[M].北京:国防工业出版社,1984.

[3]范志强,方振平. 超机动飞机的飞行控制研究[J].北京航空航天大学学报,2000(4):404 -407.

[4]包一鸣,姜智超,等. 一种实现大角度打击的制导律设计[J].北京航空航天大学学报,2008,34(12):1375-1378.

[5]李春文,冯元琨. 多变量非线性控制的逆系统方法[M].北京:清华大学出版社,1991.

[6]Azam M. and Singh S.N. Invariability and Trajectory Control for Nonlinear Maneuvers of Aircraft[J]. Journal of Guidance, Control, and Dynamics,1994,17(1).

[7]Kato O.and Sugiura I.,Nonlinear Inversion Flight Control for a Supermaneuverable Aircraft[J].Journal of Guidance,Control, and Dynamics,1992,15(4).

[8]朱恩,郭锁风,陈传德. 超机动飞机的非线性动态逆控制[J].航空学报,1998,119(1).

[9]王永林. Matlab/Simulink环境下无人机全过程飞行仿真技术研究[D].南京航空航天大学,2006.