基于Simulink的无动力自导深弹导引弹道仿真研究

任 磊，贾 跃，姜选凯

（海军大连舰艇学院，辽宁 大连 116018）

潜艇以其良好的隐身性和攻击能力被称为“水下杀手”[1]。随着现代潜艇机动性能和防护水平的不断提高，传统深弹依靠定时、触发引信攻潜已显得力所不及，而反潜鱼雷的使用又受到水深的限制，因此，在当前主要国家海军大国将战略核心从“蓝水”走向“绿水”的军事局势下，航空自导深弹依靠其自导性能和受水文条件限制小的特点逐渐成为反潜舞台上的重要角色[2]。无动力航空自导深弹便是其中一员。

无动力自导深弹的导引弹道描述起来比较复杂，但运用Simulink仿真可使问题描述简单化。Simulink是动态系统仿真的一个集成环境，可实现可视化建模。用户通过简单的鼠标操作就可建立起直观的系统模型，并且可以通过改变模块参数，实时观察系统行为的变化，从而摆脱了深奥数学推演的压力和繁琐编程的困扰，更重要的是，Simulink与虚拟现实工具箱配合能够进行更为直观的弹道视景仿真[3]。

1 自导深弹动力学模型[4]

自导深弹动力学模型可用矩阵形式表示，如式 1所示：

CEB为地面坐标系到弹体坐标系的坐标转换矩阵，

式中，M为深弹质量，（XC，YC，ZC）为深弹质心至浮心的矢径在弹体坐标系中三个轴上的分量；(x y z)为深弹位置坐标。(V x V y V z)，(ω x ω y ω z)为深弹速度、角速度在弹体坐标系三个轴上的分量；(φ θ )φ为深弹姿态角；（fs fgmsmg）分别为深弹在弹体坐标系所受定常运动的流体动力、负浮力、定常运动的流体动力矩、重力矩；m11，m22，m26，m33，m44，m55，m66，m35为有量纲附加质量。

2 目标潜艇运动的数学模型

潜艇运动数学模型可用式（2）表示,其中变量含义与深弹动力学模型中相同名称变量类同。因为潜艇在短时间改变深度比较困难，故仿真中假设潜艇运动在某一深度的水平面内，并且速度大小不变。

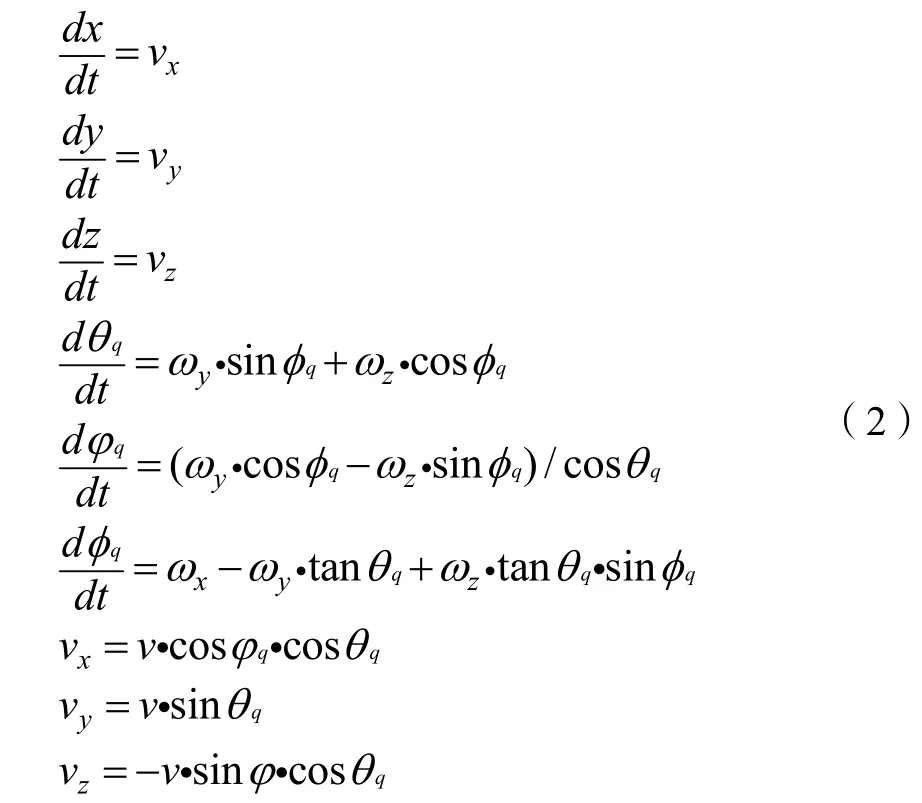
其中，（vx，vy，vz）为潜艇速度，（φq，θq，φq）为潜艇姿态角。

3 自导深弹的导引方式[5]

自导深弹采用声自导，依靠装在深弹头部的声自导系统测量目标相对深弹的位置，将所测得的信息经过一系列处理后变成操舵指令，操纵深弹自动导向目标。这里以尾追式自导方式为例进行研究。

深弹水下运动为六自由度的空间变换，包括深弹的位移和姿态。为研究方便，将其运动投影到两个相互垂直的铅垂面内分别研究，然后将这两个平面内的运动合成。其中一个铅垂面内深弹和目标的相对运动关系可以用图1表示。

图1 铅垂面内深弹与目标的相对运动关系

图1中，t为深弹位置，m为目标位置；tm为视线；r为深弹与目标之间的距离；q表示视线与攻击平面内某一基准线x0的夹角即舷角，从视线逆时针转向某一基准线为正；vt和vm分别是深弹和目标的速度；tη和mη分别是深弹和目标速度向量与视线的夹角即提前角，从速度向量逆时针转向某一基准线为正；Ψt和Ψm分别是深弹和目标的弹道偏角。当深弹自导声纳探测到在该平面内目标投影偏离基准轴左或右时，将此信息经过一定处理变成操舵指令并送到舵机装置，使其向右或向左打舵，从而使深弹不断接近目标。

4 深弹水下导引弹道仿真模型

运用Simulink建立深弹导引弹道的仿真模型，将导引弹道的各个环节模块化[6]。

4.1 深弹水下运动仿真模块

该模块是整个仿真模型的核心，其功能是利用Matlab的s函数解算深弹动力学模型求得深弹的运动学参数，该模块有两个输入，即深弹的水平舵角和垂直舵角，输出有12个，分别是深弹速度和角速度在弹体坐标系的三个坐标轴方向上的分量、深弹的俯仰角、偏航角、横滚角，以及深弹的位置坐标。

4.2 目标运动仿真模块

该模块功能是解算目标位置和姿态参数。输入为水平角速度，若潜艇为直航则输入为0；输出有9个，即潜艇的位置，三个方向上的速度和姿态角。其目标运动仿真模块如图2所示。

图2 目标运动仿真模块

4.3 制导与控制仿真模块

该模块的功能是根据自导深弹的导引方式，分别计算出深弹和目标在相互垂直的两个纵平面内投影的视线角和运动方向，根据两者之差和操舵规律分别得到垂直舵和水平舵的信号。

4.4 可视化模块

该模块的功能是将深弹攻击潜艇的水下弹道用三维动画形式直观显示出来，限于篇幅，这里不作讨论。

4.5 水下导引弹道仿真模型

将以上主要模块组合在一起，再添加一些用于控制仿真进程和显示仿真结果的示波器等模块，就构成了如图3所示的深弹水下导引弹道仿真模型。

5 仿真过程与结果分析

5.1 仿真研究对象

仿真针对影响深弹命中概率的因素展开研究。这里所说的命中概率与发现即命中的判据不同，而是深弹发现并能成功追上目标潜艇的概率。这与深弹水下的机动能力和探测能力密切相关，即与深弹的水下动力学特性和自导装置的性能有关。因此对于该命中问题，采用积分的解析方法无法解算，需要通过蒙特卡洛法进行统计试验才能解决。

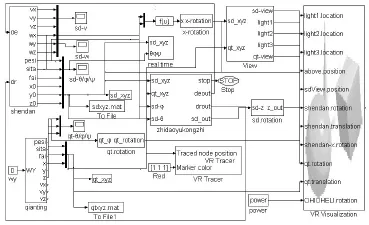
图3 水下导引弹道的Simulink仿真模型

5.2 仿真初始条件

仿真需要确定初始条件，即深弹水下运动仿真模块的12个输出变量和目标运动仿真模块的9个输出变量的初始值。为研究问题方便和不失一般性，文中所做仿真均为深弹入水并在垂直方向上达到稳态后，再开始搜索捕捉目标。

对于深弹而言，其俯仰角为-90°，深弹速度在弹体坐标系x轴上的分量为极限下沉速度，其余各初始值均取 0。在不给出操舵指令的情况下，根据深弹入水速度仿真可以得到其极限下沉速度为Vjx。其达到极限下沉速度的深度为hk。由于受空泡和速度影响，深弹入水后自导装置不能马上开始工作，故假设深弹自导装置入水垂直下沉至深度hk后开机。

图4 深弹水下攻潜误差散布示意图

对于潜艇的初始条件需要通过合理的分析和假设得出。如图4所示，在确定投弹时机时，为了能让深弹捕捉目标的概率最大，期望深弹在不打舵的情况下，垂直下沉至一定深度后其T点能与目标相遇，将此时深弹所处位置N称为期望相遇点，深弹从入水下沉至N点的时间称为理论发现时间。以T点为坐标原点，以潜艇航向的反方向为x轴，在水平面内建立坐标系。因为深弹入水时潜艇位置服从二维正态分布，其散布椭圆即为深弹和潜艇的综合误差散布椭圆，这里假设散布均方差为 σx＝80、σz＝10，潜艇期望航向为180º，航速为Vq，则深弹入水时潜艇散布椭圆中心坐标（ MxMz）可由潜艇航向，航速和理论发现时间按式（3）计算得出：

其中，s为自导作用距离，θ为自导作用扇面角，h为目标的深度，并假设潜艇航向、航速误差服从正态分布，均方差分别为3°和0.3m/s。

采用统计试验法和以上建立的仿真模型对深弹的命中概率进行仿真计算，图5为仿真流程图。其中，d为潜艇和深弹的直线距离，n为命中目标的次数，并假设有效毁伤半径为7m。

所建仿真模型及其初始条件的确定符合实际情况，即考察了入水前各种误差导致位置散布所影响的发现概率，又考察了深弹对目标的搜索和追踪概率。

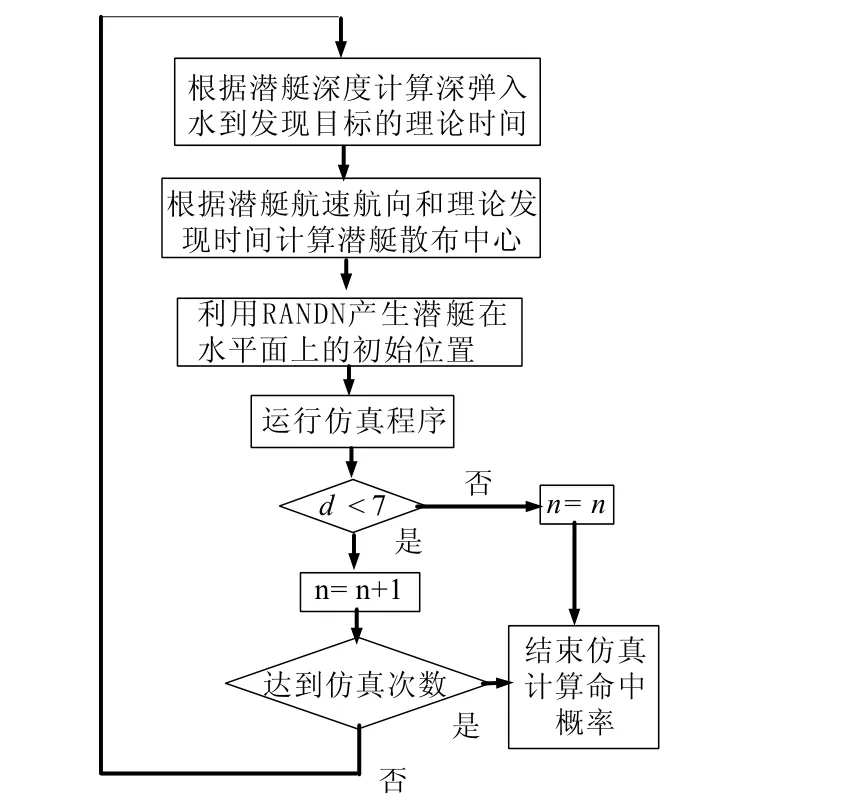
图5 仿真流程图

5.3 深弹偏转角度与舵角关系

由于深弹只依靠重力作用下沉，当其以某一固定舵角运动时，深弹在垂直方向上偏转至某一角度，达到平衡状态后开始匀速直线运动，此时深弹水平运动距离与下沉深度成正比关系，其比例系数为偏转角度的正切函数，而偏转角度又和舵角密切相关，所以舵角成为影响深弹机动范围的重要因素之一。这里只给出打单舵情况下深弹的偏转角度，双舵偏转研究方法类似且结果相差不大。

由图6可以看出，舵角增大，偏转角度增大，但舵角越大，偏转角度变化的幅度越小，并且当舵角超过0.12后，偏转角度无法再增大，从仿真的可视化结果中可以看到，深弹偏转角度大于0.12时，深弹失去稳态。

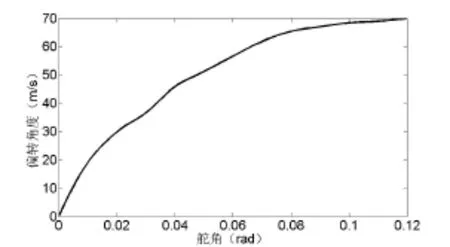
图6 偏转角度与舵角的关系

5.4 深弹速度与舵角的关系

深弹的偏转角度决定了深弹的机动范围，而对于采用尾追自导方式的深弹而言，能否成功追上目标还取决于深弹的追踪能力，即深弹的速度。而深弹的偏转角度不同，其速度也就不同，当深弹以固定舵角运动达到平衡状态后，其运动速度也不变。由此可见最终对深弹速度起重要影响的还是舵角。

图7是深弹速度和舵角的关系。这里也只给出打单舵情况下深弹的偏转角度，双舵偏转研究方法类似且结果相差不大。由图7可以看出，舵角增大，深弹的运动速度越小，并且舵角越大，这种影响越为显著。

5.5 目标深度对命中概率的影响

假设目标潜艇速度为 8kn，深弹自导作用距离为300m，自导作用扇面角为140 º，仿真次数为500次，经插值后得到目标深度对命中概率的影响如图 8所示。

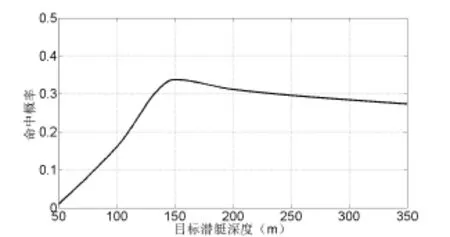
图8 目标潜艇深度对命中概率的影响

由图8可见，深弹对目标潜艇的命中概率随着潜艇深度的增加先增加后减小，因为命中概率开始主要是受自导扇面角的影响，从深弹下沉过程中的整个自导作用区域看，开始自导作用区域是一个圆锥体，随着深度增加，水平作用范围扩大，命中概率也增大，当到达一定深度后自导作用区域为圆柱体，水平作用范围不变，此后命中概率主要受潜艇位置散布误差的影响，因为深度越深，理论发现时间越长，潜艇航向航速误差引起的位置误差就越大，所以命中概率逐渐减小。

5.6 自导作用距离对命中概率的影响

假设目标潜艇深度为150m，速度为8kn，深弹自导作用扇面角为140º，仿真次数为500次，经插值后得到自导作用距离对命中概率的影响如图9所示。

图9 自导作用距离对命中概率的影响

由图9可见，随着自导作用距离增加，命中概率增大，但增大到一定值后其增大的幅度逐渐减小。这是因为自导作用距离增加增大了深弹搜索范围，有利于深弹更早发现目标，但当自导作用距离超过目标深度与自导扇面角半角正割的乘积后，即使再增加，其在目标深度的水平搜索范围也不会变化，所以自导作用距离再增加，命中概率基本不变。

5.7 自导作用扇面角对命中概率的影响

假设目标潜艇深度为150m，速度为8kn，自导作用距离为300m，仿真次数为500次，经插值后得到自导作用扇面角对命中概率的影响如图10所示。

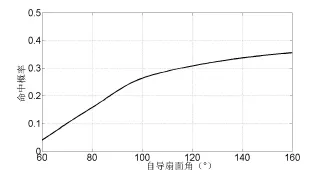
图10 自导作用扇面角对命中概率的影响

由图10可见，随着自导扇面角增加，命中概率增大，当自导扇面超过140º后，命中概率基本不增加，因为深弹最大的偏转角度为69.1º，即使深弹自导作用扇面再增大，对命中概率的影响也很小，所以仅仅增大自导装置的扇面角意义不大。

5.8 目标运动速度对命中概率的影响

假设目标潜艇深度为150m，深弹自导作用距离为300m，自导作用扇面角为140º，仿真次数为500次，经插值后得到目标速度对命中概率的影响如图 11所示。

图11 目标潜艇速度对命中概率的影响

由图11可见，目标速度对命中概率的影响相当显著，目标速度越大，命中概率越小，可见无动力深弹速度上所受到的限制是其追踪能力欠缺的关键因素，为此在使用中应尽可能投放在目标潜艇的运动前方。

6 结束语

通过对以上仿真结果的分析可以总结归纳得出以下几点结论：

1）深弹命中概率与目标深度有关，随着潜艇深度的增加，命中概率先增大后减小，因此深弹浅水反潜比鱼雷更具优势，能够弥补鱼雷在工作深度上的盲区。

2）为提高武器研制的效费比，自导性能参数理论设计时应考虑到深弹机动性能及其浅水反潜的战术目的，其自导作用距离为其期望工作深度与自导扇面角半角正割的乘积；自导扇面角应略大于2倍极限偏转角度。

3）无动力自导深弹攻击低速航行的潜艇效果较好，并且投弹时应尽可能使深弹落在目标潜艇的运动前方。

此外，从仿真过程可以看到运用Simulink进行弹道仿真方便快捷，并为无动力自导深弹水下导引弹道的可视化仿真提供了更为直观的工具。

[1]姜选凯,赵学涛,贾跃. 航空自导深弹攻潜命中概率分析[J].火力与指挥控制,2009(8):64-67.

[2]孙明太. 航空反潜战术[M].北京:军事科学出版社,2003.

[3]黄永安,马路,刘慧. Matlab7.0/Simulink6.0建模仿真开发与高级工程应用[M].北京:清华大学出版社,2005.

[4]张宇文. 鱼雷弹道与弹道设计[M].西安:西北工业大学出版社,1999.

[5]严卫生. 鱼雷航行力学[M].西安:西北工业大学出版社,2005.

[6]赵军民,等. 基于MATLAB/Simulink的弹道仿真模块化设计[J].弹箭与制导学报,2007(1):147-153.