环境例行定性分析或快速筛选结果的可靠性

冷 庚，谢 晴，王 彬，杨嘉伟，但德忠

（四川大学建筑与环境学院，四川 成都 610065）

1 引 言

为了迅速获取环境中的可靠信息，例行分析中定性或快速筛选分析越来越广泛地被采用。这类方法能为突发性环境事故的快速处置、决策提供依据。在应急监测中，相对于获得准确的结果而言，人们对样品浓度是否超出相关标准限量更为重视。此外，定性或快速筛选分析还具有其他一些明显优势，如成本低廉、分析速度快、操作简单以及可将采样和分析过程中因时间耽搁产生的误差减至最小等。

对未知样品的测定，应首先进行定性与快速筛选分析。为了判断方法是否符合要求，首先必须了解分析方法的相关特征，如精密度、适应性、可靠性以及检出限等。对定量分析结果的可靠度，人们已进行了较广泛深入的研究。但是，对定性分析或快速筛选分析结果的可靠度却少有研究[1-4]。定性分析或快速筛选分析结果的可靠度不能用与定量分析一样的方式表达，即不能用表示分析结果离散度的一个参数来表示。相反，结果的可靠性本质上具有概率的性质，可以用犯错误的概率来表示。这些错误是随机的或是由误差造成的，是分析结果不可靠的来源。在分析过程中，必须充分考虑不可靠度以及做出误判的概率。

目前，有人研究了如何处理定性分析或快速筛选分析中结果的可靠性，但在应用方面尚未找到最好的方法[3]。该文介绍用于处理定性分析或快速筛选分析可靠度的一些方法，这些方法均基于概率计算。

2 定性分析中可靠度评估方法

目前，评估不可靠性的方法较多，如贝叶斯定理（Bayes’Theorem）[5]、列联表（Contingency Tables）[6]法、类似于定量分析中计算不确定度的统计间隔法以及性能曲线法。

2.1 列联表

列联表将定性分析视为分类问题。最简单的情况是将样品分析结果分为两种情况。例如，有毒化合物的浓度或是高于或是低于某一特定值。样品分析的结果可能为正（大于或等于某一特定值），也可能为负（小于某一特定值）。

针对快速筛选分析有两种结果并可能反映两种实际情况，可以建立2×2列联表。表的维度可从2×2到n×p，n和p表示类别的数量。例如，检测花生中是否含有黄曲霉素，标准允许的最大限量为2μg/g。筛选试验采用酶联免疫吸附试剂盒[7]。当黄曲霉素含量高于限量时，发生免疫反应，根据颜色变化判断结果。如果颜色变为白色（阳性），表明黄曲霉素的含量大于或等于2 μg/g；如果颜色变为蓝色（阴性），则黄曲霉素的含量小于2μg/g。试验300个样品，通过高效液相色谱分析，发现其中150个样品的含量大于或等于2μg/g。其余150个样品含量均低于限量值。测定结果的分布如表1所示。

表1 花生中黄曲霉素快速筛选分析的2×2列联表

从表1可知，样品中黄曲霉素的实际含量有“大于或等于”或“小于”两种情况，对应结果或为阳性（+），或为阴性（-），N为样本大小。黄曲霉素的分析结果有4种可能的情况：大于或等于2μg/g，分析结果为阳性，称为真阳性，tp=135；类似地，有真阴性，tn=129；假阴性，fn=15；假阳性，fp=21。利用列联表还可以评价分析方法的性能，如灵敏度、特异性、阳性预测值（PPV）及阴性预测值（NPV）。

表2 性能参数的计算表达式

表2中的式（1）可用于计算方法的灵敏度，该灵敏度用试验获得的真阳性结果数占实际阳性结果总数的比来表示。上例中，方法的灵敏度=（135/150）×100=90%，即分析黄曲霉素含量大于或等于2μg/g的100个试样时，其中90个试样的结果呈阳性，10个试样的结果呈阴性（假阴性）。然而，理想的分析方法测出的100个试样中黄曲霉素含量均应大于或等于2μg/g。检测灵敏度也称为方法的功效。在统计假设检验中，功效定义为1-β，β表示获得假阴性结果的概率[6]。

特异性定义为真阴性数占实际阴性总数的比例，即表2中的式（2）。上例中，方法的特异性=（129/150）×100=86%，即分析黄曲霉素含量低于2μg/g的100个试样时，其中86个试样的结果呈阴性，14个试样的结果呈阳性（假阳性）。而理想的分析方法测出的100个试样中黄曲霉素含量均应低于2 μg/g。在统计假设检验中，特异性与显著性水平α有关，α表示获得假阳性结果的概率。

根据不同的分析目的，比特异性更高的灵敏度可能更可取，反之亦然。值得注意的是，灵敏度的增加往往伴随着特异性的下降，而灵敏度和特异性均取决于样本大小N。即N越大，列联表中包含的信息越多，由此计算出的灵敏度和特异性的可靠性就越高。

阳性预测值表示试样结果呈阳性时，黄曲霉素的实际浓度大于或等于2μg/g的概率。PPV=（135/156）×100=86.5%，表明当有100个试样的结果呈阳性时，其中86个试样的含量将大于或等于2μg/g，而有14个试样的结果呈假阳性。类似地，阴性预测值表示真阴性结果占测出的阴性结果总数的比例。上例中，PNV=（129/144）×100=90%，意味着当有 100 个试样的结果呈阴性时，其中90个试样的含量将小于2μg/g，而有10个试样的结果呈假阴性。

列联表常用来估计快速筛选分析的可靠性，以及不同分析方法的比较。这种比较是基于不同筛选方法对相同样本的灵敏度和特异性而言。值得注意的是，不同方法灵敏度和特异性的差异可能是由偶然性造成的，因为实际情况与检测结果间的差异受随机误差的影响，当试样数量较小时更是如此。为了评估这些可能的差别，某些统计检验能从列联表中获得一些正确的结论[6]。

列联表用于生物检测（如免疫学检测）时，一些术语和定义与其在分析化学领域中的含义有所不同，如灵敏度和特异性。尽管列联表为试验方法的整体性能提供了概貌，但是它不能估算个别样本出现误差的概率，而且其性能很大程度上取决于样本的大小以及用于构建该表的试验设计。

2.2 贝叶斯法

在处理二分结构（如是/否、存在/不存在、成功/失败）时，贝叶斯法是一种用于表达和更新概率的老方法，在定性分析中已获得应用[5]。当考虑到历史和条件概率分布时，贝叶斯定理可对相似情况下采用类似测量的概率进行预测[8]。Ellison等[5]评述了贝叶斯定理在计算定性分析结果可靠性的应用，并认为贝叶斯定理在测量结果可靠度方面比列联表中的概率更适用。

仍以黄曲霉素为例，在检测结果呈阳性（p）的条件下，试样中黄曲霉素含量大于或等于规定限量值（a）的条件概率计算表达式为：

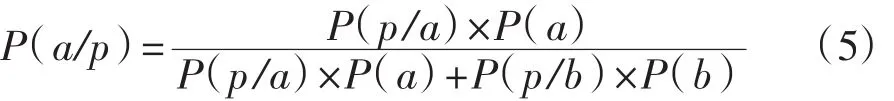
式中：a——黄曲霉素含量大于或等于2μg/g；

b——黄曲霉素含量小于2μg/g。

P（a）和 P（b）是各自的事前概率，表示预先不知道的情况下取得阳性结果p或阴性结果n的概率。先验概率往往是最难量化的参数。根据历史数据或经验可以对先验概率进行估计。当无法获得充足的试验数据，也无法证明黄曲霉素含量是高于还是低于规定限量值时，先验概率通常设为0.5。

P（p/a）表示黄曲霉素含量大于 2 μg/g时，检测结果呈阳性的概率，P（p/b）表示黄曲霉素含量低于2 μg/g时，检测结果呈阳性的概率。这两种概率分别与假阴性和假阳性的比例有关[9]。

准确地说，假阴性的概率应该是P（n/a），它与P（p/a）有关，即 P（p/a）=1－P（n/a），而 P（p/b）自身就是假阳性概率。Ellison等[5]认为，这些概率可通过诸如直接实验测定、根据已知或假定的阈值分布以及利用相关数据库或理论预测的方法来评价。第一种方法最简单，它包括向待分析任务提交尽可能多的特征材料，然后观察结果。对大小为N的样本，已知黄曲霉素含量均低于2μg/g，当检测结果有p个阳性时，则P（p/b）=p/N。类似地，已知黄曲霉素含量均大于 2 μg/g，当检测结果有 n 个阴性时，则 P（n/a）=n/N。同理，当试样中黄曲霉素含量均高于2μg/g时，结果呈阴性的条件概率可用与式（5）类似的式子计算，不同的只是把公式中的P换成为n。

当对先验概率一无所知时，P（a）和 P（b）都取0.5。如果测试结果与表1相同，利用贝叶斯定理计算的概率如下：

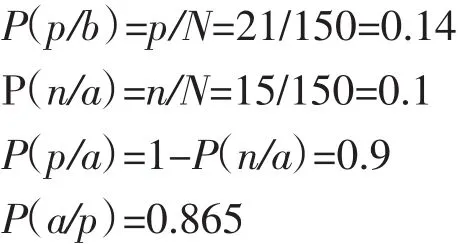
这意味着，当试样的检测结果呈阳性时，黄曲霉素含量高于2μg/g的概率为86.5%。用同样的方法，可计算出 P（a/n）=0.104。

从上述表达式，可以发现列联表和贝叶斯定理之间存在一定的关系，因为它们都是基于概率论。这种关系可通过似然比来建立，似然比是两个条件概率的比值，并且与列联表中灵敏度和特异性这两个参数有关，通过下式可以计算似然比：

应当指出，如果想用这种方法得到很好的估计值，则需要有大量的分析试样。从分析的角度来看，贝叶斯法的弊端在系统命名的复杂化以及难以量化不同概率项。与列联表相比，贝叶斯法不仅能对新试样的可靠性予以估计，还能通过先验概率将先前的信息统合到一起。

2.3 统计间隔

目前，Pulido等开发了一种用于计算定性分析结果可靠度的简单程序[10]，该程序与计算定量分析的不确定相似，都基于统计间隔，服从高斯正态分布，并已广泛用于计算检出限[11-12]。该程序能建立浓度的标准限量值和仪器响应信号间的联系，通过比较常规样品与标准限量值的响应，便可做出“是/否”的决定，其出错的概率是确定的。该法与前述方法的区别主要有两点：由于处理仪器响应信号，因此需要连续数据而非二进制数据；通过实验确定分析结果的可靠性，需制备标准限量浓度的分析样，而在前述方法中，需制备不同浓度的分析样。

当采用统计间隔时，以中等精度对一套独立制备的含有标准限量浓度待测物的试样分析nSL次，以求囊括造成结果不可靠的主要来源。这样，可以计算仪器响应的平均值及其标准偏差s。

为了比较某试样的仪器响应ri是否低于、等于或高于标准限量，需要确定阈值rcut-off。假设仪器响应服从正态分布，则通过平均值单侧的较高或较低预测界限计算rcut-off：

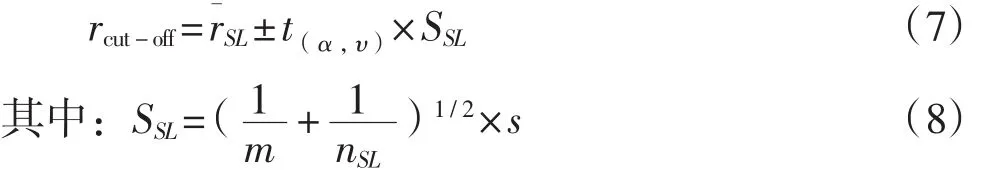
式中：t（α，υ）——显著性水平为 α、自由度为 υ 时单侧T统计值；

nSL——计算进行独立分析的次数；

m——试样重复分析的次数（通常m=1）；

s——校正样品仪器响应的标准偏差。

SSL和υ的值取决于建立的试验设计。在无试验设计的情况下，SSL可用式（8）来表示。式（7）中的“±”取决于标准限量以何种方式表述。

仍以黄曲霉素为例，欧盟（EU）相关法规规定其最大含量为2 μg/L。采用荧光快速扫描技术，分析含2 μg/L黄曲霉素B1的34个样品，结果如下：。当 α=5%时，根据式（7）和式（8）得。因此的任何样品在统计学上若等于或低于则满足法规规定。同理，的任何样品在统计学上若高于rSL，则认为不符合法规规定，该判断出错的概率为5%。

由式（7）可知，适应性取决于犯I型错误或假阳性的先验概率α。一旦分析人员取定一个α，那么阈值rcut-off可以帮助分析人员对某样品的适应性进行后验决策。即只有相应于测试样品的仪器响应ri被记录时，才能做出决定，通过这种方式，测量的可靠度就从分析结果转移到阈值，通过对ri和rcut-off的简单数字对比，便能做出适应/非适应的判断。这种方法适合日常的快速筛选分析。

筛选限rscreening也是在考虑到犯II型错误或假阴性的β概率下计算出来的[10，13]。仍以黄曲霉素为例，当试样中黄曲霉素浓度未超出标准限量CSL时，β是指试样符合限量要求，而实际却高于CSL的概率。为了用式（9）计算rscreening，分析人员必须固定3个参数α、β或rcreening-中的两个，后者是ri和间差异的最小预期值，分析人员希望用试验结果得到的α和β的概率对其进行计算（如图1所示）。

图1 定性分析中考虑了犯I型和II型错误的概率α和β时的标准信号、阈值信号以及筛选限

式中：Δ（α，β，υ）——自由度为nSL-1的非中心t分布的非中心参数，它取决于出错概率α和β。

根据式（9），可推断出筛选系统中的筛选限取决于犯I型和II型错误的概率、筛选方法的精度及实验结果，而实验结果又取决于标准和试样的重复测定次数。当试样的浓度低于标准限量时，也可通过相同的推理计算筛选限rscreening，只需将式（9）中的加号变为减号。

筛选限是筛选系统的先验值，一旦将其赋予浓度意义，它便可以用于不同方法的比较或解决某一具体问题方法的选择。当CSL=0时，筛选限就是检出限。

这种方法只适于处理能提供数值和连续响应的仪器筛选系统。通常，用于定量分析的仪器法适合作为筛选法。然而，当不能得到二分响应和二元响应时，这种方法不适用。

2.4 性能曲线

评估可靠性的另一种方法就是建立性能曲线[14]，它是通过采用快速筛选技术分析不同浓度的样品而建立的。通常，需制备不同浓度的标准的样品空白，使其最终浓度在标准限量值上下。以中等精度对每个浓度的试样进行多次重复测定，对每个浓度水平计算出阳性结果的数量，据此绘制浓度水平与阳性结果百分比曲线。该曲线可能确定阈值浓度，即对一定的误差概率，仪器响应的浓度高于标准限量值。此外，对一定的误差概率α和β，还可以计算出不可靠间隔或区间。

图2是用前述酶联免疫吸附试剂盒测定黄曲霉素B1的性能曲线。为此，需制备5个浓度的加标样品（2个高于标准限量，2个低于标准限量，1个等于2μg/g标准限量），每个浓度重复测定10次，结果见表3。分析完成后，计算阳性与阴性结果的百分数。根据图2中假阳性或假阴性出错的概率，可以确定阈值浓度，该浓度在图上可用一条垂线表示。根据出错概率的不同，该垂线可以左右移动。如果标准限量浓度（2μg/g）的样品可以接受，那么出错的可能性约是50%。在定性或快速筛选分析中，通常关心的是怎样获得低的假阴性概率。在这种情况下，阈值水平可设在1μg/g和1.5μg/g之间。例如，若将阈值浓度设为1.5μg/g（垂直线），那么有10%的结果呈假阳性，即可认为10个样品中有1个高于标准限量，而实际上却低于该限量。

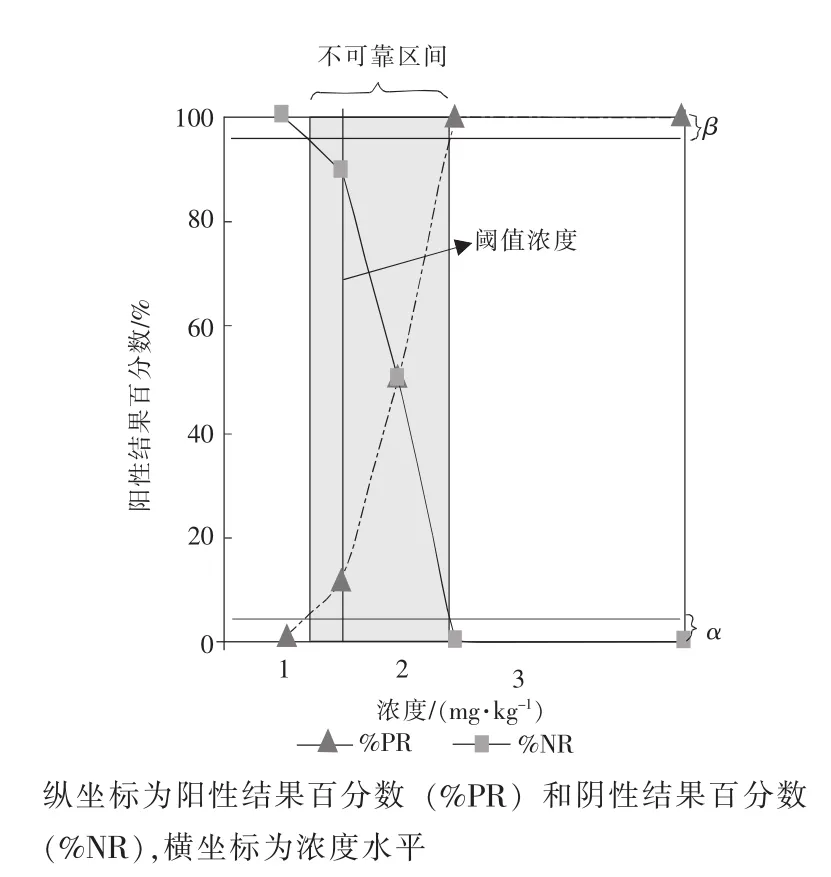
图2 性能曲线

表3 标准限量附近不同浓度的空白加标样品的分析结果

为了确定不可靠区间，假阴性和假阳性率都必须固定。在前例中，如果误差概率α和β都定为5%，那么不可靠区间在1.25μg/g和2.4μg/g之间。显然，性能曲线越准确，不可靠区间越窄。而这一点又与每个浓度重复分析的次数和浓度水平的数量有关。

与贝叶斯定理类似，该法的主要缺点是当位于可靠区间内浓度的样品重复测定次数较少时，在有限样本容量中获得阳性或阴性结果的概率也低。此外，考虑到成本和时间，增加重复次数会产生一些消极的后果。当对现行筛选方法的精度缺乏认识，或用试剂盒来分析样品时，这种方法是有用的，因为试剂盒的响应不是阳性就是阴性。当获得可疑结果时，性能曲线会发生变化。性能曲线适用范围广，适用于所有类型的快速筛选系统。

3 结束语

定性分析或快速筛选分析中结果的可靠性评估方法有四种，具体方法的选择主要取决于分析问题本身以及所用的快速筛选技术。利用上述方法来估计分析结果可靠性，实验所需的样品数量和浓度水平都是不同的。如果利用列联表估算可靠性，虽然试样只可能有两种情况，即高于或低于标准限量值，但分析不同浓度的样品仍是需要的。同样，当用性能曲线来处理数据可靠性，仍需分析不同浓度的样品，且每个浓度需重复测定。当用统计间隔来估算结果的可靠性时，只需分析某个浓度的多个样品。

[1]Valcárcel M，Cádenas S，Gallego M.Sample screening system in analytical chemistry[J].Trends in Analytical Chemistry，1999，18（11）：685-694.

[2]Barwick V J，Ellison S L R，Fairman B.Estimation of uncertainty in ICP-MS analysis：a practical methodology[J].Analytica Chemica Acta，1999，394（2-3）：281-291.

[3]Desimoni E，Mannino S，Brunetti B.On the assessment of compliance with legal limits： Part 1： Signal and concentration domains [J].Accreditation & Quality Assurance，2001，6（11）：452-458.

[4]Malissa H，Riepe W.Statistical evaluation of uncertainty for rapid tests with discretereadings-examination of wastes and soils[J].Accreditation&Quality Assurance，2000，5（12）：495-498.

[5]Ellison L R，Gregory S，Hardcastles W A.Analyst[M].Cambridge，UK，1998.

[6]Massart D L，Vandeginste B G，Buydens L M C，et al.Handbook of chemometrics and qualimetrics，Part A[M].Amsterdam，The Netherlands：Elsevier，1997.

[7]Rhone R B.Aflatoxins commercial test kit[EB/OL].http://www.r-biopharmrhone.com/pro/afla/afla.html.

[8]Mcfall R M，Treat T A.Quantifying the information value of clinical assessments with signal detection theory[J].Annual Review of Psychology，1999（50）：215-241.

[9]Currie L A，Horwitz W.Analyst[M].Cambridge，U.K，1994.

[10]Pulido A，Ruisánchez I，Boqué R，et al.Estimating the uncertainty of binary test results to assess their compliance with regulatory limits[J].Analytica Chimica Acta，2002，455（2）：267-275.

[11]Liteanu C，Rica I.Statistical theory and methodology of trace analysis[M].New York，USA：Ellis Horwood，1980.

[12]Currie L A.Nomenclature in evaluation of analytical methods including detection and quantification capabilities[J].Pure&Applied Chemistry，1995，67（10）：1699-1723.

[13]Aitken C G G，Stoney D A.The use of statistics in forensic science[M].Sussex，UK：Ellis Horwood，1991.

[14]Song R，Schlecht P C，Ashley K，et al.Field screening test methods：performance criteria and performance characteristics [J].Journal of Hazardous Materials，2001，83（1-2）：29-39.