大坝观测中测点处混凝土的应变重分布

陈灿明 黄卫兰 唐崇钊 张大伟

（1.南京水利科学研究院，江苏 南京 210029；2.水利部水科学与水工程重点实验室，江苏 南京 210029）

一、引 言

混凝土大坝观测埋设的应变计和无应力计，可以获得测点混凝土的非应力应变和应力应变；通过混凝土徐变试验提供的弹性模量E和徐变度C、或徐变系数φ可将应力应变转换为混凝土的观测应力。在这一转换计算中，为取得较为接近实际的结果，不但涉及到徐变测试的方法、计算参数的取值、转换计算的基本方程与方程形式，还应注意测点混凝土与周边混凝土变形特征的差异及与之相关的计算偏差。

大坝混凝土徐变测试常用试件主要为φ20cm×60cm的圆柱体，亦有φ15cm×45cm圆柱试件。因原级配混凝土含有粒径较大的粗骨料，成型时需将大于试件直径1/4～1/5的粗骨料剔除。用这种试件进行加载测试得到湿筛小试件混凝土弹性模量和徐变度（或徐变系数），记以Em、Cm(或φm)。计算混凝土的观测应力时，不宜直接采用Em、Cm(或φm)，还应采用经验取值法换算得到原级配混凝土的徐变特征参数E、C(或φ)。

用作应变观测的传感器有DI-25和DI-10两种型号应变计。埋设DI-25型应变计（或应变计组）时，在测点位置的一定范围需将大于8cm的骨料剔除；埋设DI-10型应变计时需剔除3cm以上的粗骨料。测点范围内混凝土与周边混凝土的弹性模量和徐变度（或徐变系数）存在的差异，可在一定范围内出现应力和变形的重新调整，用出现偏差的应变与原级配混凝土的徐变参数推算观测应力显然存在偏差。本文依据室内试验的有关结果讨论发生应变重分布的条件和数量变化。

二、室内试验湿筛混凝土与原级配混凝土徐变和弹性模量

大坝混凝土粗骨料粒径可达15cm，常规徐变试验需要将粒径大于4cm的骨料用湿筛法剔除。湿筛后二级配混凝土的灰浆率ηm将高于原级配混凝土的灰浆率η。因徐变主要取决于混凝土中的灰浆体，湿筛二级配混凝土的徐变度Cm也因灰浆率的提高而大于原级配混凝土的徐变度C。据国内外有关学者的试验结果，认为徐变变形与灰浆率基本成正比关系，可用下面的关系式表示

式中:C、η－原级配混凝土的徐变度和灰浆率；

Cm、ηm－湿筛后二级配混凝土的徐变度和灰浆率；

β－比例系数，与骨料级配、工艺等有关的试验常数。

国内早期（北京水科院）的试验结果为：混凝土原级配与湿筛后混凝土的灰浆率之比在0.62～0.87范围，比例系数β = 0.82～1.16，平均=0.98。美、日有关学者得到的试验结果为β=0.93～1.07。公式（1）可以用一个刚性模型和一个流变模型串联的组合体变形描述，这时假设流变体的变形与相对体积成正比。在统计意义上因比例系数β接近于1，在未作对比性测试的情况下，可用下面公式推算原级配混凝土的徐变

式中:λ－灰浆率比值或徐变度比值，λ=η/ηm。

二滩拱坝曾用尺寸φ45cm×90cm和φ20cm×60cm两种圆柱体试件进行徐变和弹性模量的对比测试，两种试件混凝土的徐变比C大/C小和弹模E大/E小列于表1。

经测试，四组结果的平均值为：β =1.03、φ大/φ小=0.70、E大/E小=1.04。据称中国水电科学研究院的结果为E大/E小=1.03～1.09，美国胡佛坝的结果为E大/E小=1.05～1.09。

表2列有溪洛渡水电站大体积混凝土的弹模与徐变测试结果相对值。徐变对比测试的试件尺寸为φ45cm×90cm和φ20cm×60cm，弹模对比测试的试件尺寸为φ45cm×90cm和φ15cm×30cm。该测试得到的徐变比系数β值接近于1，弹模比值E大/E小较前结果有较大提高。碾压混凝土试验得到的徐变比系数β也在1左右。

表1 二滩拱坝混凝土徐变和弹模对比测试结果

表2 溪洛度水电站大体积混凝土徐变和弹模对比测试结果

从国内几个大坝工程混凝土（常态混凝土和碾压混凝土）的试验结果看，原级配混凝土与湿筛后二级配试件混凝土的徐变比和弹性模量比之常见范围大致如下：

原级配混凝土与观测应变传感器埋设位置混凝土灰浆率比值λ应不小于0.70。

北京水科院惠荣炎等曾导出一个推算公式，由湿筛后混凝土的弹模测值Em、灰浆率比值λ=η/ηm和粗骨料弹模Eg推算原级配混凝土弹模E，公式如下

推导该公式时，设原级配混凝土试件的变形用两个弹性模型（Em和Eg）串联的变形描述，其单位变形与两个弹性模型单位变形的相对体积Vm/V、Vg/V成比例。该公式推算值与实际试验结果相差较大，说明原级配混凝土部分粗骨料筛除引起的弹性模量变化既有材料（Eg、Em、λ）和试验技术（试件形状尺寸、成型方向、振捣）因素，还有粗骨料表面的泌水弱层和材料分布不均匀等缺陷因素影响。在没有弹模对比测试资料时，比值n=E/Em可取1.05。因λn≠1，原级配混凝土与湿筛混凝土之间的变形特征不符合比例变形条件，两者的松弛系数不相等，即k≠km。

三、混凝土变形特性变化对测点应变和应力的影响

在坝体内部埋设应变计，将应变测点一定范围混凝土内部分粗骨料剔除，由此引起该处混凝土徐变增大、弹模有所变小，成为局部性非均质弹－粘性联体，测点的应力和变形也将异于周边远处的应力与变形。

为使问题的讨论变得简单，将测点附近剔除部分粗骨料的部位简化为一个圆核，圆核和圆外材料的弹模和徐变系数分别记为Em、φm和E、φ，研究这一非均质线弹－粘性平面联体的应力和变形。

设圆周和远处外边界受刚性约束，当物体产生一个均匀应变ε0时，圆内和圆外应力为

式中 K、Km－为圆外混凝土松弛系数和圆内混凝土松弛系数；

σr、σθ－圆周外混凝土的径向应力和环向应力，以拉为正；

σnm、σθm－圆周内混凝土径向应力和环向应力；

ε0－应变，膨胀为正。

因圆周外原级配混凝土与圆周内剔除部分粗骨料混凝土的弹模（E、Em）和松弛系数（K、Km）不同，在两种材料联结面上（r＝a）存在不平衡面力，圆内和圆周附近一定范围将发生应力和位移调整。设作用在圆周内的调整面力为qm，作用在圆外混凝土的调整面力为q，qm和q的方向以指向圆心为正向。由应变ε0及面力q、qm产生的应力如下：

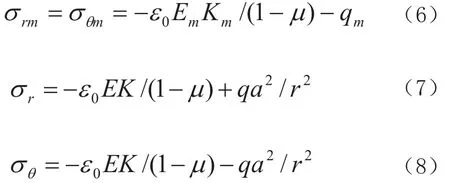
式中：a－圆的半径；

r－计算点到圆心的距离。

在联接两种介质的界面上（r＝a）径向应力相等，σrm= σr，将式（6）和式（7）代入上面的相等条件，得平衡方程如下：

由面力q和qm作用产生的位移可用下面的积分型方程表示：

式中ξ为徐变方程的积分核，其形式与变荷载（或应力）下的徐变计算法有关； u、um表示径向位移，指向圆外为正。据有关文献，对于由荷载q、qm产生的调整应力和位移计算，采用有效模量法方程式可以避开积分方程（组）的求解而又有较好的计算精度。该方法的位移方程用下式表示：

式中Ē和Ēm称为有效模量，其值为

联合求解方程（9）和方程（12），得到

将式（13）、式（14）代入式（11），消去q、qm得到应变计埋设位置（圆内）的位移um和调整应变Δεm，结果如下：

式中um负号表示方向指向圆心；Δεm负号表示压缩应变，Δεm/ε0为仅与材料变形特性有关的调整应变相对值。

下面举例说明传感器埋设位置处的应变调整，设φm=0.8、1.0、1.2，可复徐变系数取φmy=φy=0.15，灰浆率比λ=0.7、0.8，弹模比n=1.05、1.10，混凝土松弛系数K可用下面的近似公式计算：

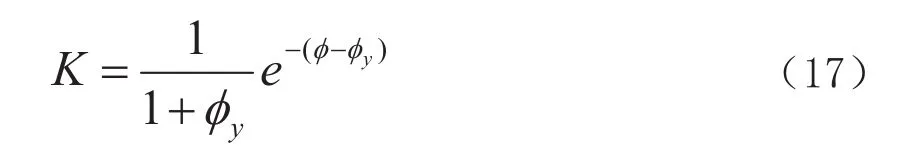
表3所列为测点混凝土压缩应变增加的相对值，说明剔除了部分粗骨料致使弹性模量下降和徐变增加后，应变计的观测值不能代表远处原级配混凝土的应变值，应作应变修正。

四、结 论

用湿筛法剔除混凝土中部分粗骨料可使徐变变形增加、弹性模量有所下降。大坝观测中埋设应变计时需将部分粗骨料剔除，这使应变计所在部位混凝土的变形特性与周围混凝土的变形特性出现差异，而两者之间的关系不符合比例变形条件，局部将发生应力应变重新调整，采用原级配混凝土的变形参数和应变测值计算观测应力的做法存在一定的偏差。本文采用大平面体中嵌入一个圆核作为计算模型，讨论两种非均质线粘－弹性组合体的应力应变调整（重分布），给出应变调整相对值与两种粘－弹性体参数之间的关系。在计算大坝混凝土的观测应力时，应依据原级配混凝土与测点混凝土之间弹性模量比n和徐变度比λ对应变测值作相应修正。

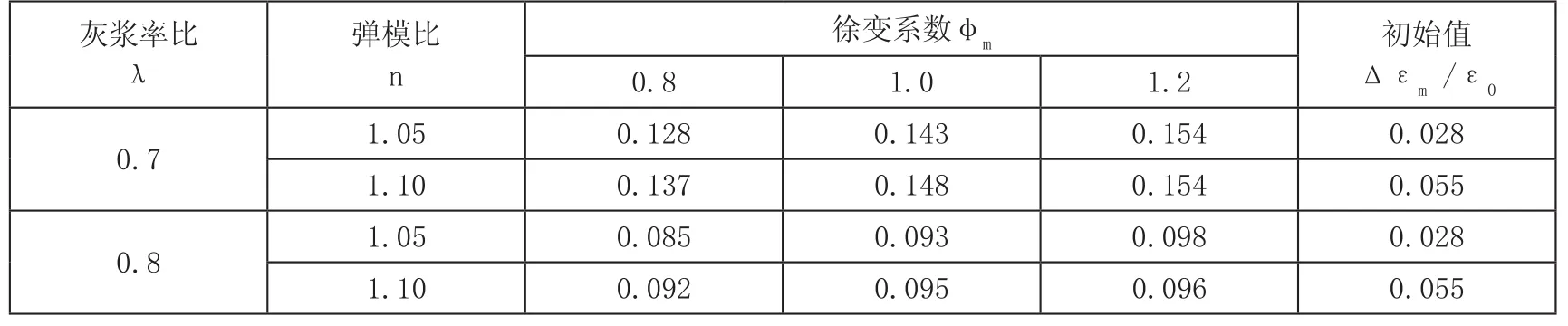
表3 传感器埋设位置应变调整值Δεm /ε0

[1] 储海宁.混凝土坝内部观测技术[M].水利电力出版社,1989.

[2] 惠荣炎,黄国兴,易冰茗.混凝土的徐变[M],中国铁道出版社,1988.

[3] 李承木.二滩拱坝原级配混凝土徐变试验研究[J].水利水电科技进展,2000.

[4] 李光伟,杨忠义,杨代六.高拱坝全级配大体积混凝土力学特性试验研究[J].2003年12月,第25卷第6期.

[5] 李光伟.长期荷载下的碾压混凝土变形特性[J].水电站设计,1997.

[6] 水利电力科学研究院结构材料研究所.大体积混凝土[M].北京:水利电力出版社,1990.

[7] 陈灿明等.大跨径桥用高强度混凝土强度与弹性模量相关性的试验研究报告[R].南京水利科学研究院,2009.

[8] 唐崇钊.用松弛代数法解粘弹性体结构的应力[J].力学学报,科学出版社,1982.

[9] 唐崇钊.混凝土的徐变力学与试验技术[M].水利电力出版社,1982.