基于三角网格的机械零件轮廓反求技术研究及系统开发

武友德，李柏林

（1.西南交通大学 机械工程学院，成都 610031；2.四川工程职业技术学院，德阳 618000）

0 引言

目前，由于产品的开发主要是借助三维 CAD系统完成产品设计过程，然后通过CAM 实现产品制造，因此，计算机辅助设计/制造/工程分析技术（CAD/CAM/CAE）的发展及应用水平成为衡量一个国家现代化的重要标志之一。然而，随着反求工程的发展在产品开发中所占的地位越来越重要，以反求工程（Reverse Engineering）、快速原型（Rapid Prototyping，简称 RP）技术为核心的产品快速开发和制造技术得到广泛的关注。反求工程、快速原型是以现有实物为基础，实现产品的快速设计与制造[1,2]。反求工程作为 RP 技术的一种重要前端处理方法和二次创新设计的重要技术手段，使得以复制设计制造为主的 RP 技术获得了再创新、再设计能力，促进了产品数字化与制造技术更紧密结合，更好地为产品再创新工程服务。

1 机械产品的特征点类型研究

反求工程中特征可定义为基于测量数据提取的用于反求工程CAD模型重建的点、线、面以及它们满足特定约束关系下的组合或复合。

机械零件产品通常是按一定特征设计制造的，特征是几何模型最原始的信息之一，反映了几何模型的设计思想。同时，特征之间具有确定的几何约束关系。因此，在反求工程CAD模型重建过程中，一个重要的目标应是还原这些特征以及它们之间的几何约束关系。目前反求工程中基于测量数据点云提取原始模型的基本特征有特征点、特征线、特征面。组成平面形状特征的截面特征间的特征点经常是曲线连续阶的变化点，根据曲线连续阶可将曲线连接点分为角点、折痕点、曲率极值点和拐点，在反求工程中基于测量数据点云获取数字化轮廓时，理想平面轮廓顶点经常退化为平滑连接，通过角点和光滑连接的识别将曲线分成基本曲线特征，实现截面特征的自动分割。

按照不同几何元素在反求工程CAD建模中的不同作用，曲线特征主要分为三类:主要曲线元、次要曲线元和辅助曲线元[3]。

2 特征点增补与相邻层间缺陷轮廓的三角网格拼接技术研究

2.1 三角网格技术

对于一般的缺陷轮廓数据，直接进行网格拼接，会因数据量大造成网格过密和计算量过大等问题，因此有必要在保证精度的前提下对此数据进行精简，以保证计算速度和效果的统一。通常的方法是找出这些轮廓点中的特殊点作为三角网格的顶点进行拼接，本项目采用的是切片轮廓数据的特征点，即角点，也可称之为拐点。它一般是由直线或曲线的交点所形成的，发生在边缘方向发生急剧变化的地方，具有局部曲率最大这一特点。因此一般可以采用基于曲率的办法来检测，这类方法的基本步骤为：1)估算图像边缘上每一点的曲率；2)找出局部曲率最大值点为待求的角点。这类方法由于要根据相邻点阵来计算曲率，就涉及微分问题，因此计算较为复杂，计算量大。此外，利用链码的特征对角点进行识别方法，由于计算简单、效果好，成为了目前研究的热点[4,5]。

2.2 链码差值对特征点的检测

为了在处理缺陷轮廓数据精简的同时，有效地保持好细小的局部特征，根据相邻点之间的链码差值对特征点进行检测。

首先，对Freeman编码后的缺陷轮廓点进行分析，可以得出如下的连续3点之间的位置关系如图1所示，从中可以看出b、c、d、e、f、g的中间点均可视为相对位置关系在中间点处发生急剧变化，因此将其视为特征点。分析其相对应的Freeman链码值，可以看出除了a中后两点的链码值差为0外，其他的后两点的链码差值分别为1、2、3、5、6、7。因此，可以根据相邻点的链码差值来快速检测特征点。

图1 链码表示相邻三点之间的位置关系

为描述方便，定义k层上第i个缺陷轮廓为Cki上轮廓点集合为{P1,P2,...,Pn}，n为轮廓点数目，Pi的链码为F(i)。则缺陷闭合轮廓点的链码差值函数为S(i)的计算方法如式(1)所示。

因此，基于Freeman链码的特点检测算法的主要步骤如下：

1）以Freeman链码的起点开始遍历链码；

2）根据式(1)计算每个轮廓点对应的链码差值；

3）记录下链码差值不为另0的轮廓点，将其视为特征点。

在检测出缺陷轮廓数据的特征点之后，可以将其它数据点删除，直接用特征点来表示该轮廓，并对其进行网格拼接，从而有效的减少轮廓数据和三角面片，以达到数据精简的目的。

对上述的轮廓数据精简结果进行存储和记录，从第一个特征点开始记录，然后依次记录方向编码和个数，即：

其中，(x0,y0)表示编码开始的第一个起始特征点，m表示该轮廓中的特征点的总个数，Oi-Ni中的Oi表示第i个特征点相对于前一个特征点的8方位Freeman位置编码，“-”表示符号，Ni表示这两个特征点之间精简去的原始轮廓点数目。

这样通过上述编码在可以很好记录轮廓数据的同时，方便快速地对轮廓参数进行计算。如两个特征点之间的距离L可以通过如下的式(2)快速方便的获得。

其中，doi表示在Freeman链码方向上的连续两点之间的距离，由于文中采用的是8方向链码，则有两类链码距离即0、2、4、6方向上链码距离l和1、3、5、7链码方向距离

根据上述的特征点检测方法对缺陷轮廓进行特征点检测和数据精简，可得如图2所示的结果，编码记录如图2所示。

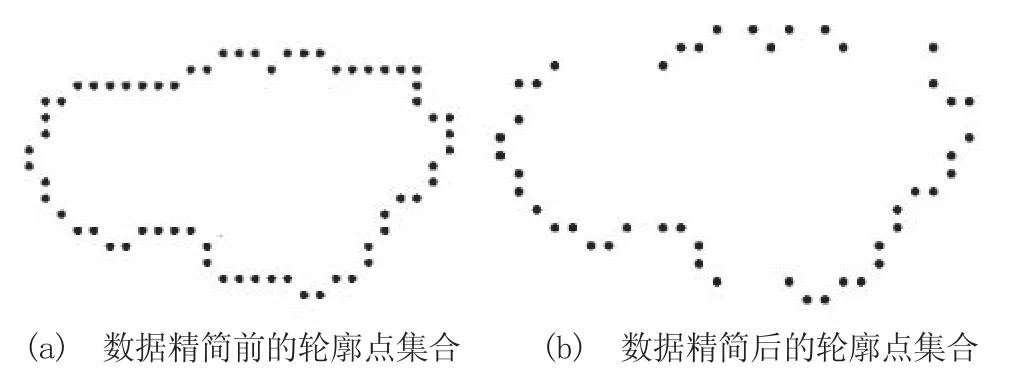
图2 数据精简

其中，(x0,y0)为起始点。

{(x0,y0)|6-5,7-1,0-1,7-1,0-5,7-3,0-3,6-1,0-3,1-2,2-2,1-4,2-4,3-2,4-7,3-1,4-4,5-1,4-1,5-1,4-2,5-1,4-3,5-1}。

2.3 轮廓特征点的确定

众所周知，在一定的层间距范围内，相邻层切片上相匹配的轮廓具有一定的相似性。但是由于缺陷的不规则性，使其难以被准确地描述。而凸包是描述二维形状的主要方法，是目前物体形状识别的有效方法之一。如果这两个相匹配轮廓相似的，那么它们的凸包也应该是相似的，可分全局对应和局部对应两步确定轮廓特征点的对应关系。

1）全局特征点对应

以k和k＋1层上轮廓Cp(k)i和Cp(k+1)j为例，通过数据精简后的轮廓特征点集合为Sp(k)i和Sp(k+1)j，用直线段连接相邻的特征点构成轮廓，然后分别求出各自的凸包CSp(k)i和CSp(k+1)j，以及求解出各自的形心，然后以各自形心为原点求出CSp(k)i和CSp(k+1)j上各点的极坐标。采用式(3)评价CSpc(k)i和CSp(k+1)j上各点的相似性。

其中：α+β+γ=1；d为CSi上第i个点与CSjp(k)p(k+1)上第j个点在断层平面上的投影距离；g为CSp(k)i上第i个点与CSp(k+1)j上第j个点间极角差的绝对值；u为CSp(k)i上第i个点与CSp(k+1)j上第j个点间曲率差的绝对值。

对于精简后的特征点的有序集合Pi(i=1,2,…,n)确定的多边形凸包轮廓，顶点Pi处的曲率ki可由相邻的三点Pi-1,Pi,Pi+1所确定的圆所决定，如图3所示。圆的曲率即为点Pi的曲率，计算公式如式(4)所示。

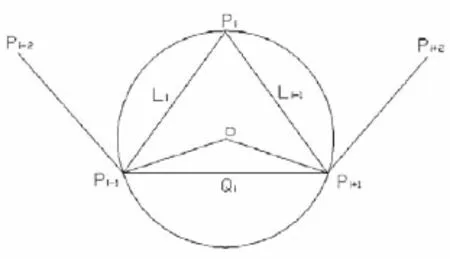
图3 曲率计算原理图

当i＝1，即Pi为轮廓点集合的起点时，由于缺陷轮廓是闭合的，在该点的曲率计算时，Pi-1可以设定为Pn即可。同样的，当i＝n，即Pi为轮廓点集合的终点时，在该点的曲率计算时，Pi+1可以设定为P1即可。

当CSp(k)i和CSp(k+1)j的形心在断层平面上的投影重合时候，d和u可以反映CSp(k)i和CSp(k+1)j上两点的相似性，利用g消除CSp(k)i和CSp(k+1)j的形心在断层平面投影上不重合的影响。当d、g和u变大时，f变小，两点的相似性变差；当d、g和u变小时，f变大，两点的相似性变好；当d、g和u均等于零时，f等于1，两点相似性最好。

在确定对应点对的过程中，首先根据CSp(k)i和CSp(k+1)j上任意两点f 值的大小，找到最相似的两点并将它们作为对应点，然后将这两个点作为起点，再进行其它相似点的匹配。采用这种方法确定的对应轮廓间的对应点称为全局对应点。确定全局对应点的过程与有向图方法相似，主要的不同点在于有向图方法找到相邻层轮廓所有点的对应点，而在确定全局对应点的过程中只确定相似性较好的点对间的对应关系。

对如图4所示的相邻两层上相匹配的缺陷轮廓的特征点的全局对应点确定试验，其结果如图5所示，其中内层为k＋1层上的缺陷轮廓，外层为k层上缺陷轮廓，两轮廓上相对应的全局对应点以直线相连。

图4 相邻两层上相匹配缺陷轮廓的特征点

图5 整体特征点对应图

2）局部特征点对应

如图4-8所示，特征点整体匹配的结果即将缺陷轮廓按照对应的特征点将其划分为多段对应的子区域。然后分别对这几段内的特征点进行相似性计算，公式如(5)所示。

其中：α+β=1；d为CSp(k)上第i个点与CSp(k+1)上第j个点在断层平面上的投影距离；u为CSp(k)i上第i个点与CSp(k)i上第j个点间曲率差的绝对值。

图6为图7经过全局对应点确定和局部对应点确定后的特征点对应结果。

为相邻两层ICT切片图像中提取出并经过上述步骤精简后轮廓点的对应关系，内层轮廓为上层轮廓，外层轮廓为下层轮廓，两个轮廓具有对应关系的轮廓点以直线方式相连接。

图6 相邻层轮廓对应点的对应关系

图7 轮廓特征点的增补结果

以图6为例，定义上层虚线连接的轮廓点集合为P={P1,P2,P3…Pn}，下层实线连接的轮廓点集合为Q={Q1,Q2,Q3…Qm}，各轮廓线上的点均以逆时针方向排列。当相匹配对应的轮廓之间的特征点不能达到一一对应的时候，如果直接对其进行拼接，则会造成一些狭长三角形和顶点过于集中的问题。因此为了有效避免此类情况的出现，根据轮廓点对应的结果，对完成整体和局部特征点对应后的轮廓特征点数据进行必要的补充和修改。其原则如下：在轮廓点对应中存在着一条直线段对应两条或以上的直线段，则依据这两条或以上的直线段在对应的直线上的投影长度的比例，在对应的直线段上插入附加轮廓点，并将这些附加轮廓点按照逆时针顺序补充到确定这条直线段的两个轮廓点中间，后面的点序号依次更新。

根据上述方法，对轮廓点集进行补充和修改，则补充后的轮廓点集合为P={P1,P2,P3…Pn…Pn+k}，Q={Q1,Q2,Q3…Qm…Qm+l}，使得(n＋k)＝(m＋l)。其中k为轮廓P中补充进去的点个数，l为轮廓Q中补充的点个数。经增补后的特征点情况如图7所示。

轮廓拼接是指用三角面片构造相邻断层上对应轮廓的表面。本项目通过利用上述特征点确定对应关系，然后用三角面片构造相邻断层上对应轮廓的表面，从而实现三维曲面的重够。

3 机械零件轮廓及曲面反求系统的开发[6,7]

研究机械零件轮廓及曲面反求系统的体系结构、系统功能和实现技术，开发出具有自主知识产权的软件平台。所开发的系统能与现有商用CAD软件集成，形成适用性强的设计开发环境。该系统的主界面如图8所示。

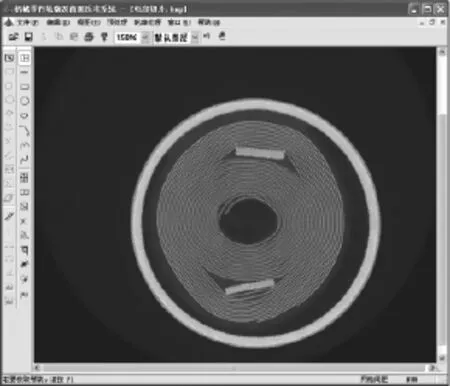
图8 机械零件轮廓及曲面反求系统主界面

对二维轮廓数据点进行的轮廓处理可实现以下功能：按向导提示的“轮廓点阵提取向导”，“轮廓点阵自动提取”，“轮廓追踪”，“轮廓自动识别”，“轮廓拟合”，“手工绘制轮廓”，“三维处理导出”等。

其中“轮廓拟合”可采用“直线拟合”，“圆拟合”，“圆弧拟合”，“椭圆拟合”，“椭圆弧拟合”，“B样条拟合”等实现任意曲面截取的二维轮廓拟合。如图9所示。

图9 轮廓处理功能

4 结论

在反求过程中，关键是如何精确地确定零件的轮廓和曲面，从而实现产品的反求设计。本项目研制开发的机械零件轮廓及曲面反求系统，为企业和研究所的人员提供一个经济高效的机械零件反求软件平台，某企业应用此技术后，大大提高设计效率、缩短设计周期,降低开发成本，增强研制产品的竞争力，从而极大地提高企业的经济效益。

[1] 李金从,邓家褆.多学科优化集成设计框架[J].现代制造工工程,2003,3:77-79.

[2] All wright S.Introduction to the MDO project.Royal Aeronautical Society MDOConference,1998.

[3] 王书河,何麟书,张玉珠.飞行器多学科设计优化软件系统[J].北京航空航天大学学报,2005,31(1):51-55.

[4] Stephen M.Batill, Marc A.Stelmack,Xiong Qing Yu.Multidisciplinary design optimization of an electric-powered unmanned air vehicle[J].Aircraft Design, 1999,2:1-18.

[5] 陈琪锋,戴金海.多目标的分布式协同进化MDO算法[J].国防科技大学学报,2002, 24(4):12-16.

[6] Ting-Yu Chen,Chen-Ming Yang.Multidisciplinary design optimization of mechanisms[J].Advances in Engineering Software,2005,36:301-311.

[7] Marc A.Stelmack,Stephen M,Batill,Bryan C.Design of an Aircraft Brake Component Using an Interactive Multidisciplinary Design Optimization Framework[J].Transactions of the ASME,2000,122:70-77.