数控铣床直线定位精度检验方法的理论分析

彭 巍，秦启书

（河南工业职业技术学院，南阳 473009）

0 引言

数控铣床的主要技术参数和技术指标很多，其中静态定位精度非常重要。静态定位精度主要包括；直线定位精度；分度定位精度（四轴）；失动；重复定位精度；零点定位精度；脉冲步距精度。直线定位精度，直线定位精度是数控铣床最基本的也是最重要的参数之一，无论是数控铣床的出厂检验还是用户的验收检验都要进行。

1 数控铣床的直线定位精度检验方法和步骤

1）在行程全长上选若干测量点，一般总行程在500 mm以下的，每50 mm设一测量点。总行程在500 mm以上的铣床，每100 mm设一测量点。如果行程特别长，则测量点的间隔可以取的更大一些。总之间隔范围可在50～200 mm之间选取。

2）在检测时应以不同的进给速度移动，对各测量点进行位置测量。

3）单项移动测量法如图1所示。

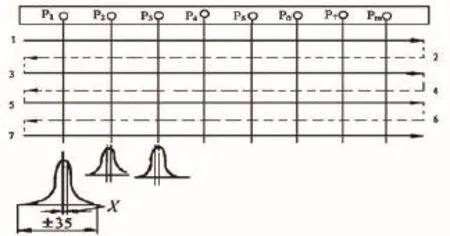
图1 单向移动图

4）双向移动测量法如图2所示。

5）测量时的注意事项。

测量中重复次数愈多，则测量精度愈高。通常最多次数不超过7次，因为次数过多，工作量太大。一般数控机床的直线定位精度在土0.015～0.02 mm范围内。

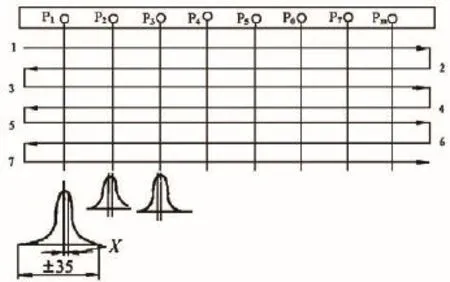
图2 双向移动图

2 测定后的数据处理和分析

1）精度曲线法

进行定位精度检验时，先按规定的测量点间距编制程序，控制机床工作台，然后实测各个测量点的位置，若实际位置与给定位置的偏差为Xi,则在pi个测量点上可得到N个检验偏差值。分布为正态曲线，可按下式求出均方差值。

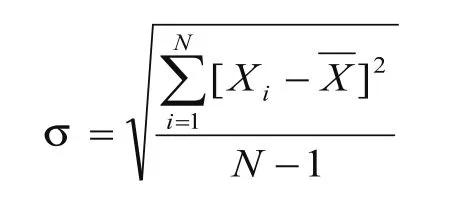
式中 ：

Xi—某测量点的各次测量误差值；—实测误差值的算术平均值；

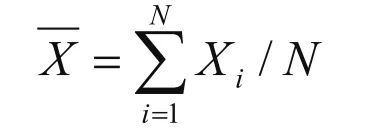
N—重复测量次数。

这里需要说明以下几点：

（1）由于检验中影响因素较多，有些并未完全考虑进去，故将σ值取大一些。

（2）σ值的物理意义表示误差的分散程度，σ值愈大，误差分散愈大，表示尺寸不准确；σ值愈小，误差比较集中，因此尺寸比较准确。

（4）按照行程次序，画出各测量点的正态分布曲线，即可得到机床的精度分布曲线图，如图3所示。

（5）从精度分布图上找出上、下极限值，即所有正态分布曲线的最大值与最小值，它们之间的距离就是定位精度。通常以上、下极限值的中心点为理论给定值，用对称公差表示，如图3所示。

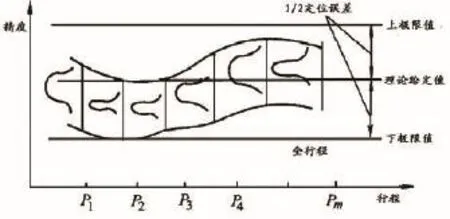
图3 精度分布曲线图

（6）通过精度分布曲线图可以分析各测量点的误差，因此易于找出影响定位精度的原因，采取措施，提高机床定位精度。

2）折线极限法

（1）重复测量各点的实际值，并算出误差的平均值 χ1，χ2，χ3……χn，则误差就是实际值与给定值之差。

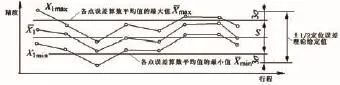
图4 平均值分布曲线图

（2）将差值按行程长度画在图上(如图4所示)即可得到误差平均值的最大值 χmax和最小值χmin。它们之间的范围S就表示了各测量点误差平均值的分布状态，也就是系统误差的偏差值大小。

（3）同时，记录下各测量点实际值与给定值相差的最大值 χimax和最小值χimin，即各测量点误差的最大值和最小值，从而得到各测量点的误差分布范围Ri：

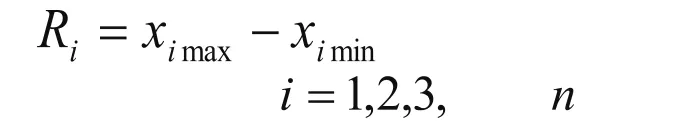
（4）可由Ri用统计数学理论算出均方差值σi：

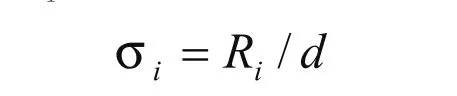
式中d为系数，表示一组数据中χimax，χimin，Ri及σ的关系。可由专用表格中查出(见表1)。

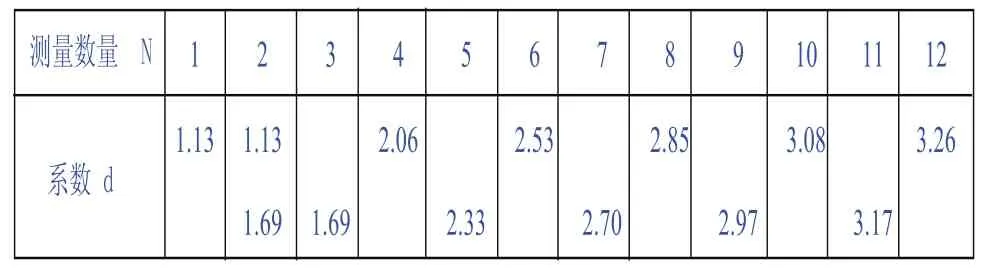
表1 系数d与测量次数的关系

（5）d愈大则σ愈小，说明此组数据多因此就愈精确，N即表示此组数据的测量次数。一般测量次数不超过12次。故表1中只将N列到12次。

（6）为简化计算，先算出各测量点的误差分布范围Ri的平均值R:

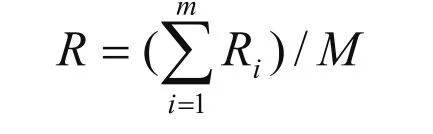
式中M为测量点数，再由σ=R/d得到均方差值σ。

（7）±3σ为偶然误差的分布范围，将 χmax和χmin之间的范围S与±σ合在一起，便是整个的定位误差，以S的中点为理论给定值，则定位误差为。±1/2(S+6σ)

（8）这种方法由于比前一办法计算简单故易于推广，但精度较前者为低。

3）统计曲线法

（1）记录下所有测量点多次测量的数据，分别与其给定值比较，得出差值，总共可得到M.N个数据，将它们按误差值的大小分组，便可得到直方图(如图5所示)，它表示了这个误差值的分布情况。

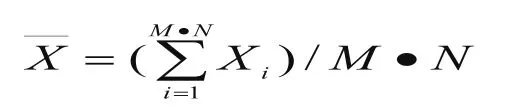
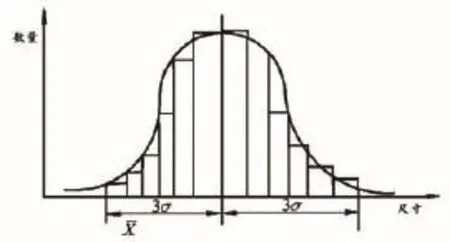
图5 分配曲线法误差分布图

它表示了系统误差的偏差，即误差值分布中心与给定值的距离。

（2）算出均方根值σ：

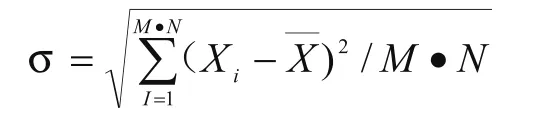
±3σ表示偶然误差的分布范围X=±3σ表示了整个的定位误差，可画其误差分配曲线(如图5所示)。这种方法比较简单，而且比较准确，但它不能看出其各测量点的误差的分布情况，所以不便于分析误差发生的部位和影响因素。作为数控机床的出厂检验，是一种可行的方法。

在画直方图和分配曲线时，按误差值大小分组的组数与数据个数有关，一般推荐如表2所示。

上述的几种测量直线定位精度的方法，可以用标准的表格和绘图来记录，这样在处理数据时比较方便、迅速。

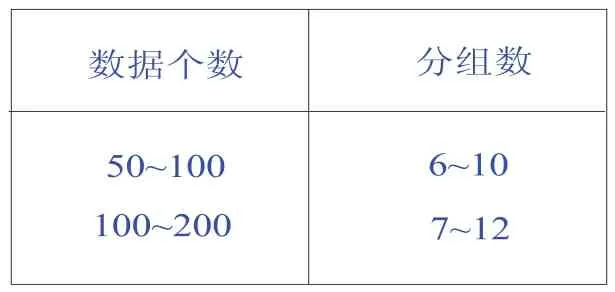
表2 推荐数据表

3 结论

1）测量点越多，检测精度越高，但是需要的时间很长，同时需要同类仪表数量太多。

2）利用精度曲线法进行数据处理，所得测量结果直观，便于查出引起误差的原因，所得的误差取值范围较大，结果可靠程度高。适合机床厂商生产过程精度检验。

3）利用折线极限法进行数据处理，数据计算简单，无需绘制正态分布曲线，看不到个点和整体的误差分布情况。可以作为数控机床的用户检验。

4）统计曲线法比较简单，而且比较准确，但它不能看出其各测量点的误差的分布情况，所以不便于分析误差发生的部位和影响因素。作为数控机床的出厂检验，是一种可行的方法。