空压机时变模型的建立与预测控制方法的研究
王盛慧, 金 星, 田 巍
(1.长春工业大学电气与电子工程学院,吉林长春 130012;2.中国人民解放军装甲兵技术学院电子工程系,吉林长春 130117)
0 引 言
深冷空气分离技术是在高压状态下,将作为原料的空气液化,依据气、液浓度以及气体沸点的差异,分离出氧气、氮气等其它气体的精馏生产工艺。深冷空气分离系统由空气净化及压缩单元、冷凝及精馏单元、产品输送和贮存单元组成[1],如图1所示。
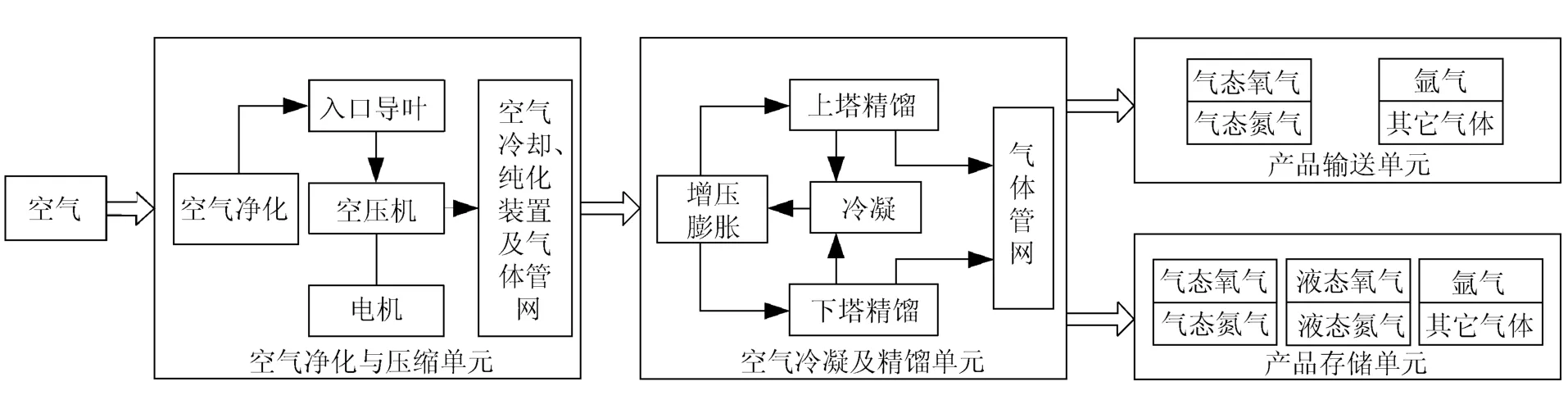
图1 深冷空气分离装置系统框图
其生产过程的控制要点是保证空气压缩机恒压输出,使空气压缩物流变化与生产负荷保持一致,不仅有利于上、下精馏塔中气氮冷凝、液氮分离、富氧液空提纯,而且有效地达到节约能源的目的[2]。因此,空压机恒压控制是高质量空气分离技术的关键[3-5]。
1 空压机的调节结构
空压机恒压控制是通过调节同步电机的转速实现的。监测供气管网压力的变化,调节电机给定电流,改变转速,控制空压机单位时间的出风量,从而达到总管管网压强恒定的目的。由于管网压变阻力惯性比较大,当检测电网谐波引起电机频率的扰动或用户用气量的变化而导致管网压强变化后,再通过PID调节器抑制频率或压力扰动,此期间空压机装置系统内管道、管件的压力和管内空气流量的变化可能已经出现大幅偏差,因而,无法达到恒压调解过程平稳、迅速的要求。尤其在下塔液氮回流、富氧液空提纯阶段,管网压力的波动极易造成气体精馏纯度的变化。
空压机恒压调节控制系统采用主、副串级调节结构,如图2所示。
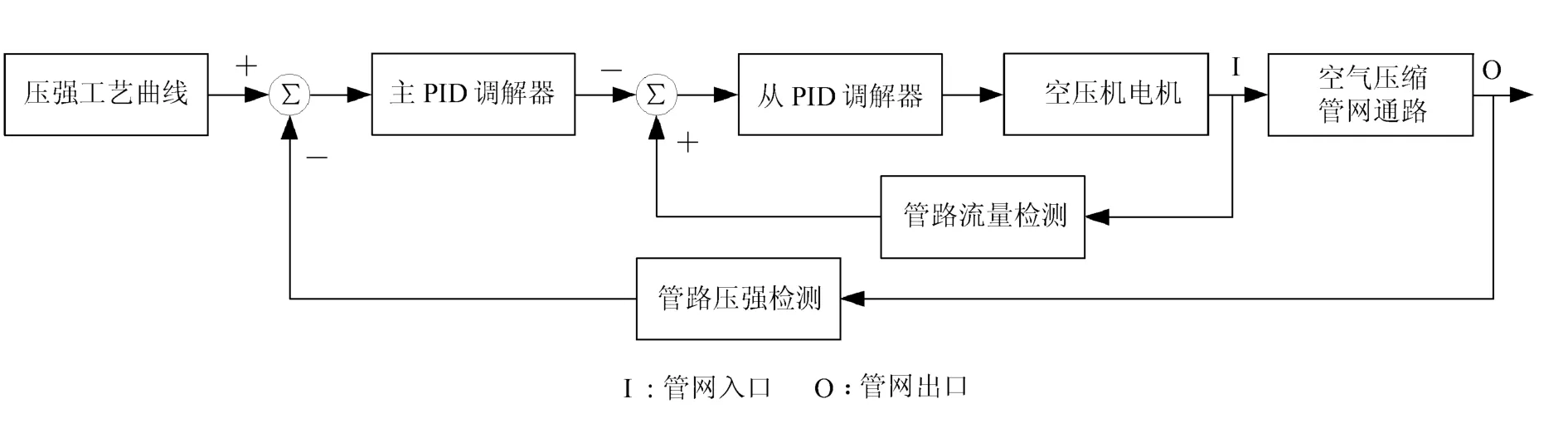
图2 空压机恒压串级控制系统框图
在主控制调节回路中,压力变送器检测管网出口压力,与生产工艺压强设定值比较得到压强偏差,作为主调节器调节空压机的给定,并作为副环调节器的设定值输出。在副控制调节回路中,副调节器的被调参数来自管网流量与转速之间的对应关系,抑制流量扰动对管网压力产生影响,调节管网压强满足工艺设定值要求。
2 空压机时变模型的建立
基于串级控制的空压机调节系统,采集到的现场管网排气量、压力、流量等数据本身并不满足彼此统计独立,存在一定的数据自相关,利用近似线性化传递函数模型所设计出的PID调解器,会造成系统稳定精度较差,动态品质、控制效果不理想等问题。文中基于空压机装置特性曲线,结合数据自相关现象,将空压机系统数学模型转化为一种受控自回归积分滑动平均CARIMA(Controlled autoregressive integrated moving average)模型,设计目标函数,计算相关矩阵,优化空压机系统预测控制律,实现空压机的自动化控制。
2.1 空压机CARIMA模型
设定空压机装置控制系统中,管网是指压缩机后面背压系统的管路、排气管路以及管路上的附件、设备等全部装置。因而在研究空压机与其管网压强关系时就可忽略空压机进气情况,使问题得以简化[6]。管网入口I和出口O之间根据流动系统机械能守恒,列出伯努利方程。
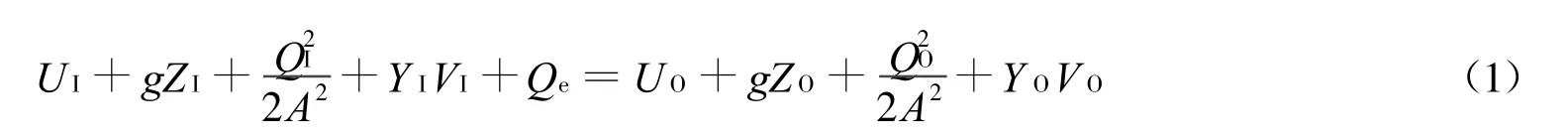
式中:UI,UO管网入口和出口管道内气体内能;
ZI,ZO管网入口和出口管道升举高度;
QI,QO管网入口和出口管道内气体流量;
YI,YO管网入口和出口管道内静止压强;
VI,VO管网入口和出口管道内气体体积;
Qe气体管路内获得的热能。
气体流经管网过程中,内能U的变化与气体压力、流量、温度有关,由物化关系得出:
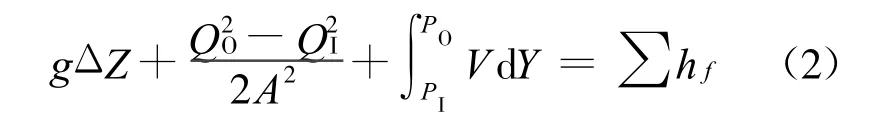
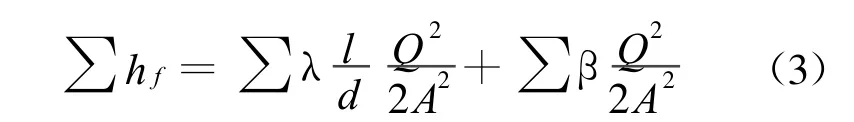
忽略气体体积、密度的变化,空气密度ρ为常量。
则:
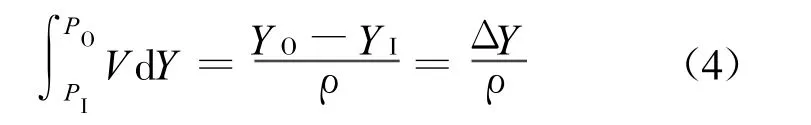
将式(3)和式(4)代入式(2)得:
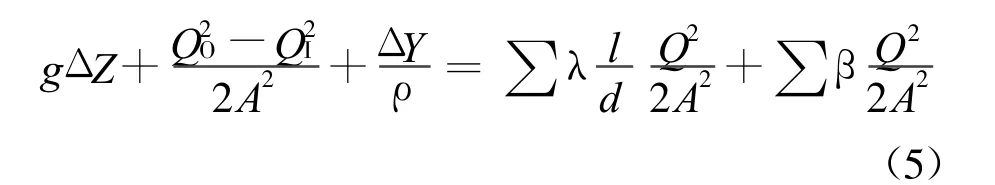
可见,流量Q的大小与Δ Y的变化并非标准的线性关系,而存在明显的时变、非线性。根据空压机系统运行特性,空压机转速N与流量Q成正比,则管网压强Y与流量Q的关系可转化为管路压强Y与空压机转速N之间的关系,建立动态方程:
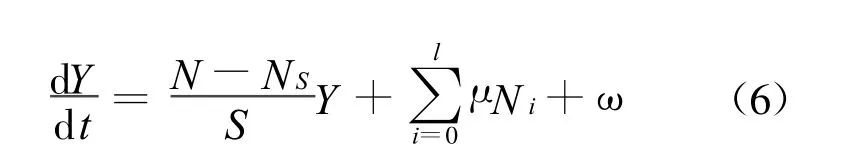
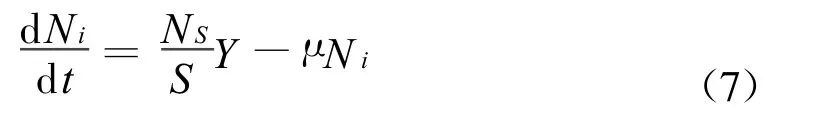
i=1,2,…,n
YS最终控制目标,管路压强恒定值;
NS当实现管路压强恒定在Y=YS时的电机转速;
式(6)可进一步整理:
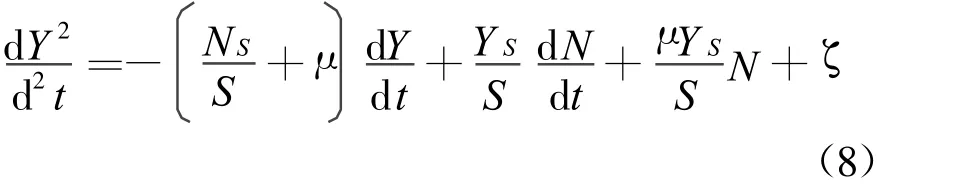
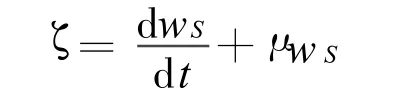
设ζ为白噪声干扰。将式(8)离散化得:
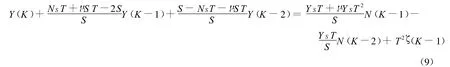
由式(9)可建立起CARIMA模型[7-9]:
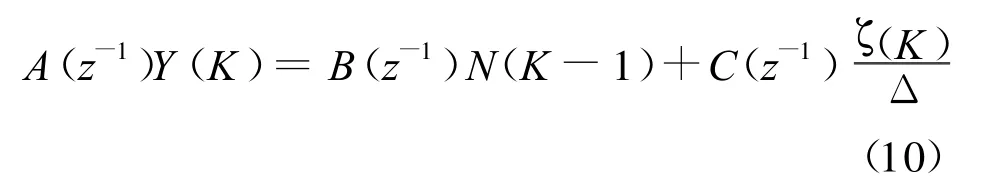
其中:
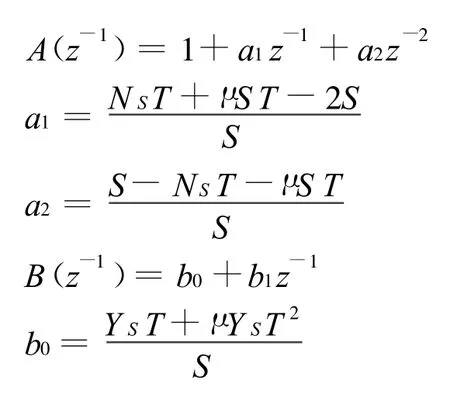
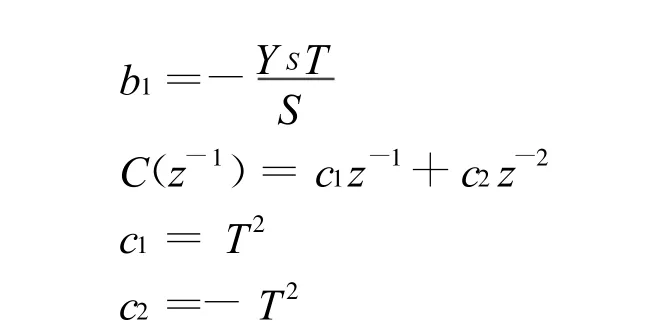
式中:z-1离散系统的后移算子;
2.2 参数估计
对包括副回路在内的广义对象建立CARIMA模型,选取目标函数:
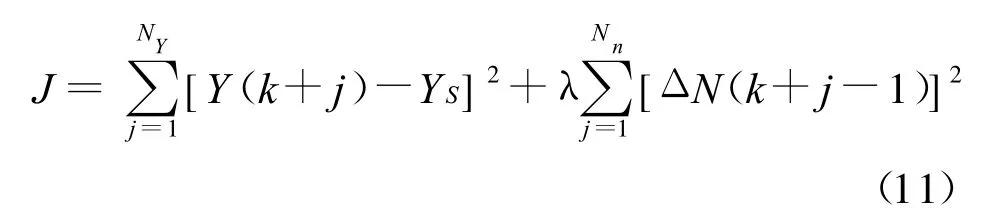
式中:NY输出预测时域长度;
引入Diophantine方程,则广义预测控制律为:
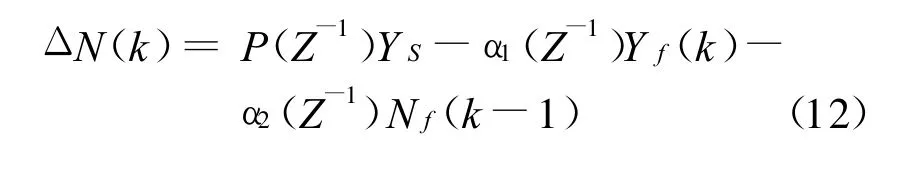
其中:
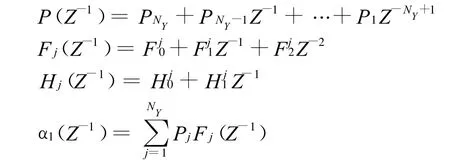
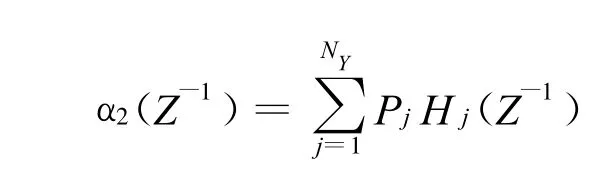
方程解的递推形式为:
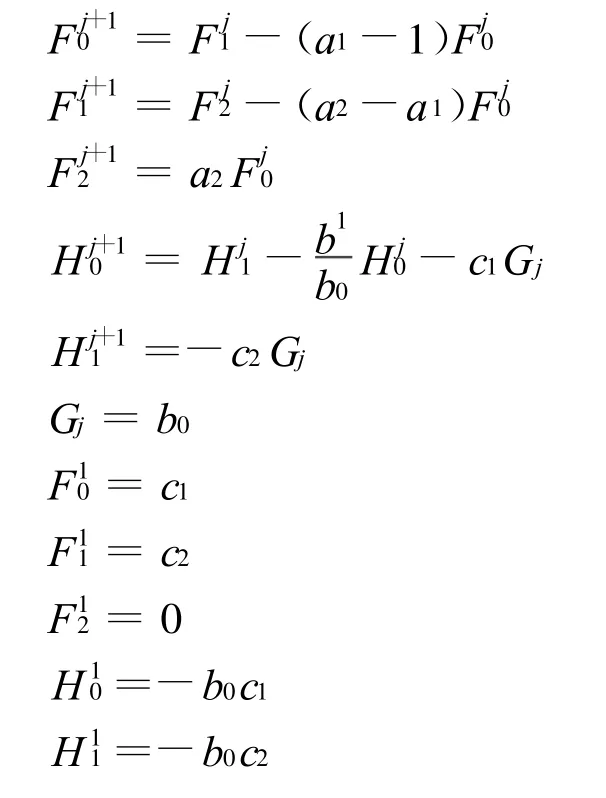
3 现场数据分析
某化工厂深冷空气分离装置选用排气量为32 000 Nm3/h的离心式空压机,其配用电机3 400 kW,管网气体压强运行范围为≤0.58 MPa,波动范围不能超过±0.02 MPa,排气温度≤100℃,不间断运行。
以某日空气压缩参数为例,管网入口初始压强为0.5 MPa,负荷为80%。由于产排量的增加,负荷增加至85%,空分设备变负荷运行,调整曲线如图3所示。
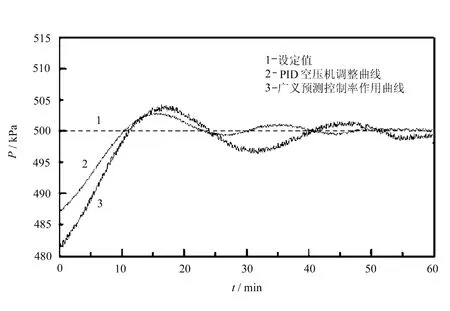
图3 空压机变负荷运行调整曲线
图3记录了现场管网压强与记录时间之间的变化关系。
现场数据分析如下:
(1)空压机变负荷调整过程,广义预测控制率与PID控制相比,在管网压强波动范围方面有明显的优势。曲线2在空压机负荷增加5%时,输出管网压强下降至0.482 MPa,而曲线3则接近0.487 MPa。两者比较,曲线3波动幅度减小28%。这不但减少放空阀打开的机会,保护空压机不发生喘振,而且能量损失也会随之而越少,达到节约能耗的目的。
(2)空压机变负荷调整过程,广义预测控制率与PID控制相比,管网压强调节时间短,调节平和。由于现场电网谐波影响,电流存在随机干扰,管网沿程摩擦阻力损失和局部阻力损失等因素,曲线2调整管网压强至稳定大约需要50 min,而曲线3则仅需要35 min,调整时间减小30%。如按全年无休运转8 760 h,功率因素0.85,仅变工况调整电机稳定工作大约可节电4%,约1.12万kW◦h。
4 结 语
遵循深冷空气分离工艺,在分析空压机运行特点和各主要参数变化规律的基础上,克服现场数据间的相关性、非线性和不确定干扰因素,将空压机系统数学模型转化为一种受控自回归积分滑动平均CARIMA模型,以管路气体压强充分逼近设定值、电机转速变化量尽量小为目标函数,引入Diophantine方程,运用递推、差分运算,获得广义预测控制律。以空压机系统现场采集的管网排气量、压力、流量、电机转速等数据为参考,建立的空压机时变模型和控制策略,与PID控制系统调节相比,能有效消除非线性和不确定干扰对空压机恒压调速系统的影响,系统调节过程平和,控制精度、动态品质有所提升,实现了对空压机的优化控制,降低系统能源消耗,保证了氧气、氮气等产品质量。
[1] Li Guilan.The theoretical and experimental research on operation energy saving technology of Type DH-71 centrifugal air compressor[J].Sichuan University,2005(2):13-40.
[2] 刘克平.吉林省节能监测服务技术体系建设意义及对策[J].长春工业大学学报:自然科学版,2007,28(1):42-45.
[3] 邹正文,邹晓东,周耀密.离心式压缩机叶轮抛光的节能原理及应用[J].风机技术,2001,6:23-27.
[4] 李海根.离心式压缩机节能改造综述[J].大氮肥,2001(2):77-80.
[5] 黄钟岳,王晓放.透平式压缩机[M].北京:化学工业出版社,2004:1-155.
[6] 王荣祥,郭业兵,张永鹏,等.流体输送设备[M].北京:冶金工业出版社,2002:125-260.
[7] Qin S J,Badgwell T A.A survey of industrial model predictive control technology[J].Control Engineering Practice,2003,11(7):733-764.
[8] Li Qi-An,Chu Jian.M ultivariable generalized predictive control for diagonal CARIMA model[J].Journal of Zhejiang University:Engineering Science,2006,40(4):541-545.
[9] SHI Xiao-ping,ZHU Yi.Study on generalized predictive control for the neutron flux density of the nuclear reactor[J].Atomic Energy Science and Technology,2003,37(4):340-344.

