一种支持纸的折叠、剪切与展开的计算模型

刘金义， 张笑伶

（辽宁石油化工大学计算机与通信工程学院，辽宁 抚顺 113001）

儿童剪纸是培养儿童动手能力、开发儿童空间想象力的极好手段，现已成为国内许多中小学的手工活动课程内容。儿童剪纸的典型过程为[1]：从初始的一张正方形或长方形的彩纸开始，经过若干次的折叠，再以一剪或多剪方式剪去纸的一部分，最后将剩余部分展开，得到各式各样的平面形象。“剪五角星”相信是许多人都经历过的最经典的儿童剪纸过程。本文所关心的问题是，一张纸经过多次折叠和剪切，展开后所得的形状是什么？这个问题是开发一个计算机辅助儿童剪纸方案设计系统必须解决的问题。

与本文关心的问题相近的一个领域是儿童折纸(origami)的设计。该领域对纸的操作只有折叠并且允许一些非简单的复杂折叠。关于计算机辅助折纸设计，已有许多相关的研究，例如，如何在数学和算法上描述折纸和定义折叠过程[2-3]，给定一张纸的折痕如何判断它是否对应一个合法的折纸作品[4]，特别是 Kishi等开发了一个可以交互进行折叠操作并进行动态演示的网站[5]。与本文关心的问题相近的另一个领域是中国传统民间剪纸的设计。该领域对纸的操作只有剪切（实际上叫“刻”操作更合适，因为它允许生成孔洞），所以一般都把民间剪纸设计看成是一个平面设计问题，研究的重点放在如何生成典型的纹样方面，而不关心它们是如何剪出的[6-7]。

为了开发一个既能进行儿童剪纸方案设计又能向儿童演示典型折剪过程的程序，作者设计了一个能够支持折叠、剪切和展开操作的计算模型，设计了模型的具体数据结构以及相关功能的实现算法，并且按照该模型开发了初步的原型软件Virtual Paper。本文的第1节将给出相关的约定与术语，第2节将介绍这个模型的具体数据结构，第3节将介绍在这个模型中相关功能的实现算法，第4节给出由Virtual Paper生成的一个折剪实例。

1 基本约定与术语

为了建模的需要，计算机对虚拟纸张的操作与人对真实纸张的操作应该有所不同，为此需对虚拟纸张和其上的操作做出约定并且给出相关术语。这些约定与术语大部分与前人文献相同[2-4]。

首先，参与折剪的虚拟纸是没有厚度的平面多边形，分为正面与反面，两面的颜色可以不同。在折叠过程中，折出的页片(facet)也看作平面多边形，它们的面积总和与初始纸张的面积相等，即不考虑由于折痕造成的面积损失。

对于折叠操作，目前只考虑简单折叠(simple fold)，即一次折叠只能沿着一条直线进行。把这条直线叫做折叠线(folding line)，它把相关页片分成2个页片，使得其中一个绕着折叠线向上或向下旋转180°。如果是向上折叠，则相对于原页片的上面产生一条沟谷折痕(valley crease)；否则，产生一个山峰折痕(mountain crease)。约定折出的页片相互贴合在一起，之间距离为0。

把初始纸张经过折叠、剪切和展开能够达到的状态叫做一个纸态(paper state)。值得注意的是简单折叠所能达到的纸态是受限制的，图1给出的纸态就不能通过简单折叠获得。但是大部分儿童剪纸都采用简单折叠。

对于剪切操作，约定它是剪刀的“剪”而不是“裁”或“刻”，剪切轨迹只能是一条开曲线。剪切后，页片之间可以是一体的也可以是分离的。约定折叠操作和剪切操作可以任意组合，但是对于展开操作，一旦展开后，就不再进行折叠和剪切。

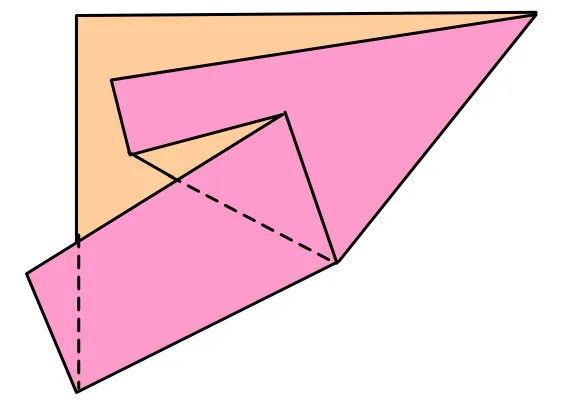
图1 不能通过简单折叠获得的纸态

2 数据结构

2.1 设计目标

数据结构是一个人机交互系统的计算模型的核心。它的设计目标就是要满足儿童剪纸方案的交互设计以及经典折剪方案演示的需要。具体地说，必须能够支撑下面基本功能：

（1）每当一个操作完成后，可以立即显示出当前纸态的真实效果图。这个效果图可以是二维的，但是应该消除隐藏线。

（2）根据需要，可以以动画形式展示操作过程。

（3）在纸张展开后，仍然保留折痕痕迹，且区分山峰折痕和沟谷折痕，以便用户详细考察折叠机理。

（4）整个折剪方案可以被记录下来，存储成文件，以满足批处理演示的需要。

2.2 问题分析

这里需要进一步澄清折叠、剪切和展开3种操作，然后导出哪些信息是计算模型所必需的。

首先考察初始纸态经过m次折叠、n次剪切的任意组合到达某纸态的过程，图2给出了这个过程的一个例子。在图中，对于任意0≤i≤m及0≤j≤n，Si,j表示初始纸态经过i次折叠和j次剪切所获得的纸态，其中S0,0是初始纸态。纸态的变化是通过如下折叠变换与剪切变换完成的

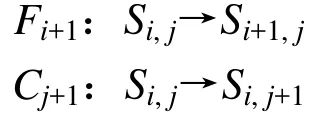
观察 1 给定当前纸态 Si,j的合理表示及折叠变换Fi+1的完整描述，则下一纸态Si+1,j是可计算的；给定当前纸态Si,j的合理表示及剪切变换Ci+1的完整描述，则下一纸态Si,j+1是可计算的。

再考察展开过程，仍然参见图2的例子。展开变换可以看成折叠的逆变换

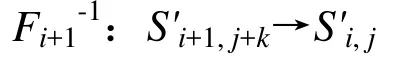
其中 S'i,j为与Si,j对应的纸态，S'm,n＝Sm,n，S'0,0是最终所要的平面纸态。

图2 一个具有4次折叠和2次剪切的组合及其展开

观察2 如果从Si,j到Sm,n的过程中没有剪切操作，即 j＝n，那么除了保留一些折痕外，S'i,j与Si,j的形状相同。

观察3 对于任意k≥0，如果给定当前纸态S'i+1,j+k的合理表示及折叠变换Fi+1的完整描述，那么S'i+1,j+k展开后的下一纸态S'i,j是可计算的，而与Si,j到Si+1,j+k之间的k个剪切变换无关。

根据前面的分析，模型中保存一份当前的纸态Si,j或S'i,j是必需的。为了实现展开变换，还需要顺序记录全部的折叠变换F1～Fm。但是为了能够把完整的折剪方案存储成文件，剪切变换C1～Cn也需要被顺序记录。

总之，为了目标要求，计算模型的数据结构应由2部分组成：一是当前纸态的表示，二是全部折剪操作及其顺序的保存。这2部分不是孤立的，只有互相联系在一起才能实现展开功能。

2.3 纸态的表示

纸态是一个特殊的几何实体，是页片以及它们之间拓扑邻接关系的集合。一个页片的几何形态就是一个多边形，如果单纯从描述的角度，把它表示为顶点的列表即可，但是考虑到页片在折叠和剪切的过程中是动态的，所以参照实体几何模型的半边表示法[8]，增加了半边节点(即有向线段)。这样一个页片就表示为一系列首尾相接的半边。这里与二维流形体的半边数据结构有所不同是没有Edge节点，但是增加了一个与其相近的Crease节点。一个Crease也由2条半边构成，但是只有折叠形成的半边才有对应的 Crease。Crease节点的加入可以方便折叠与展开的实现以及折痕的显示。

struct Vertex

{

int vertexID; //顶点标号

float coord[3]; //z坐标是为了三维夸张显示的需要

};

struct HalfEdge

{

HalfEdge *prv, *nxt; // 前驱与后继半边

Facet *ownerf; //所属的页片

Vertex *startv; //起始顶点

Crease *crease; //所对应的折痕，可以是NULL

};

struct Crease

{

HalfEdge *he1, *he2; //对应的2条半边

char mv; //折痕的属性(相对于he1与he2所属页片的正面)：

//山峰为1，沟谷为-1

};

struct Facet

{

int faceID; //页片的标号

int layer; //页片的层次优先级

char direct; //页片的方向：正面朝上为1，否则为-1

HalfEdge *he; //页片的任一半边

};

list facets;

list creases;

一个几何模型中最重要的内容是拓扑关系的表示，但是严格地表示纸态中页片之间的重叠与邻接关系是非常困难的。幸运的是，本文目前关心的纸态中的页片都是通过简单折叠产生的，所以可以根据折叠顺序为每个页片赋予一个唯一的层次优先级（展开后可以存在优先级相同的页片），以整数形式存储在Facet节点中。

例1 图3中的纸态由3个页片、12条半边、8个顶点和2条折痕构成。页片f1的层次优先级为0。页片f2与f3尽管互不重叠，但它们的优先级是不同的，取决于折叠顺序。如果先叠出f2后叠出f3，则f2的优先级为1，f3的优先级为2。

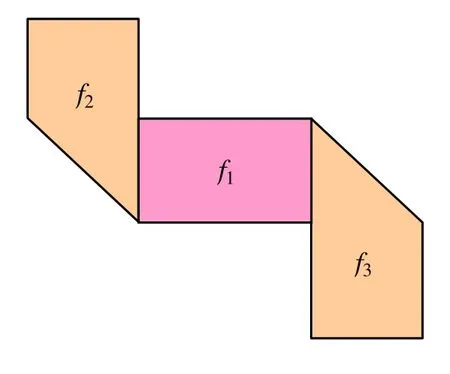
图3 一个纸态

2.4 折剪过程的记录

全部折叠和剪切操作最适合被顺序地记录在一个栈中，栈的每一项对应一次操作。为了将来能够顺利实现展开功能，如果一个操作是折叠，那么在节点中需记录哪些新产生的页片被旋转。下面代码中的列表 rot_facets就是为了完成此目的。值得注意的是，一个折叠操作的rot_facets内容是动态的。如果以后的折叠操作将前面 rot_facets的某个页片分割，就应该用分割出的2个页片替代该页片。如若不然，在展开时一定会少恢复一些页片。

struct Operation

{

char op_type; //操作类型：折叠为0，剪切为1

union {

list cut_path; //剪切轨迹

struct Fold{

float fold_line[3]; //折叠线的方程

char fold_mode; //向上还是向下折叠

list rot_facets; //折叠中被旋转的页片

} fold;

};

};

stack operations;

3 实现相关功能的算法

这里给出一般情况下相关功能的算法步骤，由于篇幅限制，不对退化情况进行详细讨论。

3.1 折叠操作

给定折叠线的描述并且指定参加折叠的页片，折叠操作可以通过如下4步实现：

Step 1 对于每个将被折叠的页片，计算它们与折叠线的交点，通过增加顶点和半边，把交点变成页片的顶点。

Step 2 用折痕及其对应的半边连接交点，把每个页片分割为 2个或多个页片。（如果被折叠的页片是凹的，可能产生多个页片。）

Step 3 按照事先约定的原则，将折叠线某侧的页片做旋转，计算旋转后的顶点坐标，更改页片的方向属性。

Step 4 更新页片的层次优先级。更新的原则是：如果是向上折叠，则把参与旋转的页片的当前优先级颠倒，然后把它们放在最高层次；如果是向下折叠，则也把参与旋转的页片的当前优先级颠倒，然后把它们放在最低层次。

Step 5 遍历前面已记录的每个折叠操作，查找它所旋转的页片是否包含当前被分割的页片，如果包含，则将分割后的页片替换分割前的页片。

3.2 剪切操作

给定剪切路径的描述，剪切操作可以由如下3步实现：

Step 1 按照事先约定的原则，把用户输入的剪切轨迹的外侧做成一个足够大的多边形PCUT。

Step 2 对于当前纸态中的每个页片，做该页片与多边形PCUT的布尔减运算。

Step 3 对于当前纸态中的每条折痕，把它作为一条线段减去多边形PCUT，如果该折痕没有被全部减掉，则合成剩余折痕的半边。合成的方法是根据坐标匹配原则，即如果某剩余折痕的2个端点与该折痕两侧页片的某2个半边的坐标相同，则将该折痕与这2条半边关联在一起。

3.3 展开操作

尽管通常仅需要最终的展开纸态，但它必须是逐步获得的。在当前纸态的基础上进行一次展开，可以通过下述步骤完成：

Step 1 从折剪操作栈中弹出一个操作，如果操作为空(到达栈底)，则结束；否则如果该操作是折叠操作，则转到Step 2；如果该操作是剪切操作，则继续Step 1。

Step 2 把 rot_facets中记录的页片做反向180°旋转，计算旋转后的顶点坐标，更改页片的方向属性。

Step 3 重新设置参与旋转页片的层次优先级。

3.4 显示算法

因为记录了页片的层次优先级，所以对纸态进行二维真实感显示变得非常简单，画家算法即可完成此工作：首先对全部页片按照层次优先级由小到大的顺序进行排序，然后顺序以实心填充的形式画出每个页片内部，以不同的线型或颜色画出它的边界线和折痕线。

4 应用实例

按照本文给出的计算模型，以Visual C++ 6.0为开发工具，实现了一个即可以进行儿童剪纸方案设计又可以展示已有折剪方案的原型软件，命名为Virtual Paper。目前该软件还是一个纯二维的，没有提供操作的动态演示功能。在折叠操作的人机交互方面，用户除了可以任意设计折叠线外，还可以采用“沿对角线折”、“二等分对边折”、“二等分角折”等非常常用的经典折叠命令。图4给出了在该软件内进行折剪窗花的过程。注意在展开图中区分了2种不同类型的折痕。

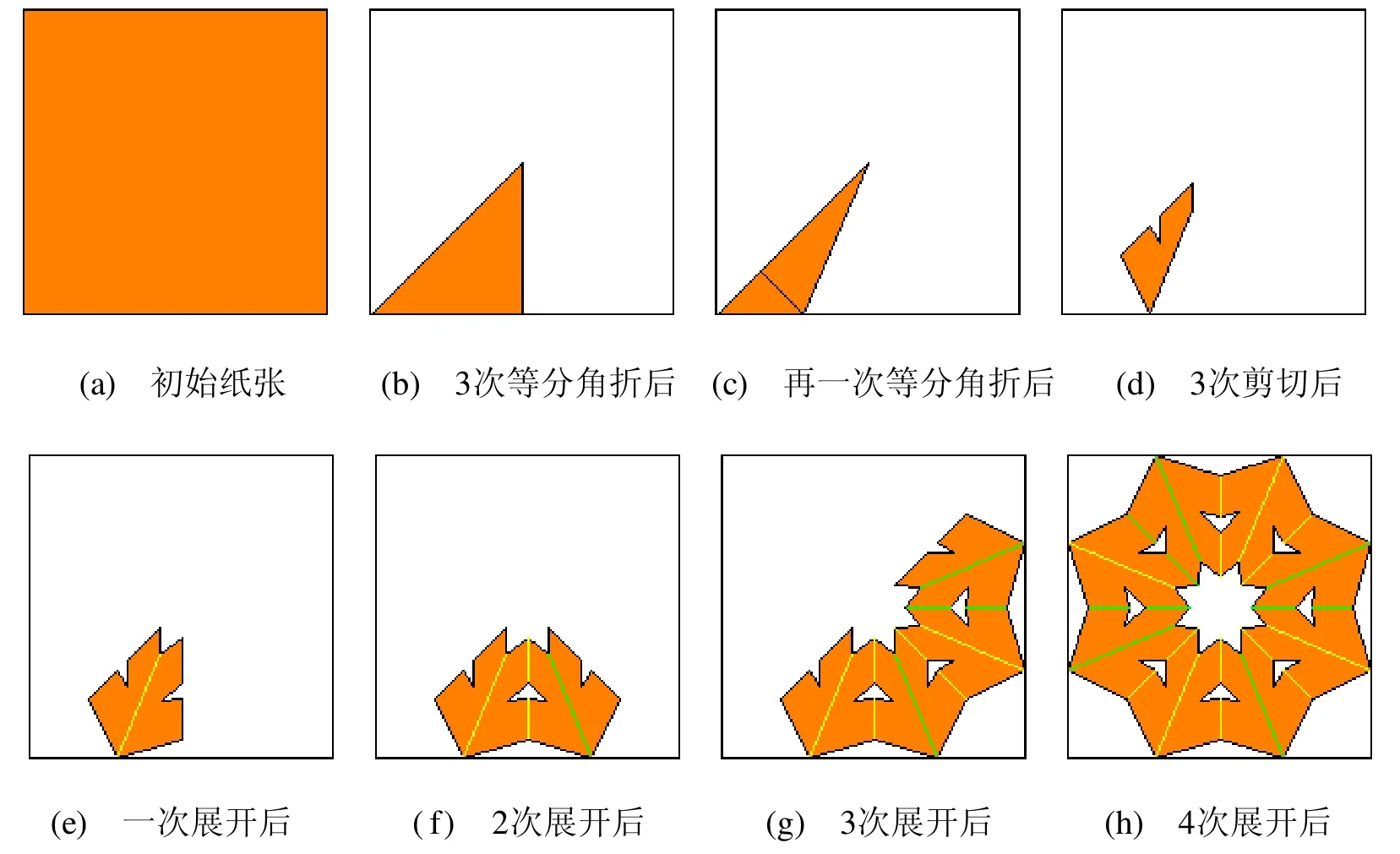
图4 折剪一个窗花的过程截图

5 结 论

与前人给出折纸计算模型相比[2-3,5]，本文给出的计算模型综合考虑了折叠、剪切和展开的计算，并且详细考虑了折痕的生成与表示。所开发的原型软件Virtual Paper验证了这个模型的可行性。

本文所提出的模型虽然是为计算机辅助儿童折纸和剪纸设计而设计的，但是它也可以应用在其他方面，如服装的裁剪方案设计。

进一步工作应重点放在如下2方面：一是进一步扩展该模型，使得它能够兼容非简单折叠；二是进一步完善Virtual Paper软件，使得它能够在三维空间以夸张的形式显示当前纸态并且能够以动画形式演示各种操作。

[1]禾 稼. 彩版儿童剪纸大全[M]. 长春: 吉林美术出版社, 2007. 1-342.

[2]Lang R J. A computational algorithm for origami design [C]//Proceedings of the 12th Annual ACM Symposium on Computational Geometry, Philadelphia,1996: 98-105.

[3]Ida T, Takahashi H, et al. Computational origami system Eos [C]//Proceedings of the 4th International Conference on Origami, Science, and Mathematics and Education, Pasadena, 2006: 69-73.

[4]Bern M, Hayes B. The complexity of flat origami [C]//Proceedings of the 7th Annual ACM-SIAM Symposium on Discrete Algorithms,Atlanta, 1996: 175-183.

[5]Kishi N, Fujji Y. Origami, folding paper over the web [C]//Proceedings of the 3rd Asian Pacific Conference on Computer and Human Interaction,Shonan Village Center, 1998: 337-342.

[6]Peng D, Sun S, Pan L. Research on Chinese paper-cut CAD system [C]//Proceedings of the 4th International Conference on Image and Graphics, Sichuan, 2007:892-896.

[7]张显全, 于金辉, 蒋凌琳, 等.计算机辅助生成剪纸形象[J]. 计算机辅助设计与图形学学报, 2005, 17(6):1378-1382.

[8]Mantyla M. An introduction to solid modeling [M].Rockville: Computer Science Press, 1988. 69-76.