中考数学复习要点指导

✿贵州省湄潭县石莲中学 李成康

如何把学生从“题海”中解放出来是历年来众多数学教师探索的一个重要课题.传统复习，教师往往把目标定位在“查缺补漏”上，因而呈现给学生的是支离破碎的题目.我认为高效的复习应突出知识间的联系与区别，形成知识体系.在复习时应搜集与课题有关的所有知识，把这些知识进行分类、有序、系统地进行整理、组合，把复习定位在“促进知识系统化”目标.这个收集、整理、组合的任务应该落在我们教师的肩上，以例题为载体，以基础知识为主干，落实知识的重组，使知识系统化.下面我就教师在总复习时如何精选例题与各位同行探讨.

一、例题覆盖面大，突出重点

选取例题要体现以下特点：①知识点覆盖面大，具有代表性、典型性；②既能突出考查蕴涵在它们中的数学思想和数学方法，又能反映“课程标准”中最主要而又最基本的要求.③内容背景新颖，具有多样性和时代感，力求“新”“精”.

比如在复习“实数”时，可选取如下例题：

例1：（2009年山东省济南市）2009年10月11日，第十一届全运会将在美丽的泉城济南召开.奥体中心由体育场，体育馆、游泳馆、网球馆，综合服务楼三组建筑组成，呈“三足鼎立”“东荷西柳”布局.建筑面积约为359800平方米，请用科学记数法表示建筑面积是（保留3个有效数字）（ ）.

分析：此例以当今的社会热点、国家大事为背景，包含的知识点比较多，覆盖面较大，也是现在中考命题的热点，它考查了近似数、有效数字、科学计数法，解决问题的难点是有效数字，可用口诀：“前面是零不算数，中末是零要数好.”

二、立足基础关注热点

教师要把握中考趋向，立足基础，关注热点.热点是什么？如应用型问题、实验操作、探究规律、方案设计、图形变换、读图识图等.热点只与题目形式有关，其基础是“不变量”.利用其题目形式激发学生的好奇心、求知欲，能有效地吸引学生的注意力，使学生诱发联想，抓住实质，就能起到以点带面、举一反三、触类旁通的作用.

例如在进行“探究规律性试题”的复习时，可选取如下例题：

例2：（2009年广西壮族自治区南宁市）正整数按下图的规律排列.请写出第20行，第21列的数字.

分析：此例是现在中考命题的热点，要猜想的结论往往需要从简单情况或者特殊情况入手进行归纳，通过观察、分析、综合、归纳、推理等一系列探究活动，发现规律，大胆猜想得出结论.这类例题有利于激发学生对数学现象的好奇心，培养学生的学习兴趣，帮助学生学会从数学的角度发现问题、提出问题，在解决问题的过程中学习思维策略，充分发挥自己的观察和猜想能力.

三、体现“三位一体”

在总复习时应立足课本，夯实双基，以课本为根，拓展为叶，这样才能更好地使用教材，吃透教材.通过对近几年中考试题的研究不难发现，课本是试题的基本来源，大多数试题都是在课本基础上组合、加工和发展的结果.因此，在中考复习选取例题时，要以课本为蓝本，以《中考说明》为导向，以2009年中考数学题为载体，体现“三位一体”，这样复习就能做到有基础、有方向、有新意，同时还要做到一题多用、推陈出新.

例如在进行“函数的图像”复习时，可选取如下例题：

例3：（2009年贵州省安顺市）如图，乌鸦口渴到处找水喝，它看到了一个装有水的瓶子，但水位较低，且瓶口又小，乌鸦喝不着水，沉思一会后，聪明的乌鸦衔来一个个小石子放入瓶中，水位上升后，乌鸦喝到了水.在这则乌鸦喝水的故事中，从乌鸦看到瓶的那刻起开始计时并设时间为x，瓶中水位的高度为y，下列图像中最符合故事情景的是：（ ）.

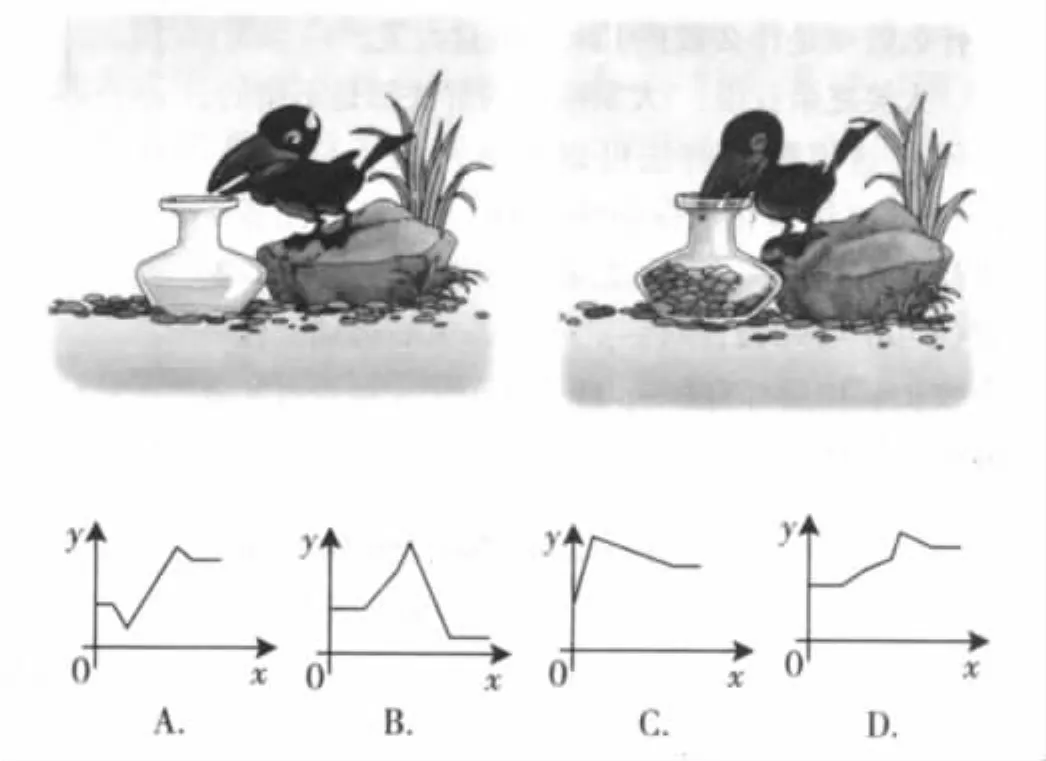
分析：此例是考查函数图像的应用，它来源于课本，但有一定的变式，又是《中考说明》必考的内容之一，解题时，只要弄清题意，把握好关键词，能读图、识图，在图像中理解文字的表达，这样问题就迎刃而解了.

又如在复习“三角形的角”这一部分时，可选取如下例题：

例4：（2009年山东省枣庄市）如下图，将一副三角板叠放在一起，使直角顶点重合于O点，则∠AOC+∠DOB= .

分析：此例是考查三角形的基础知识，是《中考说明》的必考内容之一，学生可以自己利用两块同样的三角板进行平移、旋转、翻折等变换，其实质是两个直角的度数相加，从而得出问题结论.

四、解题注重通法

如何解数学题？数学家G·波利亚提出了4个阶段：即弄清问题、拟定计划、实现计划和回顾。这就是说，数学解题是从理解问题开始，经过探索思路，转换问题直至解决问题，进行回顾的全过程的思维活动。现在的中考题越来越淡化技能技巧，注重通性通法的考查，功能是选拔性的考试，能够继续在高中学习，试题形式和素材千变万化，但其中蕴涵的数学思想和数学方法往往是相通的、不变的，因此，师生的解题思路要能突出解题的通用解法、常规解法，同时体现例题的“应用性”.

比如在复习“一元二次方程的应用”时，可选取以下例题：

例5：（2009年山东省青海市）在一幅长为80cm，宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边，制成一幅矩形挂图，如下图所示，如果要使整个挂图的面积是5400cm2，设金色纸边的宽为xcm，那么x满足的方程是（ ）.

分析：此例是“一题多变”、“一图多变”的好题，其解题思路是把“金色纸边”矩形的长、宽，表示出来，构建“一元二次方程模型”迎刃而解.

例6：（2009年天津市）注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路填空，并完成本题解答的全过程.如果你选用其他的解题方案，此时，不必填空，只需按照解答题的一般要求，进行解答即可.

如图①，要设计一幅宽20cm，长30cm的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2∶3，如果要使所有彩条所占面积为原矩形图案面积的，应如何设计每个彩条的宽度？

由横、竖彩条的宽度比为2∶3，可设每个横彩条的宽为3x，则每个竖彩条的宽为.为更好地寻找题目中的等量关系，将横、竖彩条分别集中，原问题转化为如图②的情况，得到矩形ABCD.

结合以上分析完成填空：如图②，用含x的代数式表示：AB=____cm，AD=____cm；矩形ABCD的面积为cm2；

列出方程并完成本题解答.

分析：此例的解答是用数形结合思想，以寻找矩形的长、宽为切入点，并涉及代数式的表示、一元二次方程及其解法等知识.题目中给出的“分析”为问题的解答作了铺垫，从而降低了问题的起始难度，有利于不同层次的学生解答问题.

这些例题融于图形，突出了对数形结合思想方法的考查，有利于发展学生的思维，培养学生的创新意识，激发学生的兴趣.在教学中应强调学生掌握解此类题的通性通法，便于学生理解知识的重点，摆脱“题海战”之苦，同时也能唤起学生探究事物发展变化的好奇心，开拓学生的视野.

总之，总复习既要圆满完成大容量、大跨度的复习任务，又要能体现“新”授课的特色.在中考数学总复习选取例题时，教师只有跳进“题海”精选例题，并对精选的例题进行适当剖析、演变、深化，以点带面，学生才能跳出“题海”，使总复习达到“以少胜多”“事半功倍”的效果.俗话说：“陈饭抄了吃，只要佐料好，味道会更美！”