自适应遗传神经网络模型（IAGA－BP）及其在坝体结构损伤识别中的应用

郭永刚，潘城荣

(1.中国水利水电科学研究院，北京100044；2.北京工业大学建筑工程学院，北京100124)

0 引言

遗传神经网络模型在坝体结构损伤识别领域是一种有效的方法，已取得了很多成果[1]。然而，基本遗传算法(Simple Genetic Algorithm,SGA)易出现早熟收敛，同时存在随机漫游、稳定性不佳、收敛速度慢等问题。

针对以上缺点，本文对SGA提出改进措施，对其中的编码、遗传算子进行改进，引入改进的自适应交叉变异算子，并利用经改进的自适应遗传算法（Improved Adaptive Genetic Algorithms,IAGA）优化误差反向传播神经网络 （Back Propagation Neural Networks,BPNN）的权值，建立了经改进的自适应遗传神经网络（IAGA-BP）模型，并将该模型应用于大坝的结构损伤识别。结果表明，IAGA-BP模型在全局收敛能力、收敛精度等方面与基本遗传神经网络模型SGA-BP相比有显著提高。

1 遗传神经网络基本原理

遗传算法（GA）与神经网络（NN）的结合机制是根据GA解空间遍及整个搜索空间的特性，从随机解集中，遗传算法可以得出一定范围内的优化解，以此形成NN网络的连接权值，再由NN按负梯度方向进行快速搜索，以达到全局最优解。这样做，既可保证收敛的全局最优解，又能保证收敛的速度。神经网络采用广泛使用的BP网络，包括输入层、隐层、输出层，根据定理：假定BP网络隐层单元可以根据需要自由设定，那么一个三层网络可以实现以任意精度近似任何连续函数[2]。神经元的激活函数采用S型函数。

2 遗传神经网络的学习步骤[3]

2.1 编码并形成初始种群

随机产生一组分布，对该组中的每个权值和阈值按特定的编码规则进行编码，进而构造出初始种群，其中每个个体代表一种神经网络。

2.2 提供学习样本

学习样本也就是当前神经网络的理论输入和期望输出值。

2.3 适应度评价

将网络误差函数（能量函数）的倒数作为适应度函数。种群个体经过适应度函数评价后，接下来就可以进行遗传操作了。

2.4 遗传操作

（1）选择算子：可采用的选择方法包括轮盘赌选择法、排序选择法、随机竞赛选择法、最优保存策略选择法等。

（2）交叉算子：常用的交叉算子包括单点交叉、两点交叉、一致交叉等。

（3）变异算子：常用的变异算子包括均匀变异和非均匀变异。

遗传神经网络的学习流程图见图1。

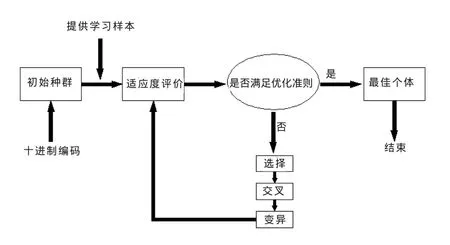
图1 遗传神经网络的学习流程图Fig.1 The flow chart of GA-BP

3 基本遗传算法（SGA）的改进

3.1 编码：采用十进制编码

SGA采用二进制编码，计算时须进行编码及解码操作，计算效率下降，并在此过程中引入了量化误差，降低了精度。在对神经网络的权值和阈值编码时，如采用十进制实数编码，就可以大大减小种群中个体的长度，也可避免因采用有限位数二进制编码近似代替实数所带来的误差[4]。

3.2 自适应交叉和变异算子

对遗传算法的收敛性起决定作用的是交叉和变异算子[5]。在SGA中，交叉概率常随机地选取一个较大的值，而变异概率选取一个较小的值，通常交叉概率选为 0.5～1.0， 变异概率的取值范围是0.001～0.05，这带有很大的盲目性。采用固定的交叉概率、随机配对的方式进行配对后交叉，在遗传算法前期，优秀基因有可能得不到保留就会被替代，这样影响遗传算法的收敛速度，有可能使种群发散；在后期，由于优胜劣汰，只有少量的优良个体生存，造成种群局部收敛[6]。为此，为了避免发散和陷入局部收敛，要保持种群中“好”的个体，需要自适应地调整pc和pm。这可以通过对高适值的解降低pc和pm的值、对低适值的解提高pc和pm的值来实现，以使高适值的解加快GA收敛的同时，低适值的解防止GA陷入局部极小。

一种评价收敛的方法是观察fmax-当种群收敛时fmax-较低，把fmax-作为衡量一个种群是否收敛的标尺。pc，pm和fmax-的值成反比，如下式所示：

其中fmax为种群个体适应度最大值；f为种群个体平均适应度值；k1，k2≤1.0。

上述方法可以较有效地避免局部收敛和种群发散，但是交叉和变异概率不取决于个别特殊解，种群所有解的交叉变异概率值一样，拥有高适应度值和低适应度值的解交叉变异概率相同。按照上述方法，种群接近全局收敛时，fmax-f值降低，交叉和变异概率提高，这将导致即将全局收敛的解被破坏，最终导致全局无法收敛。

鉴于上述缺点，应该寻求方法保护这些高适应度解，比如可以降低高适应度解的交叉变异概率值，提高低适应度解的相应值。由于高适应度解有助于种群的全局收敛而低适应度解的存在可以防止种群局部收敛，因此，变异概率不仅和fmax-有关，还与解本身的适应度f值有关，f和fmax越接近，变异概率越低。同样，交叉概率和fmax-f＇有关，f＇为被选择成为交叉父代的较大适应度值。改进的方法公式如下：

其中 k1，k2≤1.0。 当 f'=时，pc＝k1。 同理，f=时， pm＝k2。 但是，当 f'＜，f＜时，pc和 pm有可能超过1。为了避免这种情况发生，做如下限制：

其中 k3，k4≤1.0。

改进后，当解的适应度值最大时，交叉和变异概率都为0，一个种群中适应度值最高的优秀个体就能被成功传递到下一代。虽然有上述优点，但是此改进结合选择操作，适应度值高的解将成指数增长，最终可能导致早熟收敛。为克服这个缺点，在自适应遗传算法中为每个解引入一个默认的变异概率（0.005）。

下面讨论 k1，k2，k3，k4的取值问题。为方便起见，pc和pm的方程表示如下：

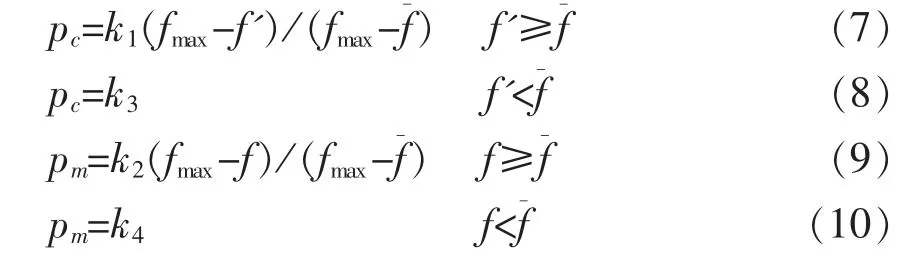
遗传算法文献很好地证明了取适当大的pc（0.5＜pc＜1.0）和适当小的 pm（0.5＜pm＜1.0）有助于遗传算法的收敛[7]，适当大的pc可以获得广泛的种群信息而适当小的pm可以防止解的破坏。但如果pc和pm不变，则种群易陷入局部收敛。改进的目的是防止遗传算法陷入局部收敛。为实现这一目的，用适应度值低于平均值的解来搜索包含全局最优解的解空间，这些低于平均值的解应该被破坏（变异），因此使 k4=0.5。同样，适应度值等于平均值 f的解也应该被破坏，因此也使k2=0.5。同样的原因，使k1，k3=1.0，这将保证适应度值低于或等于适应度平均值的解被交叉。当被选择成为交叉父代的个体中适应度值较大者 （f＇）趋近于种群适应度最大值fmax时，由公式（7）可知 pc逐渐减小，当 f＇增加到等于 fmax时，pc=0.0。

个体的交叉和变异概率应该是个体本身适应度值的函数，而基本遗传算法（SGA）中 pc和 pm是不变的，这就缺乏种群搜索过程中pc和pm的动态性，这也是SGA的局限所在。D.Whitley也提出了一种自适应遗传算法[8]，与本文自适应遗传算法（IAGA）相比，两种算法都旨在不影响收敛性能的前提下保持种群的多样性。但是，Whitley方法中自适应变异概率应用于遗传算法稳定的背景，而本文的自适应遗传算法（IAGA）侧重于种群世代的更替；Whitley的方法奉行的是群体精英策略（Populationary Elitism），所以这种方法没必要保护优秀种群，与其不同的是，本文的自适应遗传算法明确保护最优解；另外，两种方法的自适应原则也不一样：Whitley方法的自适应变异概率和海明距离（Hamming Distance）有关，而本文自适应遗传算法的交叉和变异概率和个体的适应度值有关。

4 IAGA－BP模型的建立及在大坝损伤识别中的应用

4.1 数值算例

一混凝土重力坝，坝高H=180 m，上游坡面垂直，下游坡面倾斜系数m=0.75。坝基长度上游取1.5H，下游取2H，坝基深度取2H。坝体混凝土的弹性模量 E=2.85×1010Pa， 泊松比为 v=0.167，密度为 2 400 kg／m3， 张开剪切传递系数为 0.3，抗拉强度 ft=1.96×106Pa，抗压强度 fc=22×106Pa。基岩弹性模量 E=2.0×1010Pa，泊松比 v=0.3，密度为 2 600 kg／m3。

计算采用以下基本假定：（1）坝体和坝基连续，即坝体和坝基之间紧密联系在一起；（2）坝体和坝基的材料是均匀的；（3）基岩材料为线弹性材料。

大坝示意图见图2。

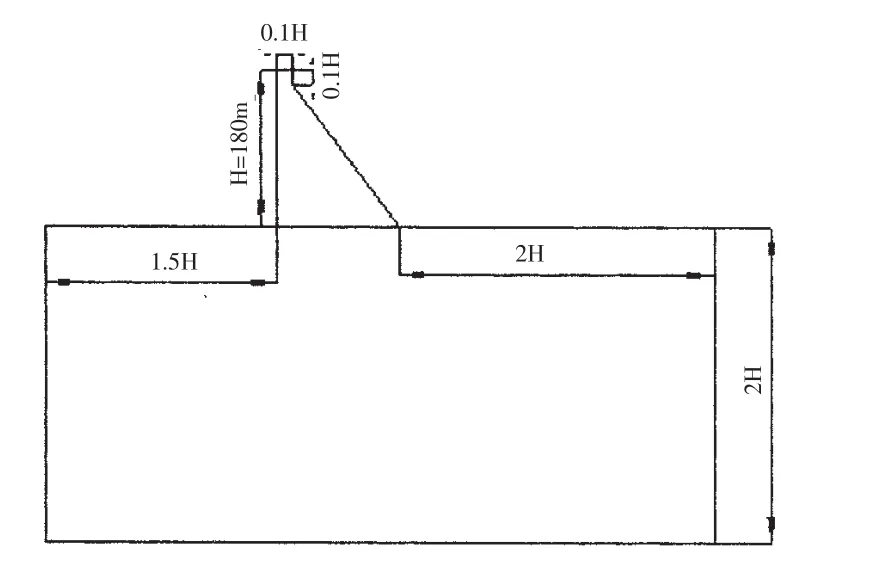
图2 水库大坝示意图Fig.2 Sketch of the dam

4.2 IAGA－BP模型的建立及应用

固有频率是模态参数中最容易获得的一个参数，而且识别精度高。本文运用ANSYS建立坝体模型，选取第3、5、7单元三种损伤工况（分别用A、B、C表示，并用下标1～9表示单元损伤10%～90%），用单元的刚度折减模拟损伤，通过这一原理假定三个单元分别损伤5%、15%、25%、35%、45%和50%。经模态分析，取坝体前十阶频率与完好坝体固有频率相对变化率ΔF（即坝体频率变化）作为改进自适应遗传神经网络（IAGA-BP）的输入参数，而输出参数设为两个：1代表有损伤，0代表无损伤。选取三个单元分别损伤20%、40%、60%、80%、90%的前五阶频率变化作为模型的检测样本。至此，IAGA-BP模型建立完成。本文同时建立了SGA-BP模型，模型的形式和输入与IAGA-BP模型相同。分析结果如下，其中，图3～图5为ANSYS建立的坝体模型三种损伤工况；表1为检测样本；表2和图6分别为两种模型的检测结果对比分析表和拟合效果对比图。

图3 损伤工况1Fig.3 Dam damage operating model 1

从图6和表2可以看出，与SGA-BP模型相比，除了A2、B9和C6三种损伤有相对较大的误差外，IAGA-BP模型的拟合效果理想，基本接近全局收敛，能有效识别出损伤的位置，而SGA-BP模型的拟合效果较差，误差明显较大；IAGA-BP模型的实际输出和理论输出更为接近，精度更高，理论与实际输出差值最大仅为0.116 5，而SGA-BP模型的最大差值达到了0.276 2；另外，IAGA-BP模型的收敛速度明显更快，在迭代61次时就趋于稳定，接近全局最优解。

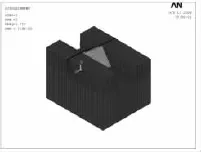
图4 损伤工况2Fig.4 Dam damage operating model 2

图5 损伤工况3Fig.5 Dam damage operating model 3

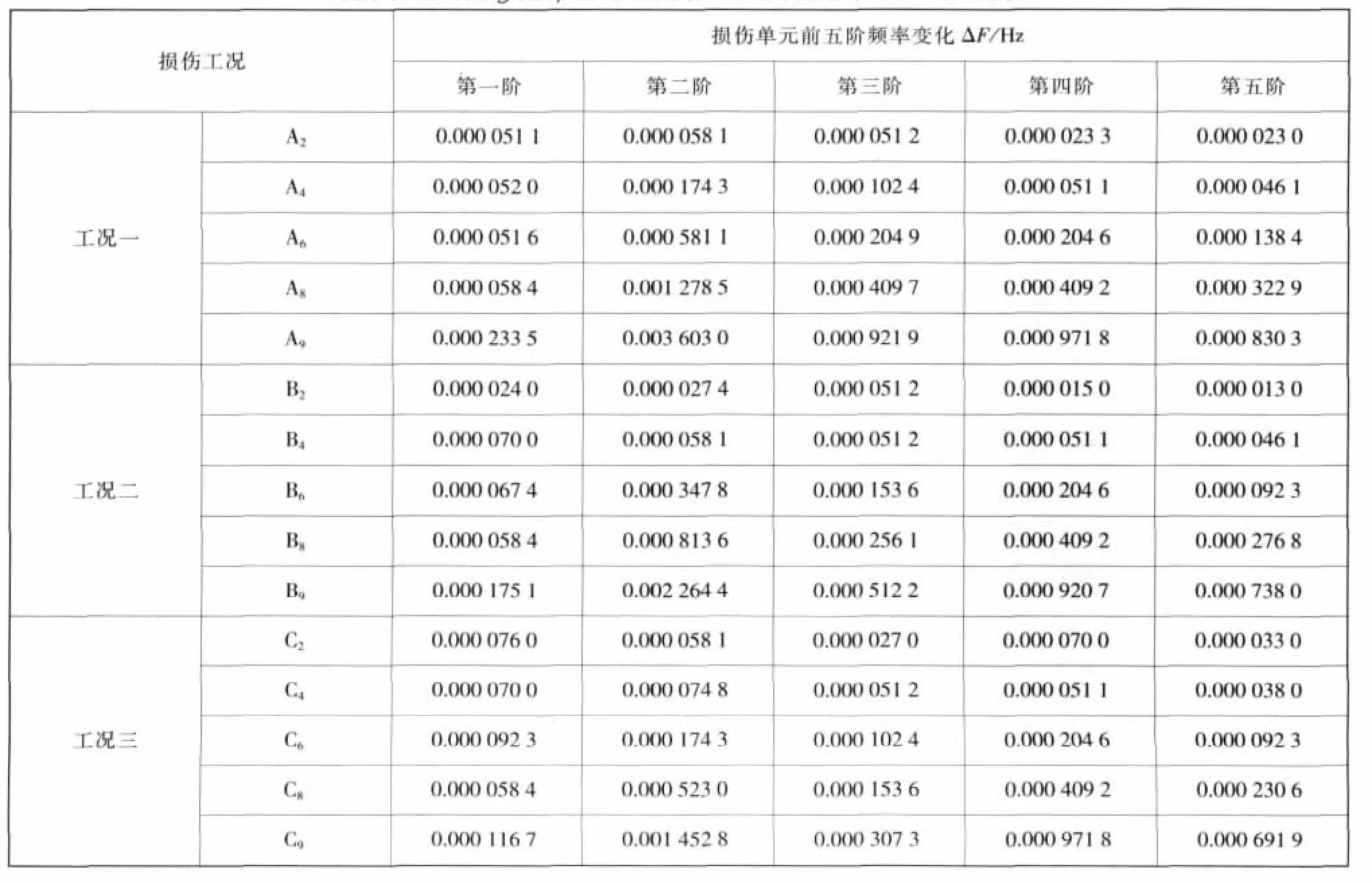
表1 SGA－BP模型和IAGA－BP模型检测样本Table 1 :The testing samples for the SGA-BP model and IAGA-BP model

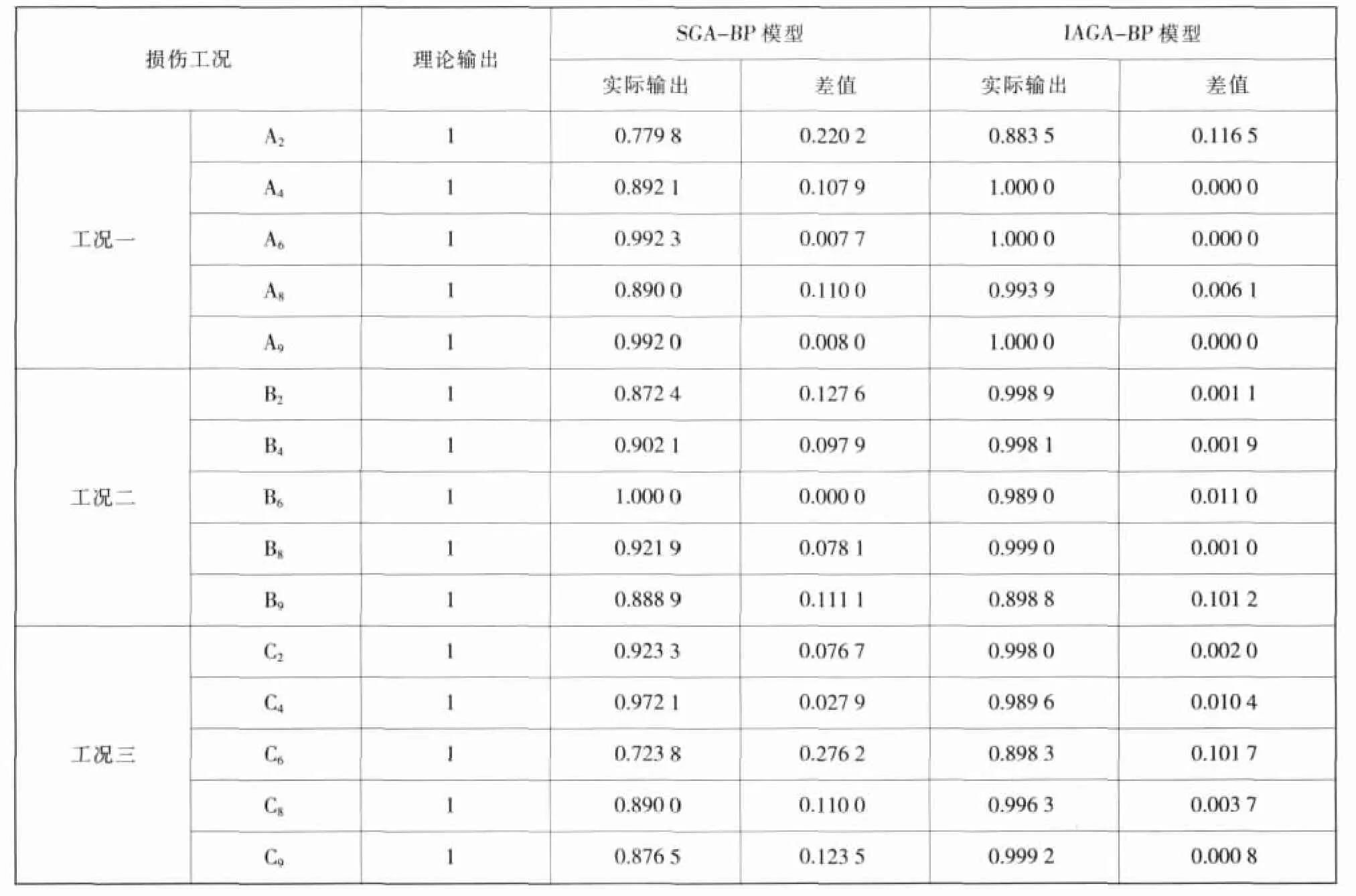
表2 SGA－BP模型和IAGA－BP模型检测结果对比分析表Table 2 :Comparison of the analysis results between the SGA-BP model and the IAGA-BP model

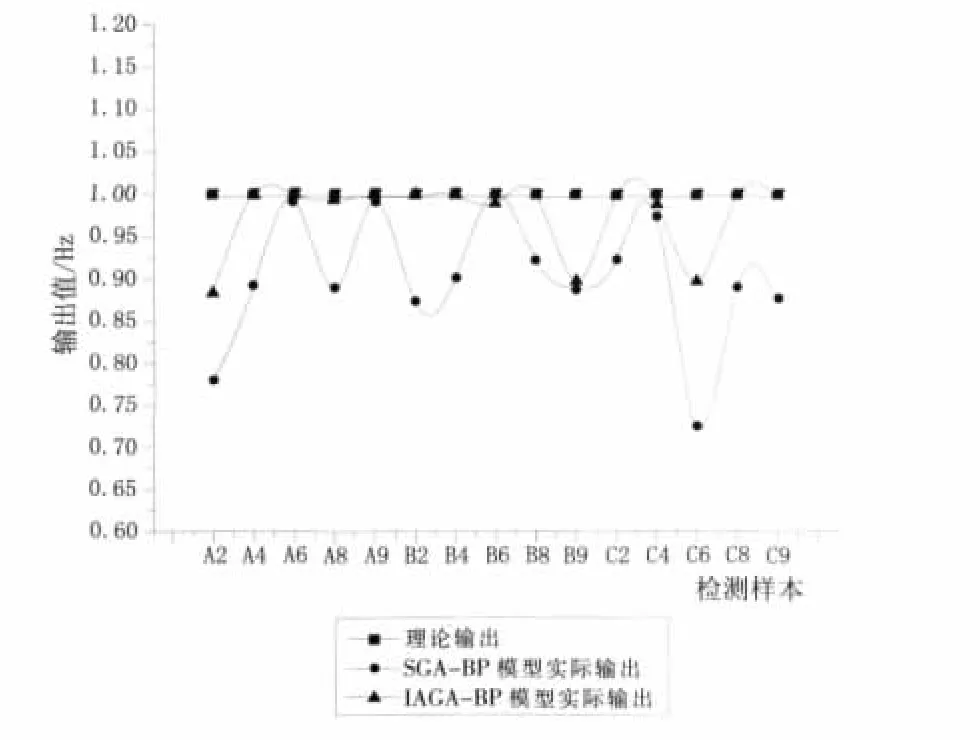
图6 两种模型理论与实际输出对比Fig.6 Comparison between theoretic values and actual values

经分析，由于引入了自适应交叉和变异算子，使得IAGA-BP模型的学习具有自适应性，交叉和变异概率随着种群的变化动态地调整，始终处于一个种群既不局部收敛、又不发散的适当值，最终达到全局最优解，收敛精度高。但是由于用于训练的神经网络的参数设置问题，以及训练样本数量稍显不足，可能导致了模型A2、B9和C6三种损伤的误差。SGA-BP模型之所以误差太大，是因为该模型中的pc和pm是不变的：pc和pm取值太大，容易破坏种群最优解，最终可能导致种群发散，无法收敛；取值太小，种群易陷入局部收敛，导致精度大大降低。

文献[8]也对遗传神经网络在坝体结构损伤识别中的应用进行了研究，该文献利用基本遗传算法优化神经网络权值并建立了模型，同时将其运用于坝体结构损伤识别[9]。该模型与SGA-BP模型相比，其改进之处在于遗传算法采用的是浮点编码。从该文献的试验结果可以看出，其建立的模型在收敛速度方面较为理想，而个别工况精度欠佳，识别误差较大。据笔者分析，该模型有如下不足：检测样本只用到三种损伤工况十阶频率的后五阶频率，训练样本数量偏少，会影响训练学习效果；同时，检测样本只用到三种工况的三种损伤类型，虽然检测效果相对理想，但是不具普遍性。总体而言，该文献所提出的模型只能在一定程度识别坝体结构损伤。

为便于比较，本文引用文献[8]的算例建立坝体的有限元模型。除了引入自适应算子大大增大了模型的全局收敛能力外，本模型优于文献[8]的模型还在于其不仅用到坝体三种损伤工况前十阶频率的后五阶，还加入了前五阶频率，使本文模型有丰富的训练样本，提高了训练效果和自适应性；另外，为充分检验经训练后模型的普遍性，本文取每种工况五种损伤形式的后五阶频率组成模型的检测样本。通过对两者检测分析结果的比较可以看出，本文所建立的自适应遗传神经网络模型（IAGA-BP）无论在全局收敛能力、收敛精度方面都优于前者。

5 结语

本文针对基本遗传算法（SGA）收敛速度慢、计算稳定性差、效率低下等问题，提出一种经改进的自适应遗传算法（IAGA），采用十进制编码，从而建立了自适应遗传神经网络模型 （IAGABP）。将此模型运用于坝体结构损伤识别并与基本遗传神经网络模型（SGA-BP）以及文献[8]所建立的模型对比，试验结果表明IAGA-BP模型具有以下优势：

（1）收敛精度较高，具有较强的全局收敛能力。由于引入自适应交叉变异算子，交叉和变异概率始终处于一个有利于种群全局收敛的适当值，克服了SGA-BP模型易陷入局部收敛和种群发散的缺点。

（2）收敛速度明显加快，在迭代61次时就趋于稳定，接近全局最优解。

但对用于训练的BP网络参数设置问题缺乏深入的研究，以及训练样本数量相对不够丰富，导致了IAGA-BP模型在个别单元的损伤定位上有误差，这部分有待进一步完善。

总体上，本文提出的IAGA-BP模型可以较好地对一般小型混凝土重力坝进行损伤定位。另外，还可将该方法用于结构的模态参数识别。

[1]梁化楼,戴贵亮.人工神经网络与遗传算法的结合:进展及展望[J].电子学报,1995,10(10):195～198.

[2]杨健刚.人工神经网络使用教程[M].杭州:浙江大学出版社,2001.

[3]王志旺,张保军.大坝变形监测遗传神经网络模型[J].岩土力学,2003,24(增 1):130～133.

[4]赵振勇,王力,王保华,等.遗传算法改进策略的研究[J].计算机应用,2006,12(26):189～192.

[5]Srinivas M.Genetic algorithms:A survey[J].Computer,1994,26(6):17～26.

[6]杨照选,贺建民,周晓兰.一种改进的遗传算法解决旅行商问题[J].解放军理工大学学报（自然科学版）,2004,5(5):30～33.

[7]陈国良.遗传算法及其应用[M].北京:人民邮电出版社,1996.

[8]D.Whitley and D.Starkweather.GenitorⅡ-A distributed genetic algorithm.J.Expt.Theor.Artif.Int,2:189～214,1990.

[9]李小荣,郭永刚.基于遗传算法优化神经网络权值的大坝结构损伤识别[J].震灾防御技术，2008，3(2):189～196.