一种应用于多重化逆变的变压器研究

胡亮 胡绪昌 王铁军

（1. 海军工程大学电气与信息工程学院，武汉 430033；2 江苏江阴 63680 部队，江苏 214431）

1 引言

多重化逆变器是基于“移相多重叠加”原理，通过大量电力电子器件的应用来实现逆变。所以其高次谐波污染不可避免。降低开关频率和减少开关器件的运用是解决这一问题的途径之一。传统的“移相”方式，是通过控制开关器件，在时间上创造相位差角。本文考虑在逆变器中加入新型变压器，在空间上创造相位差角，来降低开关频率和减少开关器件应用。

变压器是利用电磁感应原理，以交变磁场为媒介，把初级绕组从电源吸收的某种电压的交流电电能转变成另一种电压的交流电能，由次级绕组向负载提供。除自耦变压器外，一般变压器的初级与次级绕组之间只有磁耦合而没有电路上的直接联系。其主要作用是改变电压幅值[1]。而文献2中打破传统观念提出了任意相变成三相的滤波变压器，它不仅可以改变电压幅值，还可以变换相数和消除谐波。其中滤波的基本理论方法也是“移相多重叠加法”，基本叠加方式是初级磁合成与次级电压合成，相对应的铁心结构形式是三相铁心与多相铁心。体积和重量都较大，铁心材料利用率也不高。所以本文提出了一种与多相异步电动机定子铁心结构相似的新型滤波变压器铁心结构来解决传统铁心这些的问题。使其能够应用于多重化逆变器中。

2 新型变压器原理

2.1 移相多重叠加技术

本文的基本理论是“移相多重叠加法” ，其基本思想是将N个输出电压（或电流）为方波的逆变器依次移开一个相同的相位角，然后通过变压器进行初级磁合成或次级电压（或电流）合成，使方波中的某些谐波的相位相反，并得到阶梯波改善输出波形。该理论广泛用于多相整流[3-6]，有源逆变[7-9]，消除谐波，改善波形[10]等方面。针对该方法的应用研究还有大量文献记载，此处仅对其进行简要说明。

2.2 新型叠加变压器的结构

文献 11中将变压器与异步电动机做了详细比较，指出了两者在工作原理和电磁关系上的相似之处。所以本文提出的新型变压器铁心结构类似于多相异步电机的定子铁心。文献12中提出了用于六相异步电动机的电抗器，并通过仿真分析证明其滤波效果明显。本文中则将其绕线形式引入变压器中，并将铁心结构设计成为形如感应电机定子，12个孔型槽均匀分布于铁心上，绕组线圈绕于孔型槽中(具体图形如图1)。

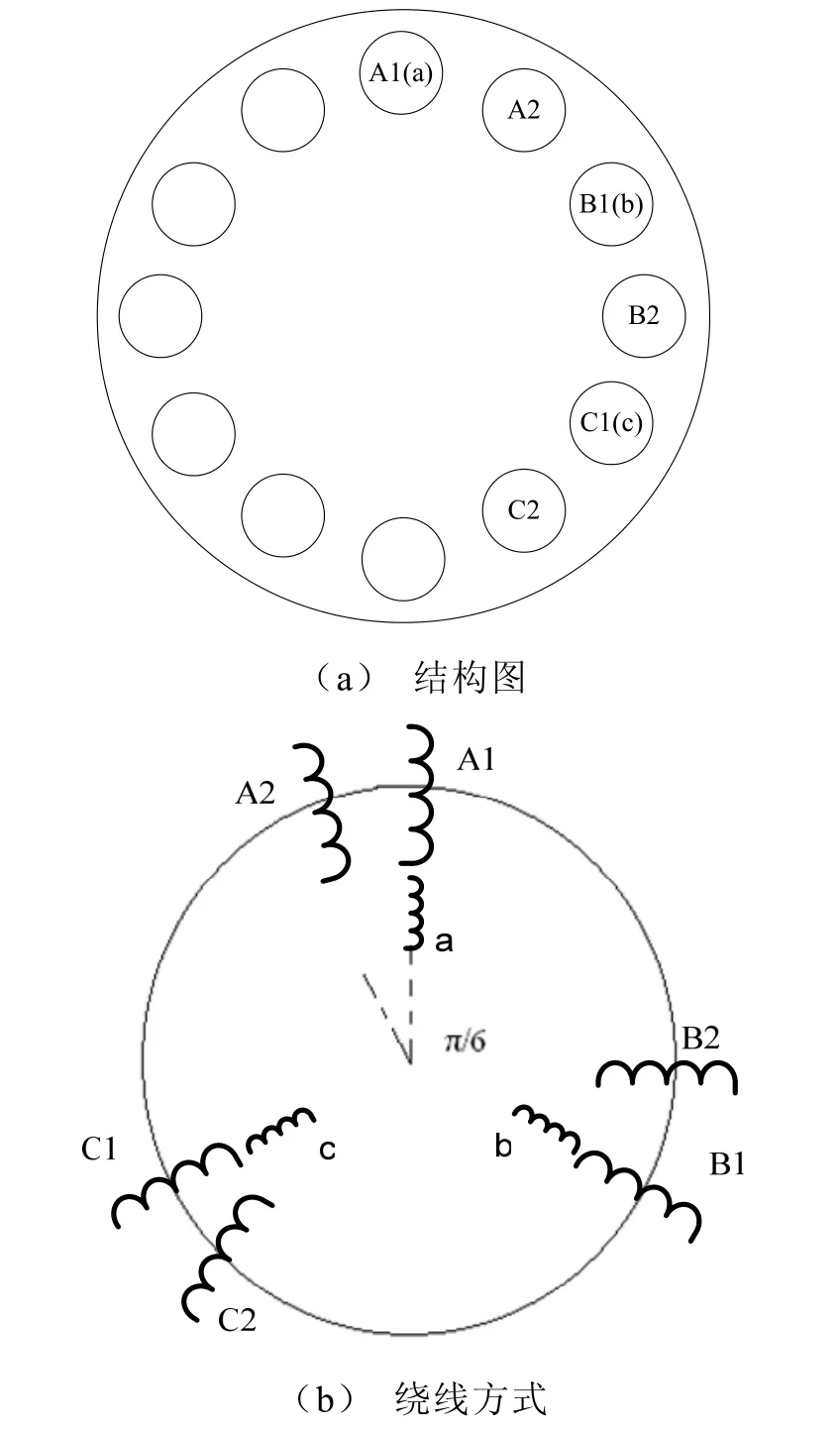
图1 结构图与绕线方式

由图1（b）可见，绕组线圈A1、B1、C1与A2、B2、C2分别为两套三相输入绕组，它们之间相差π/6的相位角。线圈a、b、c为输出绕组，与第一套输入绕组（A1、B1、C1）布置于同一孔槽中。输入端电压来自三相方波逆变器，输出端供给三相负载用电。方波逆变器、新型变压器、三相负载的连接关系图如图2。

图2 连接关系图

2.3 叠加变压器滤波原理

直流电源通过三相桥式方波逆变器，得到三相方波电压，并联连接两套三相输入绕组并通过输入绕组在新型叠加变压器中进行磁动势叠加（具体结构如图3）。下面对变压器中的磁动势进行分析。三相方波电压产生的磁动势中，含有基波磁动势和高次谐波磁动势，以第一套绕组的A1相轴线为空间坐标原点，并以 A1相绕组电流为零的瞬间作为时间轴的起点。

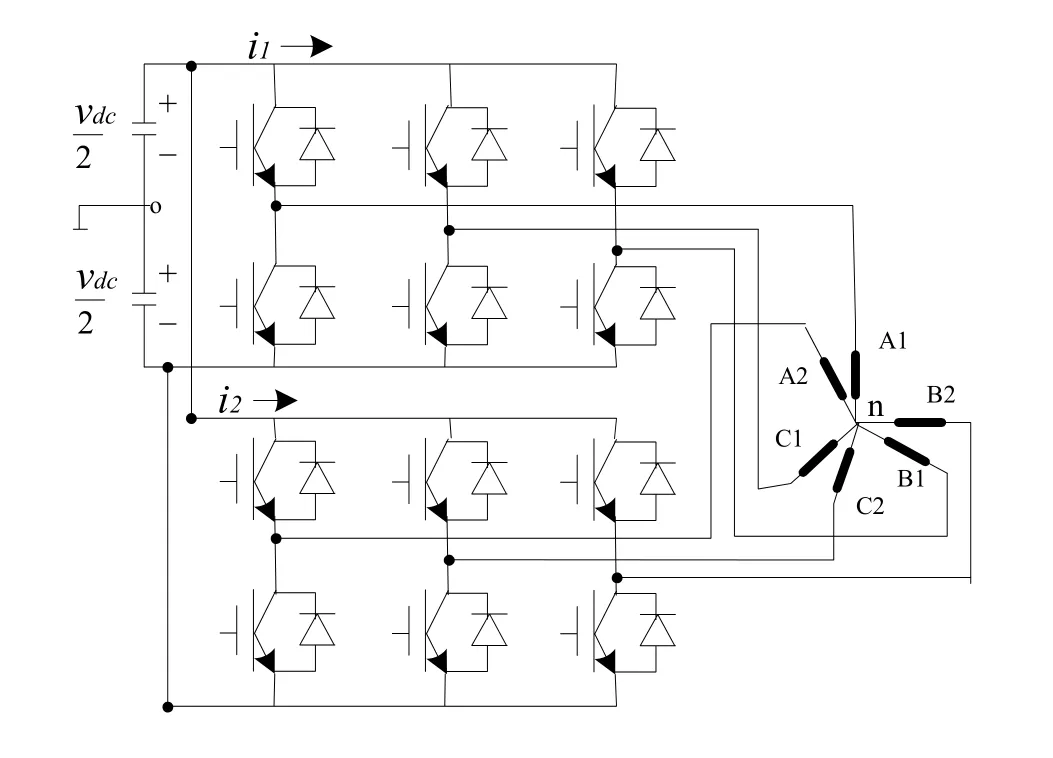
图3 三相逆变桥

基波磁动势：第一套输入绕组所产生的基波磁动势是与感应电机定子磁动势相似的波幅恒定不变的旋转波，其式为

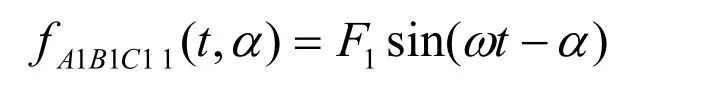
F1为基波磁动势幅值。ω为旋转磁场的频率。由于第二套输入绕组电压幅值、频率与第一套绕组相同，但空间上与第一套绕组相差 π/6相位角。则其产生的基波磁动势可表示为

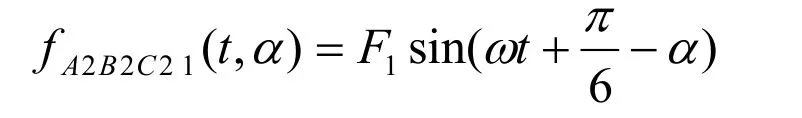
高次谐波：（1）3次谐波磁动势：由于每套输入绕组的三相之间的对称性3次谐波磁动势得以消除。（2）5次谐波磁动势：第一套绕组产生的 5次磁动势可表示为 FA1B1C15(t,α)=F5sin(ωt+5α)。第二套绕组产生的 5次磁动势为 FA2B2C25(t, α)=F5sin[ωt+5(α+π/6)]。为分析方便设时间为初始，即ωt=0。合成的5次谐波磁动势为

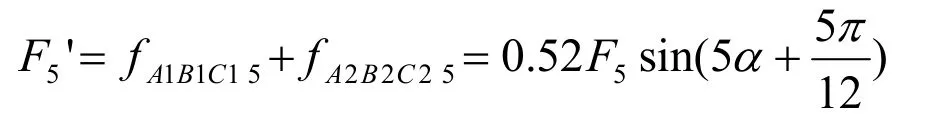
（3）7次谐波磁动势：第一套绕组产生的7次磁动势表示为 FA1B1C17(t, α)=F7sin（ωt-7α），第二套绕组产生的 7次磁动势表示为 FA2B2C27(t,α)=F7sin[ωt-7(α+π/6)]。合成 7 次谐波磁动势为

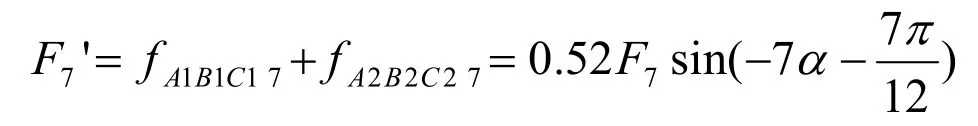
图4以5次谐波磁动势为例做向量图。由图可见，在新型变压器中，高次谐波磁动势得以明显削弱，起到了滤波作用。

3 系统的数学模型与仿真分析

3.1 数学模型

在分析该新型变压器数学模型时，做如下假设：

（1）忽略滤波变压器的漏电抗和绕组电阻。

（2）三相输出为平衡的电阻性负载。

（3）处于同一槽内的绕组相互漏感忽略。

（3）磁路为线性，铁心的涡流、饱和、磁滞损耗不予计算。

变压器电压方程即可表示为如下式的矩阵形式

电压向量

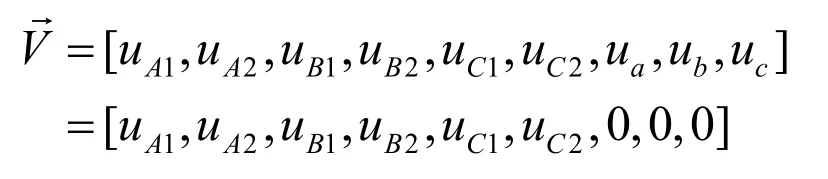
电流向量

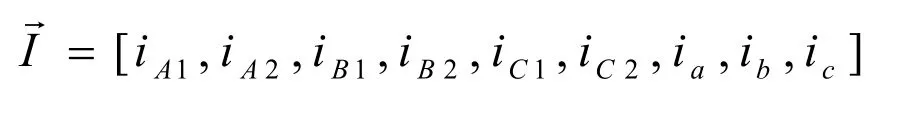
电阻矩阵

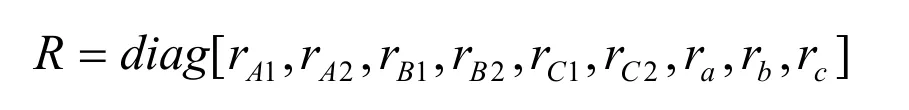
电抗矩阵LC模仿六相感应电机系统的电抗矩阵可表示为

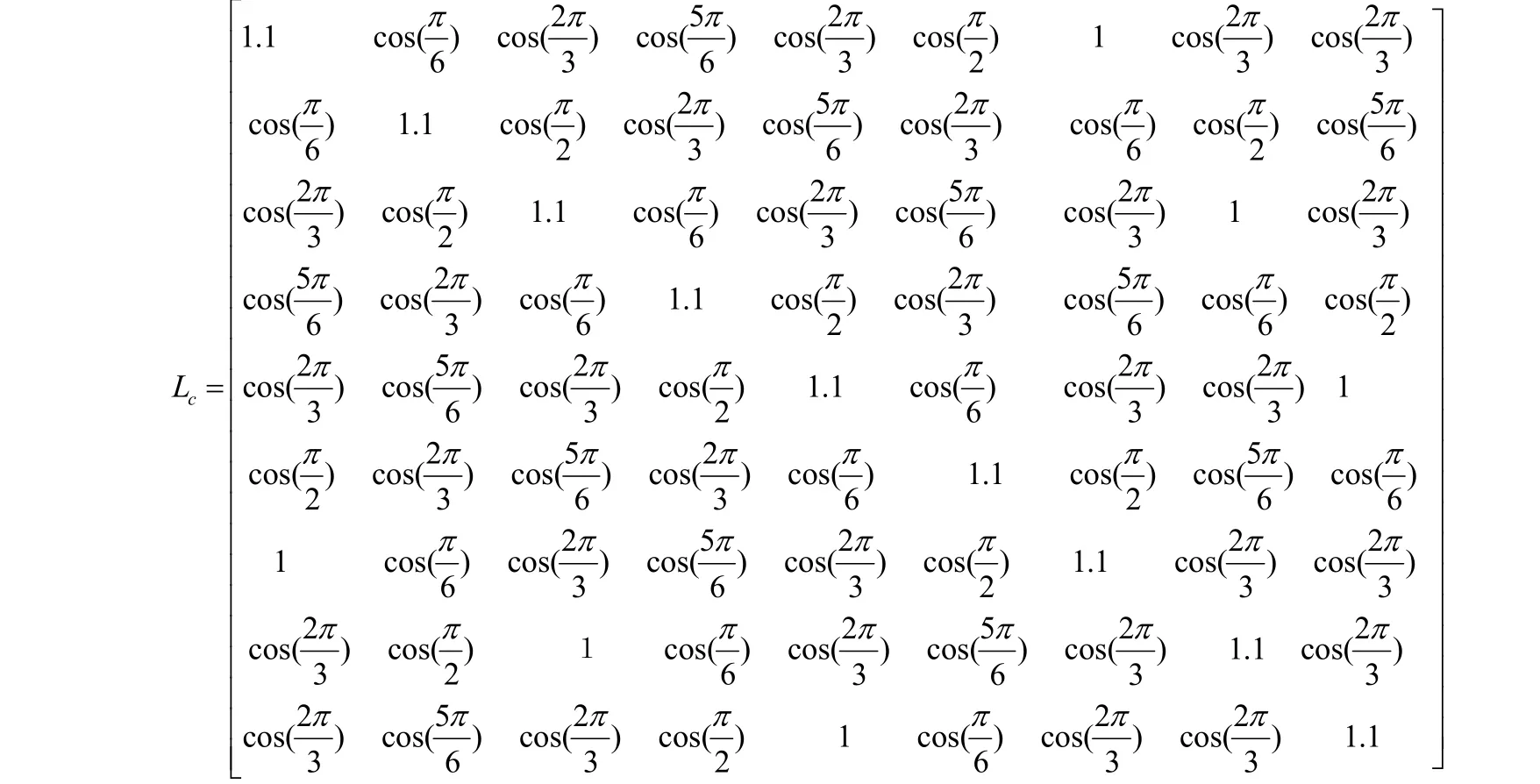
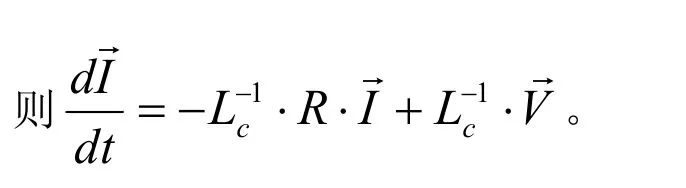
3.2 仿真及结果

输入三相方波逆变器的波形如图 5。经过新型叠加变压器后的电流波形与频谱如图6所示。

图4 向量叠加图

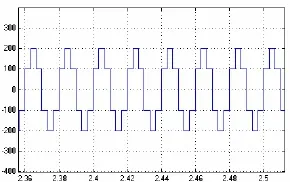
图5 输入波形图

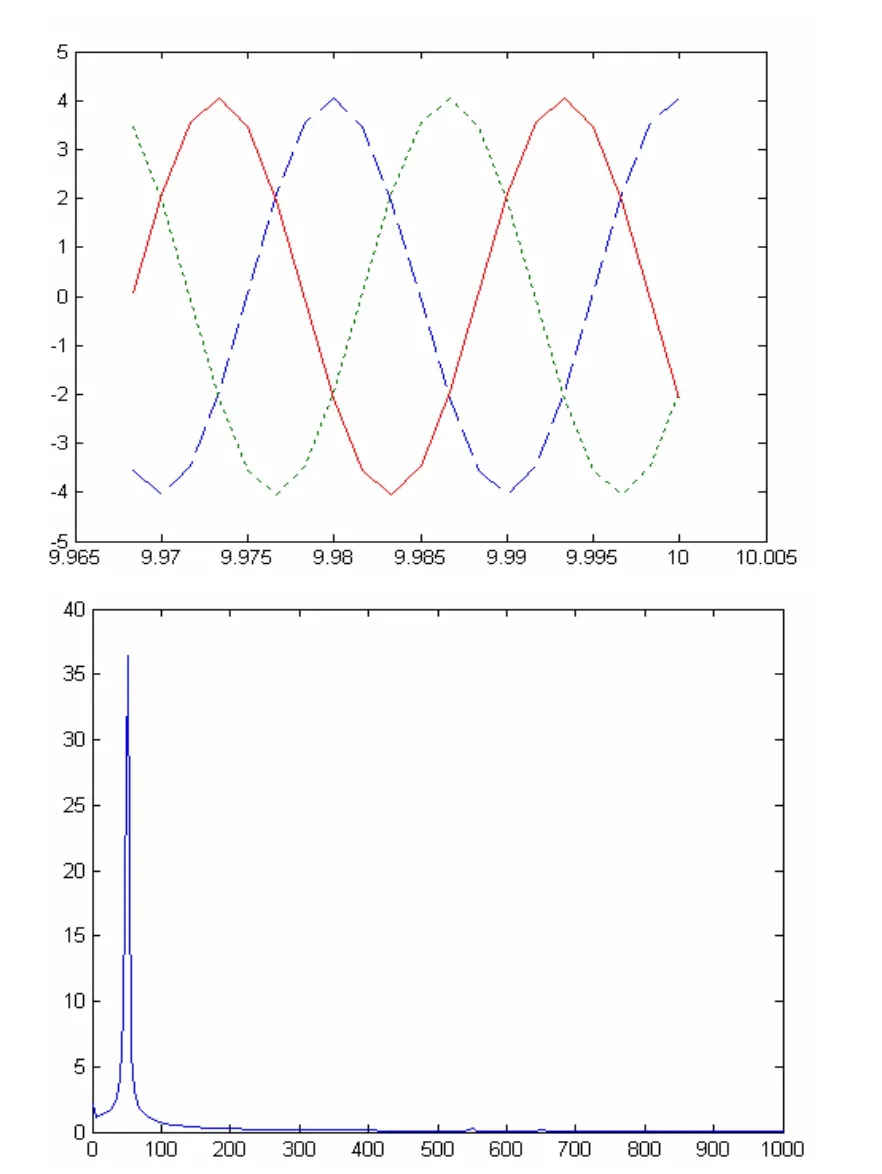
图6 输出电流波形与频谱图

由图可看出方波电压在进过叠加变压器后的电流波形非常接近正弦波，由频谱分析可知本结构对3、5、7次谐波抑制效果明显。

4 结论

本文基于多重叠加的基本原理，在前人基础上提出了一种新型变压器的铁心结构，简单的三相方波逆变器通过该结构进行初级磁叠加，高次谐波在叠加过程中基本被抑制。本文利用simulink仿真软件，对其建模并且仿真，仿真结果与理论分析基本一致。但由于在建模之初进行了简化假设，在实验中会遇到很多问题，比如磁路饱和、漏磁通的计算等问题。如何解决这些问题还需要进一步分析和研究。

[1]张植保. 变压器原理与应用[M]. 北京： 化学工业出版社, 2003.

[2]刘凤君. 任意相变成三相的滤波电源变压器. 航天科技报告, HT-920179, 1992.

[3]屈克庆, 靳希, 董立骏等. 基于载波移相技术的PWM 多重化整流器[J]. 上海电力学院学报, 2008,(3)： 282-285.

[4]罗隆福, 肖华, 李勇. 基于新型换流变压器的 12相整流和谐波分析[J]. 电力系统及其自动化学报.2006, 18(6)： 26-31.

[5]刘凯,李明勇.多相整流谐波抑制技术[J].船电技术,2005(3)：26-29.

[6]王凤翔, 张涛, 白浩然. 采用移相电抗器的多相整流系统[J]. 沈阳工业大学学报, 2008, (4)： 361-365.

[7]郑书路, 王明彦. 有源逆变器的电流型移相多重叠加并联运行分析[J]. 电力电子技术, 2008, (2)：13-17.

[8]Byung-Moon Han,Seung-Taek Baek Young-Soo Jon.New configuration of 36-pulse voltage source converter with auxiliary circuit[J]. Electrical Engineering, 2006, ( 88)： 497-507.

[9]付超, 石新春, 王毅. 级联型逆变器的空间矢量移相调制方法[J]. 电力电子技术, 2005(10)：51-53.

[10]王凤翔, 耿大勇. 移相电抗器对变流器供电系统谐波抑制的机理研究[J]. 中国电机工程学报, 2003, (2)：54-57.

[11]黄小玲. 异步电动机与变压器的比较[J]. 今日科苑,2008, (14)： 68.

[12]王铁军, 辜承林, 赵镜红等. 一种用于抑制多相异步电动机定子谐波电流电抗器的研究[J]. 电工技术学报, 2006, (10)： 1-6.