基于自适应Backstepping方法的舰船电力系统混沌控制
蔡亮 周涛
(江苏海事职业技术学院电气工程系,南京 212000)
1 引言
舰船电力系统是一个非线性、强耦合、多变量的高阶复杂系统,而非线性系统在一定参数条件下会进入混沌状态。对于电力系统来说,混沌现象的发生,会表现为一种非周期性的,似乎是无规则的、突发性或阵发性的机电振荡。现有研究表明混沌运动有可能作为电力系统扰动失稳过程的一个中间阶段而存在[1-2]。在舰船的航行中,电机员多次在电力系统运行中观测记录到了这种振荡,这对舰船电网的安全运行构成了潜在的威胁,可能导致系统失稳[3-4]。因此,对舰船电力系统进行混沌研究有非常大的实际意义。
目前,电力系统的混沌研究主要针对于陆上电力系统,而舰船电力系统较陆上电力系统有容量小,线路短,工作环境湿度大等特点[5]。不同于陆上电力系统,有关舰船电力系统混沌研究仍处于起步阶段,以理论分析和仿真研究为主。在有关舰船电力系统混沌现象的研究中,文献[3]、[4]深入研究了舰船电力系统的双机并联运行的工况,经过变换得到了一个适合分析舰船电力系统混沌运动的模型。文献[5]研究舰船电力系统运动状态随参数改变的过程,文献[6]中利用Melnikov和Lyapunov指数这两种方法作为判据,对两机并联舰船电力系统的混沌现象进行数值分析,结合系统的功率谱分析,提高了分析系统发生混沌振荡的准确性,指出当发电机之间存在功率传递和受到一定幅值的周期性负载扰动时,舰船电力系统将出现混沌振荡。对于混沌现象的控制,理论研究中已有大量的控制方法,并不一定能够直接应用于工程实际中的混沌系统。本文在文献[4]给出的双机并联运行舰船电力系统混沌运动的模型以及文献[6]对混沌现象的数值分析基础之上,采用Backstepping自适应控制方法,能够将混沌系统中的任意的不稳定点控制到该混沌系统的平衡点上。通过数字仿真,表明了该控制方法的有效性。
2 舰船电力系统混沌模型
[4]所提供的两台发电机并联运行时,形成的发电机互联系统。其基本供电网络结构可等效表示成图 1。其中, E1∠ δ1和E2∠δ2分别为系统中的两台发电机电动势,和分别代表两台发电机的同步电抗, xl和 rl为分别是线路电阻和电抗,由于舰船电力系统中线路短,故线路电阻非常小,常忽略不计,P,Q表示系统负荷。
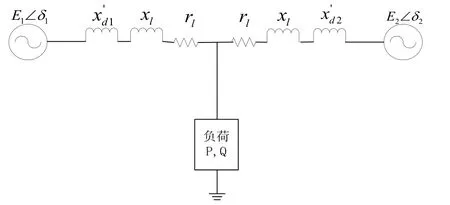
图1 两机并联模型
考虑发电机参数相同的情形,并记δ=δ1-δ2,ω=ω1-ω2为两台等值发电机的相对功角和相对功角速度。则两机互联系统具有以下形式:
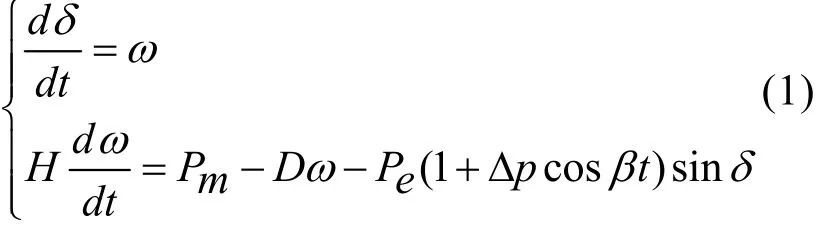
式中,H、D为等值转动惯量和等值阻尼系数;Pm为发电机输入机械功率, Pe为系统输出的电磁功率。 Δ p⋅ pec os βt 是为了研究船舰电力系统在扰动下混沌运动而引入的电磁扰动,其中Δ p⋅ pe表示扰动的幅值,β表示扰动的频率。
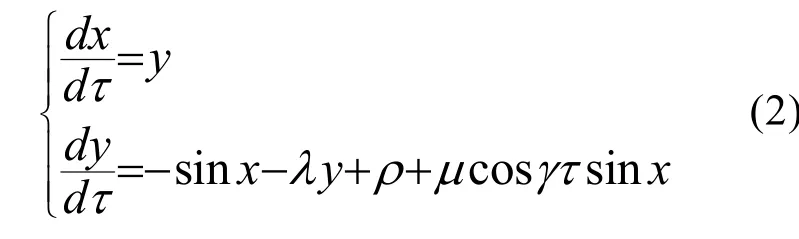
3 采用自适应Backstepping舰船电力系统混沌的控制
这里所说的自适应Backstepping方法是指利用Backstepping方法设计一个自适应控制器,当系统已经处于混沌运动,该控制器能够将任意的不稳定点控制到该混沌系统的平衡点上,能够达到迅速抑制混沌的目的。这里针对舰船电力系统的混沌运动来设计控制器,根据自适应Backstepping的设计方法[7],引入一个控制输入u加入到状态方程(2)中,如式(3)所示:

由(3)式中的第一个方程,为了使V1( x)= x2/2的导函数负定,特为y设计稳定化函数α1(x)。假设α1(x)= - k1x( k1>0)并定义以下误差变量

为了设计简单,不妨设 k1= 1 ,则于是有关于的方程组

定义Lyapunov函数
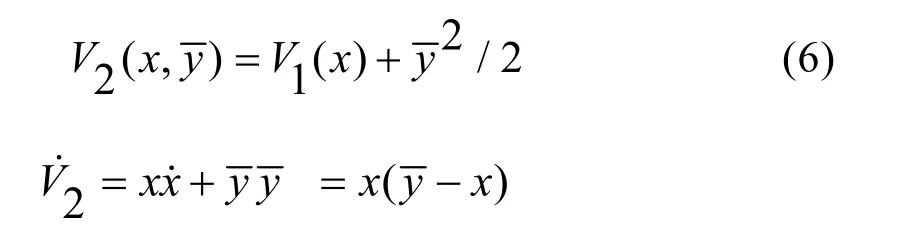
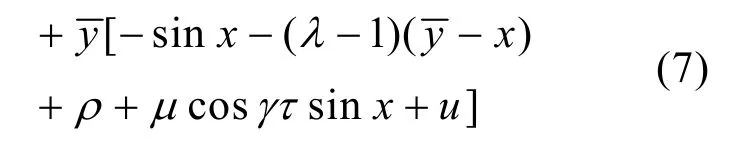
若
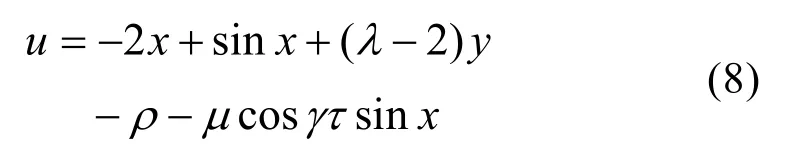
若扰动幅值μ为未知参数,利用μˆ作为μ的参数估计,向其逼近,控制器应为:
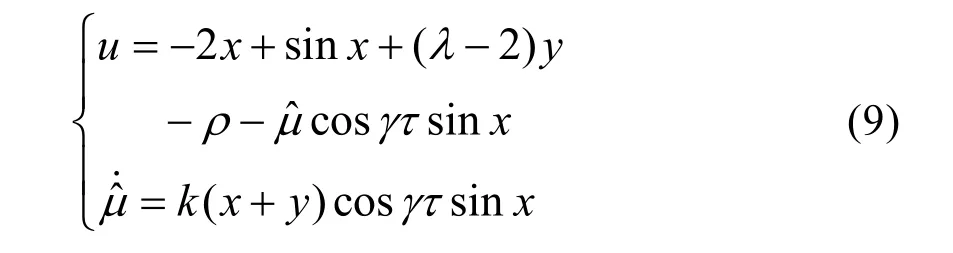
式中 k > 0 ,可以调节自适应律的速度。
加入控制器,则舰船电力系统的状态方程为
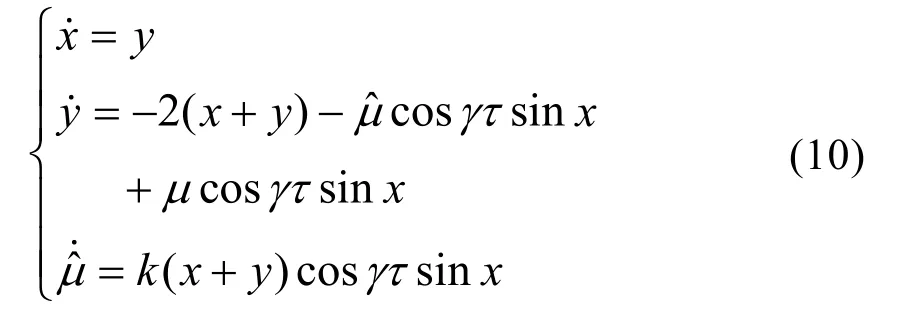
变换得
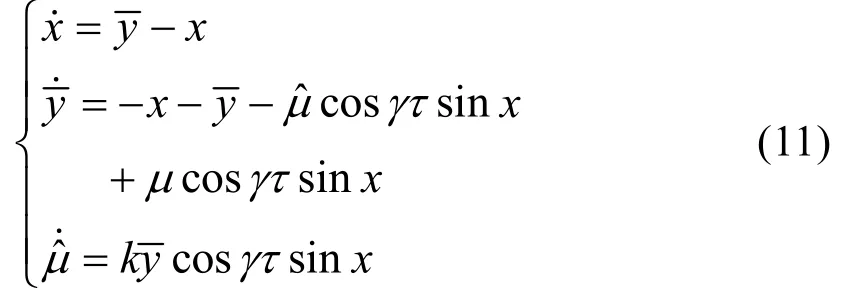
为证明在控制器(9)的作用下,系统是渐进稳定的,取Lyapunov函数:

4 数字仿真
由舰船电力系统混沌运动的数值分析,得到在参数λ=0.4,ρ=0.2,扰动频率γ=0.8的情况下,当扰动幅值μ=1.3时,系统处于混沌状态[6]。为了抑制混沌,引入控制器(9),在系统处于混沌状态运行100s后,投入控制器,受控系统的动态相应及相图如图2、图3、图4、图5所示。
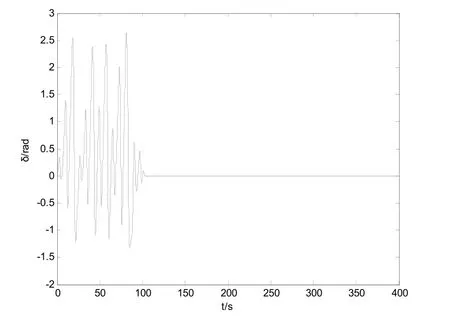
图2 功角δ的变化曲线 扰动幅值µ =1.3
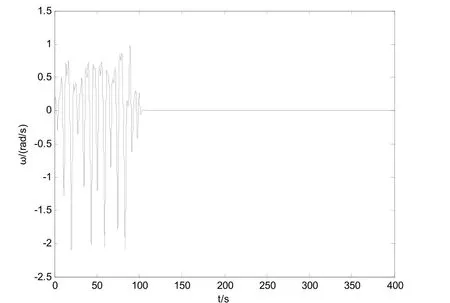
图3 功角速度ω的变化曲线扰 动幅值µ=1.3
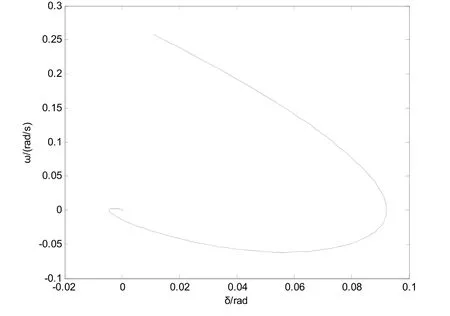
图4 功角δ和功角速度ω相图扰动幅值µ=1.3
从图2功角δ的变化曲线和图3功角速度ω的变化曲线可以看出,在控制器作用下,舰船电力系统的混沌运动得到了迅速的抑制,且回到了平衡点。图4功角δ和功角速度ω相图也显示了这一点。图5μˆ-1.3的变化曲线反映了受控系统能够很好辨识系统的幅值,但是存在一定的误差,从仿真的过程来看,其误差的大小与k的选取有关。不过,实验的目的在于能够抑制舰船电力系统的混沌运动,从仿真的效果来看,无疑达到了目的,说明了自适应Backstepping方法在控制系统混沌的有效性。
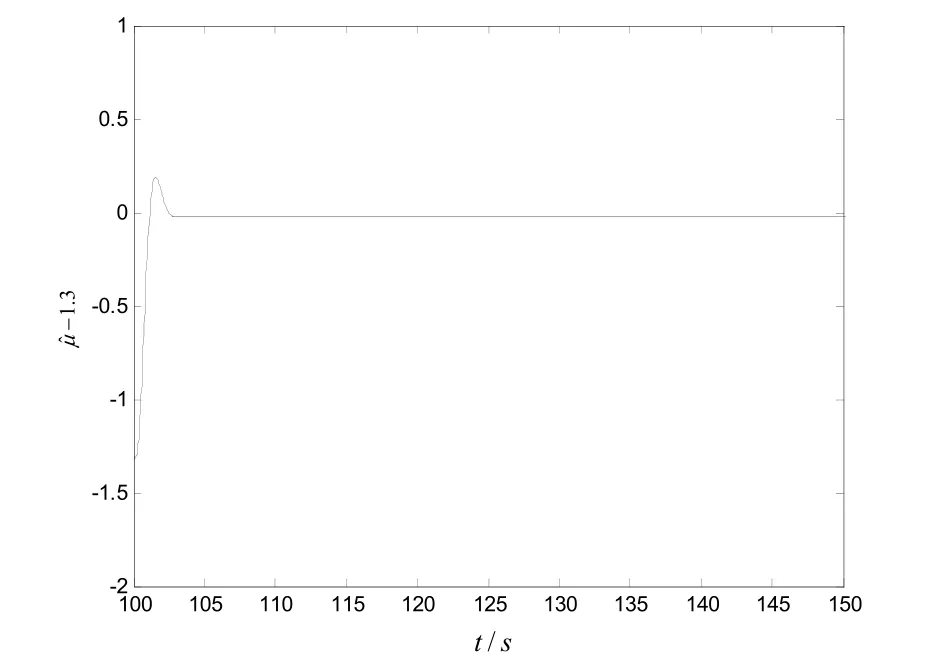
图5 μˆ-1.3的变化曲线
5 结束语
本文运用自适应Backstepping方法分别对舰船电力系统的混沌运动进行了控制。实现了系统已经处于混沌运动,投入控制器,使系统稳定到混沌系统的平衡点,同时还保证该系统的全局稳定性。能够达到迅速抑制混沌的目的。
参考文献:
[1]张强. 电力系统非线性振荡研究[J]. 电力自动化设备. 2002, 22(5): 17-19.
[2]贾宏杰,余贻鑫,王成山. 电力系统混沌现象及相关研究[J]. 中国电机工程学报, 2001, 21(7): 26-30.
[3]施伟锋. 关于舰船电力系统研究的一些探索[D]上海:上海海事大学, 2005.
[4]黄健. 船舶电力系统混沌现象研究[D]. 上海:上海海事大学, 2005.
[5]刘金波. 舰船电力系统暂态稳定性分析[D]. 哈尔滨:哈尔滨工程大学, 2002.
[6]蔡立勇. 舰船电力系统混沌运动的数值分析[J]. 船舶工程.2008, 30(3): 53-56.
[7]武玉强,李洪亮,孙海龙. 基于 Backstepping方法的多变量系统自适应控制[J]. 控制与决策, 2001:93-96.

